【数据结构】初步认识--树(基本概念、属性、实现方法)二叉树(种类)

目录

认识：树

树的一些名词

树的属性

树的实现

认识二叉树

各种二叉树

严格二叉树：

完全二叉树：

完美二叉树：

平衡二叉树：

二叉树的保存方式

动态创建节点

数组实现完全二叉树

---

P25-P26笔记，视频地址👇

http://www.bilibili.com/video/BV1Fv4y1f7T1?p=26&vd_source=02dfd57080e8f31bc9c4a323c13dd49c

认识：树

还记得我的数据结构第一站对于数据结构的简单导言么？

在日常生活中，为了组织不同类型的数据，我们需要不同类型的结构，帮助我们更高效更方便的找到想要的数据。

在我们以往的数据结构学习中，我们所接触到的都是一些线性的数据结构：数组，链表，栈，队列这些都是线性结构。而今天要学习的是树——经常用来表示层次数据的一种数据结构。

就像这样👇

像是倒着的树(弹幕也有小伙伴说更像树根hh)

树这种数据结构可以被定义为:链接在一起的被称为节点的实体的集合，用来模拟层级结构。 

有一些树(组织层次化数据)的应用我们是很常见的：电脑上的文件和文件夹(这个好亲切)；组织数据，方便快速搜索查询(后面会讨论的二叉搜索树)；还有一种特殊的Trie树，用来存储字典，实现动态拼写检查......

树的一些名词

接下来是一些树这种数据结构的词汇：

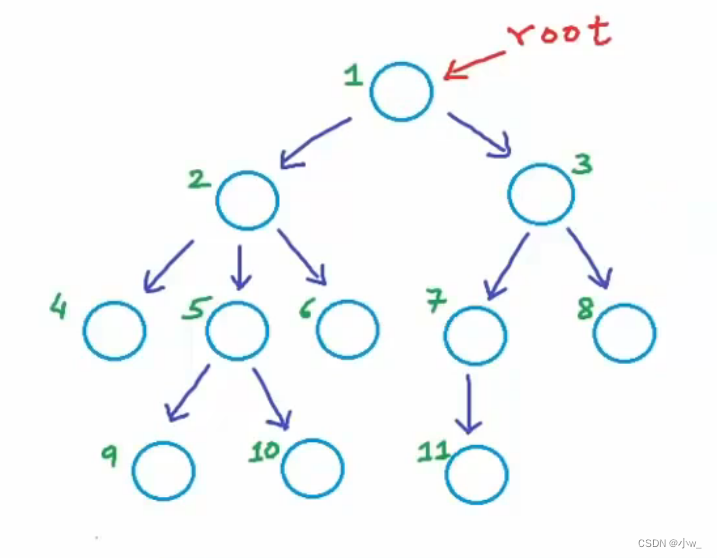
标好的顺序只是为了方便读者明确所指的是哪些节点，并不代表其他。

每个节点中可以存储任何类型的数据。

一个节点通过箭头向下链接到其他节点(单向链接)，那么这些被链接到的节点称为该节点的孩子/子节点，该节点称为其子节点的双亲节点。eg:图中1号节点是2、3的双亲结点，2号节点是4、5、6的双亲结点......

树的最顶部的节点是根节点，只有根节点没有双亲节点。1号节点是根节点没有双亲。

同一双亲的节点称为兄弟节点(sibling)。图中2、3号为兄弟节点，4、5、6号为兄弟节点......

树中所有没有孩子的节点称为叶子节点。4、6、8、9、10、11号都是叶子节点

至少有一个孩子的节点称为内部节点。1、2、3、5、7号节点是内部节点。

由于这些链接都是单向的，所以遍历树的时候只能单向遍历。

还有一些诸如：共同祖先啦、子孙、祖父母之类的这些概念和我们本身的认知是相符合的，就不再一一列出来啦。祖先：只要在该节点之上的都可以称为祖先。

父母不同、祖父母相同称为堂兄弟。(分的不怎么清写一下hh)

树的属性

1.递归。树可以被称为一个递归的数据结构。树递归可以理解为由一个树根和一些子树构成。如下图

递归就是通过调用自身来解决问题  

2.如果一棵树有N个节点，那么就会有N-1个链接。除了根节点，每个节点都有一个传入链接(边/箭头)。

3.树的高度和深度。

一个节点的深度就是从根节点到该节点的路径长度，也就是箭头个数。

根节点的深度定义为0.(好像国内定义为1 我这里就按老师讲的了，原理应该是一致的)

一个节点的高度就是从该节点到一个叶子节点的最长路径。叶子节点的高度为0.

树的高度也就是根节点的高度。

我的理解是：一个节点的长度是向上看，高度是向下看。

树的实现

树最常见的实现方式就是动态创建的节点，就像链表一样。主要以二叉树为例。

如上图右侧，每个节点包含三个位置：中间表示 存放的数据，左侧存放左孩的地址，右侧存放右孩地址。是不是感觉很亲切呀hh。这种只适用于二叉树哦

认识二叉树

不同场景中我们会使用不同类型的树，最简单最常见的具备这种属性的树就是任何节点最多包含两个孩子的二叉树。这也是我们主要讨论的。

二叉树最多只能有两个孩子，当一个节点只有一个孩子的时候，另一个孩子我们可以称为NULL，而对于叶子节点，我们可以说他的两个孩子都是NULL 

各种二叉树

严格二叉树：

                     满足每个节点都是0个或2个孩子

完全二叉树：

                     如果一棵树除了最后一层没有被填满其他层都被完全填充，并且所有节点都向左对齐，那么称为完全二叉树。最后一层没被填满的话，必须向左对齐。

这里向左对齐的意思是：完全二叉树的最后一层如果没有被填满，那么所有的节点都必须是左孩子，不能有右孩子。如果有一个节点只有右孩子而没有左孩子，那么这个树就不是完全二叉树。

 

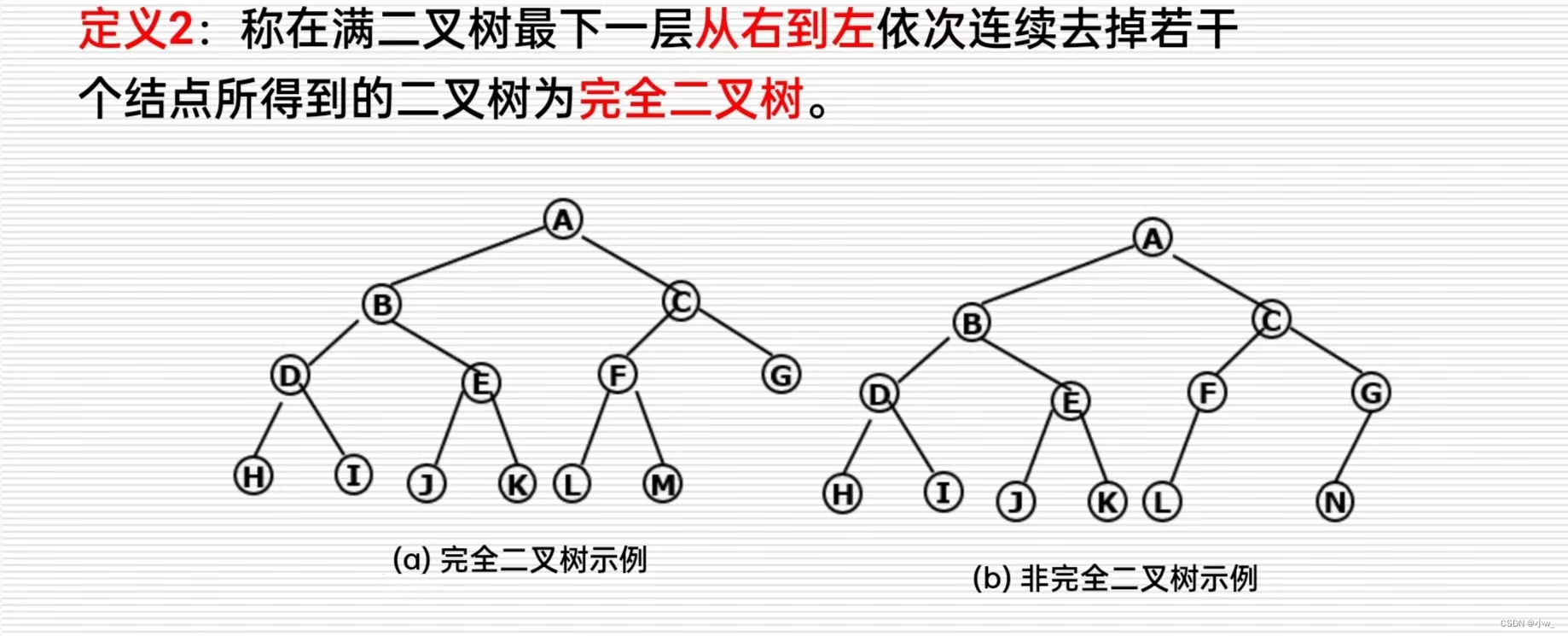
 我们把每一层的层级用 L-x 写在右边如图 。树中节点的最大深度就是树的高度。

由于二叉树每个节点最多有两个孩子，所以，每一层最多有(2的层级次方)个节点

完美二叉树(也叫满二叉树)：

                   每一层都被填满。

右边的式子是在计算这个树所能具有的最多的节点数量(也就是相应完美二叉树的节点数量)即一棵高度为h的二叉树的最大节点数量，利用的是等比数列求和公式求得结果为(2的层级数量的次方-1=2的高度+1次方-1)。从0层到3层一共层级数量是4(感觉层级从1开始好像更直接，不过道理都是一样的)

我们可以直接认为求完美二叉树的高度是约等于logn(以二为底)

对于n个节点来说，最小的高度就是logn。最大高度是n-1。如下图

我们对树的插入、删除、搜索节点等等操作所需时间正比于树的高度。 所以通常，我们想尽可能保持二叉树的高度最小或者平衡。

平衡二叉树：

                      对于每个节点来说，其左右子树的高度差不大于k(k通常为1)。

回顾一下：一个节点的高度就是从该节点到一个叶子节点的最长路径。叶子节点的高度为0.

空树：没有节点，高度为-1。只有一个根节点的树的高度为0。

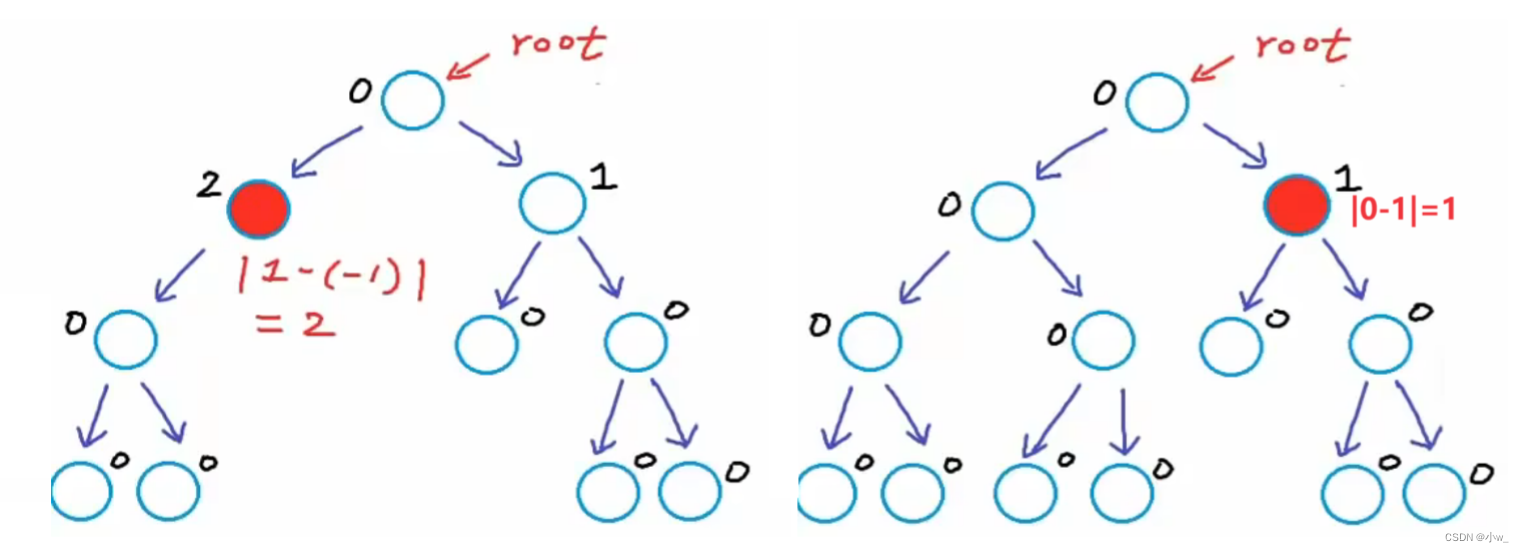
这里k值的计算=左右两子树的高度差的绝对值。严格按照我们所规定的高度进行计算不会出错的(我刚开始算错了几下hh)，可以理解哈。

二叉树的保存方式

动态创建节点

也就是类似链表那种呈现方式，创建一个节点结构体。上面也提到过。

数组实现完全二叉树

用数组特定的能够实现完全二叉树的存储。

如图。我们从根节点开始，由0开始从上至下，从左到右对每个节点进行标号，按标号作为下标存放进数组。

以i作为下标索引，我们发现，对于索引位置为i的节点来说，索引为2i+1所表示的位置为其左孩，2i+2表示的是其右孩。注意该方式只针对完全二叉树。

---

好啦，这次先简单认识一下树。直观的感受到和前面线性的差别，更难了qaq要坚持呀

本人还是小白，仅靠网课资源学习记录笔记，如果有哪里出现错误的说法欢迎指出，非常感谢。

也欢迎交流建议奥。