稀疏编码: LASSO，近端梯度优化（PGD），迭代软阈值算法（ISTA），L-Lipschitz条件，软阈值

在用到稀疏编码时，难免会提到以下概念：

（1）LASSO(Least Absolute Shrinkage and Selection Operatior): 最小绝对收缩选择算子。这个名词听名字比较唬人，很高大上的样子，其实本质很简单，就是给一个解向量增加一个L1范数约束，使解向量的元素尽可能稀疏（0元素越多越好）。L1范数就是一个向量的各元素的绝对值之和。

（2）近端梯度下降（Proximal Gradient Descent, PGD），也可以称为近端梯度优化:听着也很高大上。其实质就是，当一个损失函数比较复杂时，我们把这个损失函数的某个点处用泰勒公式展开为二次函数，用于拟合这个损失函数的局部区域的形状。这样，我们就可以在这个点的附近区域，通过求泰勒公式展开的二次函数的最优解来求损失函数在这个点的近邻区域的局部最优解。PGD可行的一个前提是损失函数在局部满足L-Lipschitz条件，L-Lipschitz条件将在下面被介绍。

所以，“近端”表示的是局部区域，在损失函数曲线上的一个泰勒展开点的近端/附近。

           “近端梯度优化”：在损失函数曲线上的一个点的附近进行泰勒展开，通过执行梯度优化寻找局部最优解。

一个典型的图像如下所示：

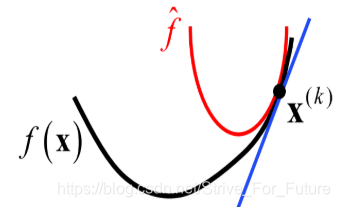
由以上可见，近端梯度优化得到的是一个局部区域的最优解，不是全局最