快速幂及矩阵快速幂——加快运算

为什么需要快速幂呢？

在求解n^k的时候如果k比较小，那么我们可以用k个n相乘来求得结果，但是当k比较大的时候，这种朴素求法就

很容易超时，这时候我们可以使用快速幂算法求解。

在现实生活中，如果让你求2^20次方，你会怎么求？

一般我们会这样来求

1. 让 2 * 2 = 4,这样就能算出2^2的值了。
2. 让 4 * 4 =16,这样就能算出2^4的值了。
3. 让16 * 16 = 256,这样就能算出2 ^ 8的值了。
4. 让256 * 256 = 65536，这样就能算出2 ^ 16的值了。
5. 让65536 * (2 ^ 4) = 1048576,这样就能算出2 ^ 20的值了。

举个例子
11的二进制是1011，11 = 2³×1 + 2²×0 + 2¹×1 + 2º×1，因此，我们将a¹¹转化为算 a2^0 * a2^1 * a2^3，也就是a * 1 * a * 2 * a * 8

快速幂模板

        int quickpow(int a, int b) //求a的b次方
        {
            int ans = 1, base = a;//base初始为a的一次方
            while (b != 0)
            {
                if (b&1 )//若二进制末位为1，取二进制末位
                {
                    ans *= base;//结果乘以a在此位置的次方
                }
                base *= base;//base平方一下，进到下一个二进制位
                b >>= 1;//b的二进制右移动，相当于
            }
            return ans;
        }

还有快速乘

long long cheng(int a,long long n)
        {
            long long res = 0;
            while(n)//与快速幂基本一样，唯一的区别就是把*改成+
            {
                if(n&1)
                {
                    res += a;
                }
                a *= a;
                n>>=1;
            }
            return res;
        }

快速幂取模
编程竞赛有相当一部分题目的结果过于庞大，整数类型无法存储，往往只要求输出取模的结果。
例如(a+b)%p,若a+b的结果我们存储不了，再去取模，结果显然不对，我们为了防止溢出，可以先分别对a取模,b取模，再求和，输出的结果相同。
a mod b表示a除以b的余数。有下面的公式：
(a + b) % p = (a%p + b%p) %p
(a - b) % p = ((a%p - b%p) + p) %p
(a * b) % p = (a%p)*(b%p) %p

int power(long long a, int n)
{
    long long ans = 1;
    while(n > 0) 
    {
        if(n&1) 
        {
            ans *= a;
            ans %= mod;
        }
        a *= a%mod;
        a %= mod;
        n /= 2;
    }
    return ans%mod;
}

矩阵快速幂

矩阵快速幂跟上面的快速幂原理一样，只不过上面是求数的幂而矩阵快速幂是求矩阵的幂。
这里涉及到矩阵的乘法

struct mat
{
    int n,m;//矩阵的行数和列数
    int mp[5][5];//4 X 4 矩阵 
}a,b;
mat matmul(mat a,mat b)//矩阵乘法
{
    int i,j,k;
    mat c;//两个矩阵乘积结果
    for(i=1;i<=a.n;i++)
    {
        for(j=1;j<=b.n;j++)
        {
            for(k=1;k<=a.m;k++)
            {
                c.mp[i][j]+=a.mp[i][k]*b.mp[k][j];
            }
        }
    }
    return c;
}
mat quickpower(mat a,int n)
{
    int i;
    mat ans;
    memset(ans.mp,0,sizeof(ans.mp));
    for(i=1;i<=4;i++)//构造单位矩阵
    {
        ans.mp[i][i]=1;
    }
    while(n)
    {
        if(n&1)
        {
           ans=matmul(ans,a);
        }
        a=matmul(a,a);
        n>>=1;
    }
    return ans;
}

下面看一道例题

求斐波那契数列的第n项，因为n很大所以将结果对1e9+7取余
即f[0]=1,f[1]=1,f[i] = f[i-1]+fi-2

经过推演我们可以发现

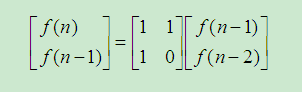
进一步递推我们可以发现

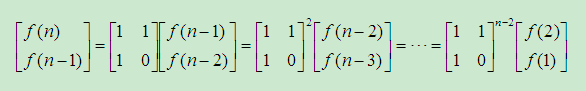
所以我们只要求出图上我们构造的这个矩阵的n-2次幂就行了

#include<iostream>
#include<string.h>
#include<cstdio>
#define MOD 1000000007
using namespace std;
struct mat
{
    int n,m;
    long long mp[3][3];
};
mat matmul(mat a,mat b)
{
    mat c;
    memset(c.mp,0,sizeof(c.mp));
    int i,j,k;
    for(i=1;i<=2;i++)
    {
        for(j=1;j<=2;j++)
        {
            for(k=1;k<=2;k++)
            {
                c.mp[i][j]=(c.mp[i][j]+(a.mp[i][k]*b.mp[k][j])%MOD)%MOD;
            }
        }
    }
    return c;
}
mat quickpower(int n,mat a)
{
    mat ans;
    memset(ans.mp,0,sizeof(ans.mp));
    for(int i=1;i<=2;i++)
    {
        ans.mp[i][i]=1;
    }
    while(n)
    {
        if(n&1)
        {
            ans=matmul(ans,a);
        }
        a=matmul(a,a);
        n>>=1;
    }
    return ans;
}
int main ()
{
    int n;
    while(cin>>n)
    {mat f,a;
    f.mp[1][1]=f.mp[2][1]=1;
    f.mp[1][2]=f.mp[2][2]=0;
    a.mp[1][1]=a.mp[2][1]=a.mp[1][2]=1;
    a.mp[2][2]=0;
    mat b=quickpower(n-2,a);
    f=matmul(b,f);
    cout<<f.mp[1][1]<<endl;
    }
    return 0;
}

还有一个变式例题

定义一个数组，f[i] = f[i-1] + 2*f[i-2] + i^4.

给你f[1] 和 f[2] 求 f[n]。
要使用矩阵快速幂，首先我们必须把递推矩阵推出来
下面是我推的矩阵

初始矩阵是
f[2]
f[1]
16
8
4
2
1

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod = 2147493647;
struct mat
{
    ll jz[7][7];
};
mat init()//返回的是单位矩阵
{
    mat a;
    memset(a.jz,0,sizeof(a.jz));
    for(int i = 0; i < 7; i++)
    {
        a.jz[i][i] = 1;
    }
    return a;
}
mat matmul(mat a,mat b)//矩阵相乘
{
    mat c;
    memset(c.jz,0,sizeof(c.jz));
    for(int k = 0; k < 7; k++)
    for(int i = 0; i < 7; i++)
    if(a.jz[i][k])//在这里有一个小优化，但是感觉一般题目不会卡这里
    for(int j = 0; j < 7; j++)
        c.jz[i][j] = (c.jz[i][j]+(a.jz[i][k]*b.jz[k][j]%mod))%mod;
    return c;
}
mat matpow(ll n)//矩阵快速幂
{
    mat tep;
    tep = {
        1,2,1,4,6,4,1,
        1,0,0,0,0,0,0,
        0,0,1,4,6,4,1,
        0,0,0,1,3,3,1,
        0,0,0,0,1,2,1,
        0,0,0,0,0,1,1,
        0,0,0,0,0,0,1,
    };//原来这样也可以初始化矩阵，学到了，这样更好看一些
    mat ans;
    ans = init();//把ans初始化为单位矩阵
    while(n)
    {
        if(n&1) ans = matmul(ans,tep);
        tep = matmul(tep,tep);
        n >>= 1;
    }
    return ans;
}
int main()
{
    int t;
    ll x,y,n;
    cin >> t;
    while(t--)
    {
        cin >> n >> x >> y;
        mat fir;
        fir.jz[0][0] = y;
        fir.jz[1][0] = x;
        fir.jz[2][0] = 16;
        fir.jz[3][0] = 8;
        fir.jz[4][0] = 4;
        fir.jz[5][0] = 2;
        fir.jz[6][0] = 1;
        mat temp = matpow(n-2);
        fir = matmul(temp,fir);
        cout << fir.jz[0][0] << endl;
    }
    return 0;
}