尺取法及例题

尺取法及例题

尺取法：顾名思义，像尺子一样取一段，借用挑战书上面的话说，尺取法通常是对数组保存一对下标，即所选取的区间的左右端点，然后根据实际情况不断地推进区间左右端点以得出答案。之所以需要掌握这个技巧，是因为尺取法比直接暴力枚举区间效率高很多，尤其是数据量大的时候，所以尺取法是一种高效的枚举区间的方法，一般用于求取有一定限制的区间个数或最短的区间等等。当然任何技巧都存在其不足的地方，有些情况下尺取法不可行，无法得出正确答案。

============================================================================

使用尺取法应该注意下列几点
1、 什么情况下能使用尺取法? 2、何时推进区间的端点？ 3、如何推进区间的端点？ 4、何时结束区间的枚举？

尺取法通常适用于选取区间有一定规律，或者说所选取的区间有一定的变化趋势的情况，通俗地说，在对所选取区间进行判断之后，我们可以明确如何进一步有方向地推进区间端点以求解满足条件的区间，如果已经判断了目前所选取的区间，但却无法确定所要求解的区间如何进一步得到根据其端点得到，那么尺取法便是不可行的。首先，明确题目所需要求解的量之后，区间左右端点一般从最整个数组的起点开始，之后判断区间是否符合条件在根据实际情况变化区间的端点求解答案。

下面我们来看一个例子

![在这里插入图片描述](https://img-blog.csdnimg.cn/20190408213214880.png?x-oss-process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L1N0aWxsYm9yaW5n,size_16,color_FFFFFF,t_70`

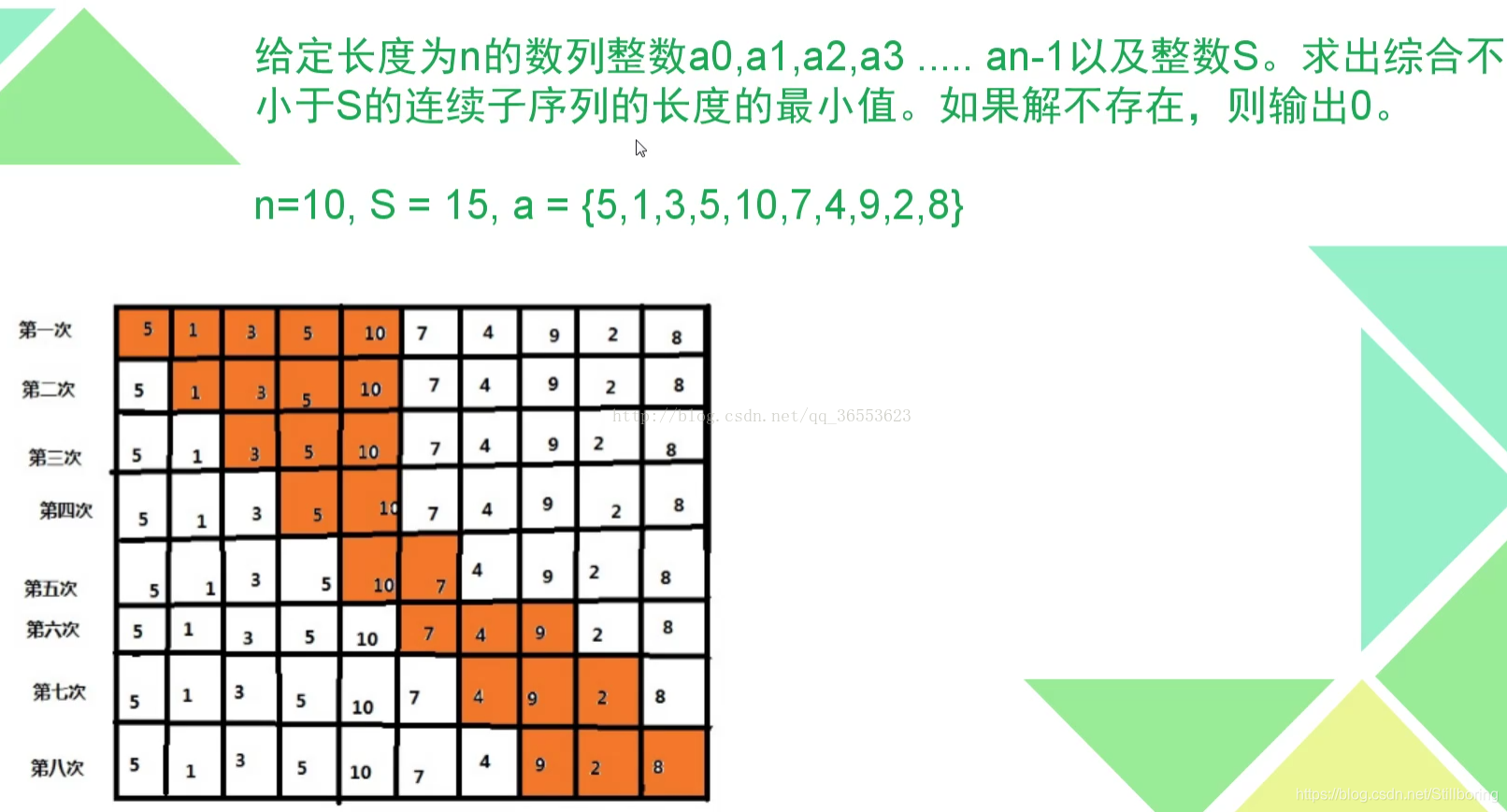
下面是伪代码实现：

int l,r,sum,i,s;
i=sum=l=0;
result=n+1;
while(1)
{
    while(i<n&&sum<s)//从左端点开始
    {
        sum+=a[i];
        i++;
    }
    if(sum<s)//条件不满足了，就退出循环
    {
        break;
    }
    MIN=i-l;
    result=min(MIN,result);
    sum-=a[l++];//尺取法左端点前进
    
}

1、 Poj3061题意：给定一个序列，找出最短的子序列长度，使得其和大于或等于S。

分析：首先，序列都是正数，如果一个区间其和大于等于S了，那么不需要在向后推进右端点了，因为其和也肯定大于等于S但长度更长，所以，当区间和小于S时右端点向右移动，和大于等于S时，左端点向右移动以进一步找到最短的区间，如果右端点移动到区间末尾其和还不大于等于S，结束区间的枚举。

#include <cstdio>
#include <algorithm>
#include <cstring>
#define MAX 100005
#define LL long long
#define INF 0x3f3f3f3f
using namespace std;
LL a[100010];
int n, t, ans = INF;
LL sum, s;
int main()
{
    scanf("%d", &t);
    while (t--){
        scanf("%d %I64d", &n, &s);
        for (int i = 0; i < n; i++) scanf("%I64d", a+i);
        int st = 0, en = 0;
        ans = INF; sum = 0;
        while (1){
            while (en<n && sum<s) sum += a[en++];
            if (sum < s) break;
            ans = min(ans, en-st);
            sum -= a[st++];
        }
        if (ans == INF) ans = 0;
        printf("%d\n", ans);
    }
    return 0;
}

2、 poj3320题意：一本书有P页，每一页都一个知识点，求去最少的连续页数覆盖所有的知识点。

分析：和上面的题一样的思路，如果一个区间的子区间满足条件，那么在区间推进到该处时，右端点会固定，左端点会向右移动到其子区间，且其子区间会是更短的，只是需要存储所选取的区间的知识点的数量，那么使用map进行映射以快速判断是否所选取的页数是否覆盖了所有的知识点。

#include<iostream>
#include<algorithm>
#include<cstdio>
#include<map>
#include<set>
#include<string>
#define MAX 100010
#define INF 0x3f3f3f3f
using namespace std;
int a[MAX];
map<int,int>cnt;
set<int>t;
int p,ans=INF,l,r,sum;
int main ()
{
    int i;
    scanf("%d",&p);
    for(i=0;i<p;i++)
    {
        scanf("%d",&a[i]);
        t.insert(a[i]);
    }
    int num=t.size();
    while(1)
    {
        while(l<p&&sum<num)
        if(cnt[a[r++]]++==0)//如果这个知识点没有选过，就选取它并标记。
            sum++;
            if(sum<num)
                break;
        ans=min(ans,r-l);
        if(--cnt[a[l++]]==0)
            sum--;
            /*如果左端点这个知识点已经选过了，那么就把它踢出去，知识点的个数要减一，之后再继续循环,如果没有选择过那么就使左端点向右，已选知识点数量不变*/
    }
    printf("%d\n",ans);
    return 0;
}