洛谷 P1182 数列分段 Section II

最新推荐文章于 2023-11-20 00:00:00 发布

原创最新推荐文章于 2023-11-20 00:00:00 发布 · 483 阅读

2 ·

CC 4.0 BY-SA版权

刷题专栏收录该内容

39 篇文章

订阅专栏

博客围绕将长度为N的正整数数列分成M段，求每段和的最大值最小的问题展开。介绍了输入输出格式、样例，指出普通枚举会超时，需用二分思想枚举答案，即二分答案，通过枚举每段数列和的最大值来验证分段情况。

对于给定的一个长度为N的正整数数列 A_{1\sim N}A1∼N，现要将其分成 MM（M\leq NM≤N）段，并要求每段连续，且每段和的最大值最小。

关于最大值最小：

例如一数列 4\ 2\ 4\ 5\ 14 2 4 5 1 要分成 33 段。

将其如下分段：

[4\ 2][4\ 5][1][4 2][4 5][1]

第一段和为 66，第 22 段和为 99，第 33 段和为 11，和最大值为 99。

将其如下分段：

[4][2\ 4][5\ 1][4][2 4][5 1]

第一段和为 44，第 22 段和为 66，第 33 段和为 66，和最大值为 66。

并且无论如何分段，最大值不会小于 66。

所以可以得到要将数列 4\ 2\ 4\ 5\ 14 2 4 5 1 要分成 33 段，每段和的最大值最小为 66。

输入格式

第 1 行包含两个正整数 N,M。

第 2行包含 N个空格隔开的非负整数Ai，含义如题目所述。

输出格式

一个正整数，即每段和最大值最小为多少。

输入输出样例

输入 #1

5 3
4 2 4 5 1

输出 #1

说明/提示

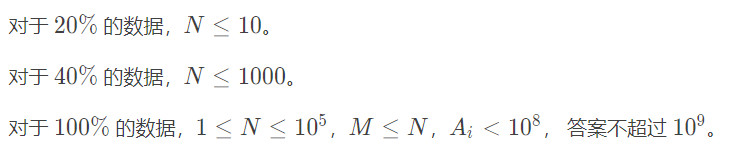
分析：数据量在1e5,普通枚举时间复杂度在1e10，显然会超时。

需要使用二分的思想来枚举，也就是二分答案。

枚举每段数列和的最大值Max，然后来利用枚举出来的最大值来验证是否能在保证每段数列的和<=Max的条件下，分成num段(num<=m)。

#include<bits/stdc++.h>
using namespace std;
int n,m;
const int maxn  = 1e5+10;
long long a[maxn];
bool check(long long mid)
{
    int num = 1;
    long long sum = 0;
    for(int i =1;i<=n;i++)
    {
        if(sum+a[i]<=mid)
        {
            sum+=a[i];
        }
        else
        {
            sum=a[i];
            num++;
        }
    }
    if(num>m)
        return false;
    else
        return true;
}
int main()
{
    cin>>n>>m;
    long long l = 0,r=0;
    for(int i =1;i<=n;i++)
    {
        scanf("%d",&a[i]);
        l=max(l,a[i]);
        r +=a[i];
    }
    while(l<=r)
    {
        long long mid = (l+r)>>1;
        if(check(mid))
        {

            r=mid-1;
        }
        else
        {
            l=mid+1;
        }
    }
    cout<<r+1<<endl;
    return 0;
}