MATLAB代码：基于元模型优化的虚拟电厂主从博弈优化调度模型关键词：元模型虚拟电厂主从博弈优化

MATLAB代码解析：虚拟电厂主从博弈优化调度模型——基于元模型与优化算法的探索

一、背景介绍

随着能源转型和绿色发展的趋势，虚拟电厂作为一种新型电力架构，在能源管理和优化调度中扮演着越来越重要的角色。在此背景下，主从博弈优化调度模型的应用显得尤为重要。本文将围绕MATLAB代码，深入探讨基于元模型优化的虚拟电厂主从博弈优化调度模型的相关内容。

二、代码概述

本篇博客将详细解析基于MATLAB平台的虚拟电厂主从博弈优化调度模型的代码实现。该模型主要涉及元模型优化算法的应用，以及双层结构的优化调度策略。代码主要分为以下几个步骤：

数据准备：包括虚拟电厂的数据收集、模型参数设定等准备工作。
元模型构建：构建基于元模型的优化调度策略，以最小化运行成本为目标。
双层优化调度模型构建：上层为虚拟电厂联合调度模型，以最小化运行成本为目标；下层采用粒子群算法求解市场运营商的电价优化。

三、代码分析

元模型构建与应用

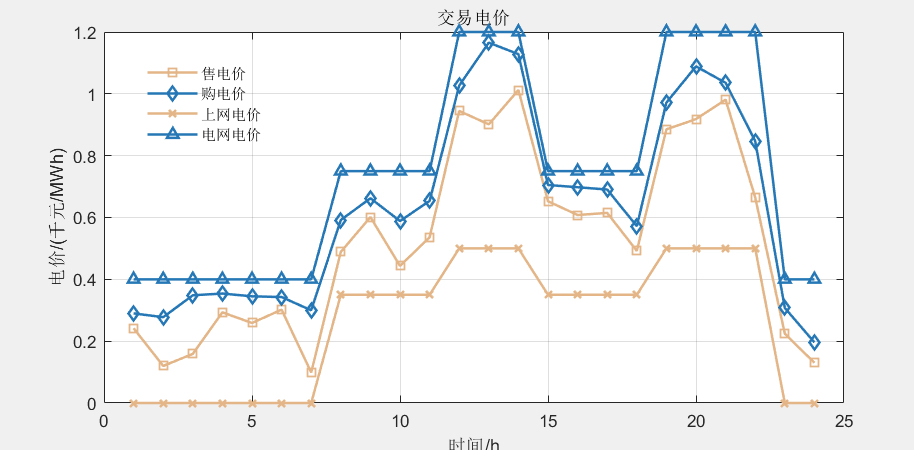
在元模型构建过程中，首先通过分析虚拟电厂的运行特性、市场环境等因素，确定了优化目标。然后，构建了多虚拟电厂的联合调度模型，实现了不同虚拟电厂之间的协同运行和资源的最优配置。此外，还考虑了市场运营商的电价优化问题，通过优化售电电价和购电电价，实现了整体电价的最优决策。

粒子群算法的应用

在双层优化调度模型中，上层采用了粒子群算法作为求解器。粒子群算法是一种模拟自然界生物进化过程的优化算法，可以有效解决大规模、非线性、约束性优化问题。通过粒子群算法求解市场运营商的电价优化问题，可以实现多虚拟电厂在竞争和合作下电价的最优决策。

四、案例应用

该代码通过模拟真实情况或复现已有的元模型优化算法应用于多虚拟电厂动态定价和能量管理领域。该模型的构建和求解过程可为其他虚拟电厂的实际运行提供借鉴和参考。此外，通过CPLEX等仿真平台，可以进行仿真验证和效果评估。

五、总结与展望

本代码展示了基于元模型优化的虚拟电厂主从博弈优化调度模型的实现和应用。该模型在实际应用中具有重要价值，可以为虚拟电厂的运行和管理提供有力的支持。未来，随着技术的不断发展和进步，该模型有望在更多领域得到应用和推广。
MATLAB代码：基于元模型优化的虚拟电厂主从博弈优化调度模型
关键词：元模型虚拟电厂主从博弈优化调度
参考文档：《基于元模型优化算法的主从博弈多虚拟电厂动态定价和能量管理》复现元模型
仿真平台：MATLAB+CPLEX平台
主要内容：代码主要做的是虚拟电厂的优化调度策略，其实是多虚拟电厂/微网的优化调度策略，模型为双层，首先下层模型中，构建了多个虚拟电厂的联合调度模型，以每个虚拟电厂的运行成本最低为优化目标，而上层为领导者模型，主要是优化市场运营商的电价，包括售电电价和购电电价的优化，从而构成了主从博弈模型，在求解的过程中，上层采用的是粒子群算法，而下层则是调用CPLEX求解器进行求解，由于模型整体规模较大，故采用了元模型算法加速求解！
代码为精品代码，与目前流传的版本不一致，从实现效果和注释清晰度上就可以看出区别，请不要混为一谈！
这段程序主要是一个电力市场中的动态定价博弈模型。它涉及到超拉丁采样（LHS）生成初始样本点、调用下层博弈模型计算每个虚拟电力厂（VPP）的交易电量、修正Kriging模型计算每组样本点对应的目标函数值、关键区域划分并计算各个区域的最优值、在每个关键区域上采用粒子群算法求解局部最优电价等步骤。

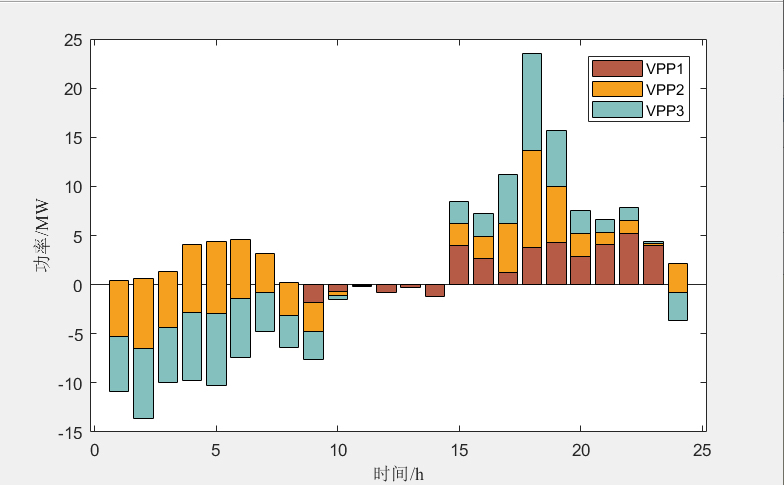
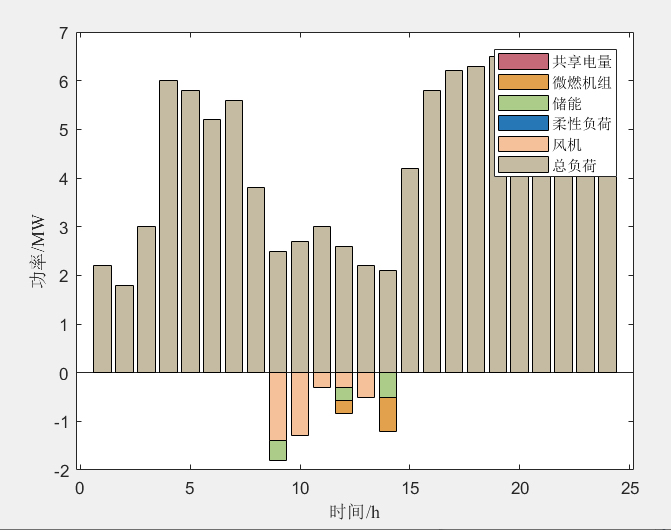
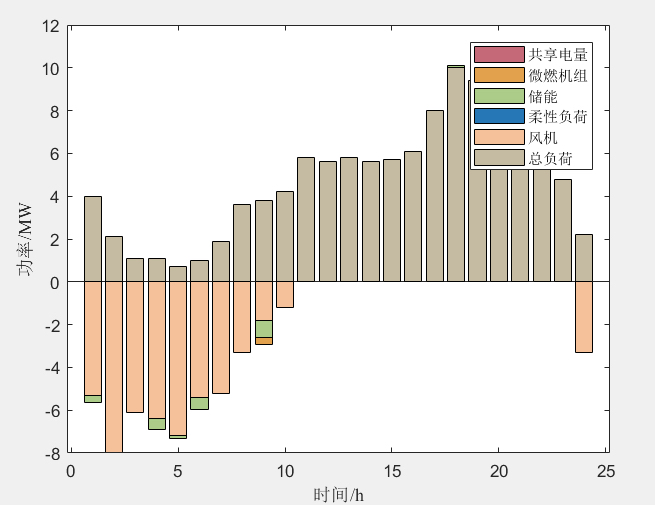
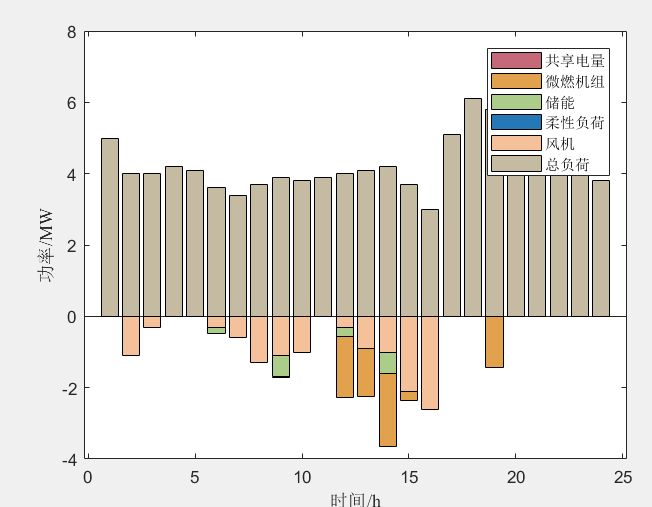
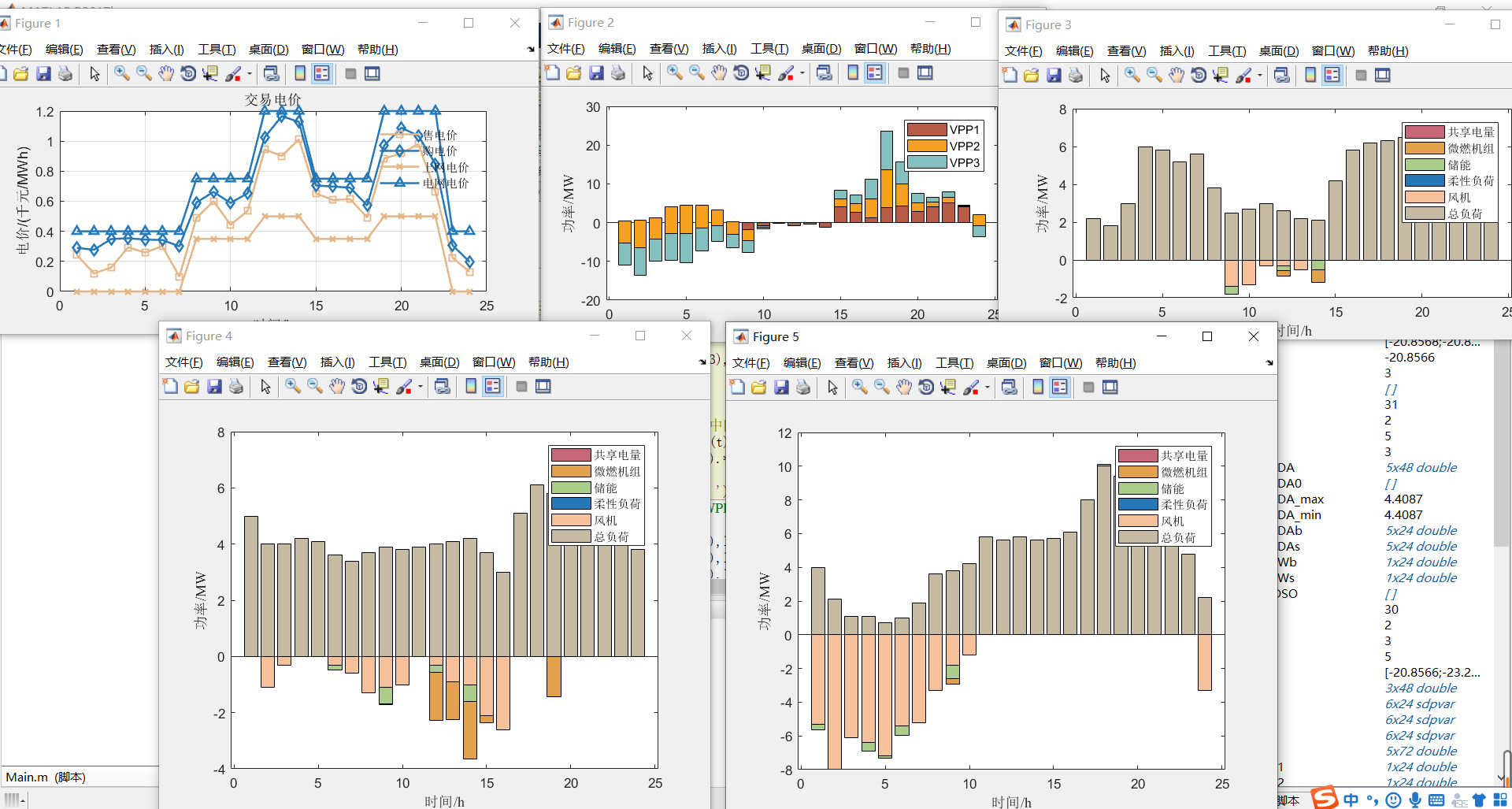
首先，程序通过超拉丁采样（LHS）生成了一些初始样本点，用于后续的计算。然后，通过生成的样本点调用下层博弈模型，计算出每个VPP的交易电量，构成样本数据集。接下来，程序修正Kriging模型，计算每组样本点对应的目标函数值。然后，程序进行关键区域划分，并计算各个区域的最优值。在每个关键区域上，采用粒子群算法求解局部最优电价。最后，程序输出结果，包括DSO的收益和一些图表展示。

程序中涉及到的知识点包括超拉丁采样（LHS）、Kriging模型、粒子群算法等。超拉丁采样是一种用于生成均匀分布的采样点的方法，Kriging模型是一种用于拟合数据的插值模型，粒子群算法是一种用于优化问题的启发式算法。