Diff-Unmix：将扩散模型从高光谱图像转移到丰度空间

原创已于 2025-12-29 18:25:49 修改 · 602 阅读

CC 4.0 BY-SA版权

文章标签：

于 2025-12-29 18:20:22 首次发布

论文：Unmixing Diffusion for Self-Supervised Hyperspectral Image Denoising

来源：Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), 2024, pp. 27820-27830

作者：Haijin Zeng, Jiezhang Cao, Kai Zhang, Yongyong Chen, Hiep Luong, Wilfried Philips;

一、引言

近年来，扩散模型（Diffusion Model）在图像生成与复原任务中展现出强大的建模能力，并逐渐被引入到高光谱图像（HSI）去噪问题中。已有一些方法并未将扩散模型直接作用于原始高光谱图像，而是结合低秩或子空间模型，先将 HSI 映射到低维表示，再在该空间中进行扩散建模，以降低建模维度和计算复杂度。

然而，这类低维表示的核心目标在于数值压缩与稳定性，而非刻画高光谱图像中材料组成与空间结构的物理语义。当扩散模型作用于缺乏语义约束的子空间表示时，其生成结果在复杂噪声或跨场景条件下的稳定性与一致性仍然值得进一步探讨。

在高光谱成像领域，谱解混模型为这一问题提供了另一种视角。通过将高光谱图像表示为光谱端元及其对应的丰度图，谱解混在实现降维的同时，引入了具有明确物理含义的中间表示。其中，丰度图描述了不同材料在空间上的分布结构，使其成为一个结构受限、语义更明确的建模空间。

基于这一观察，Diff-Unmix 将扩散模型引入丰度空间，而非直接作用于原始 HSI 或低秩子空间。这一设计体现了一种建模层级上的转变：从侧重数值低维性的子空间表示，转向具有物理语义约束的中间表示。

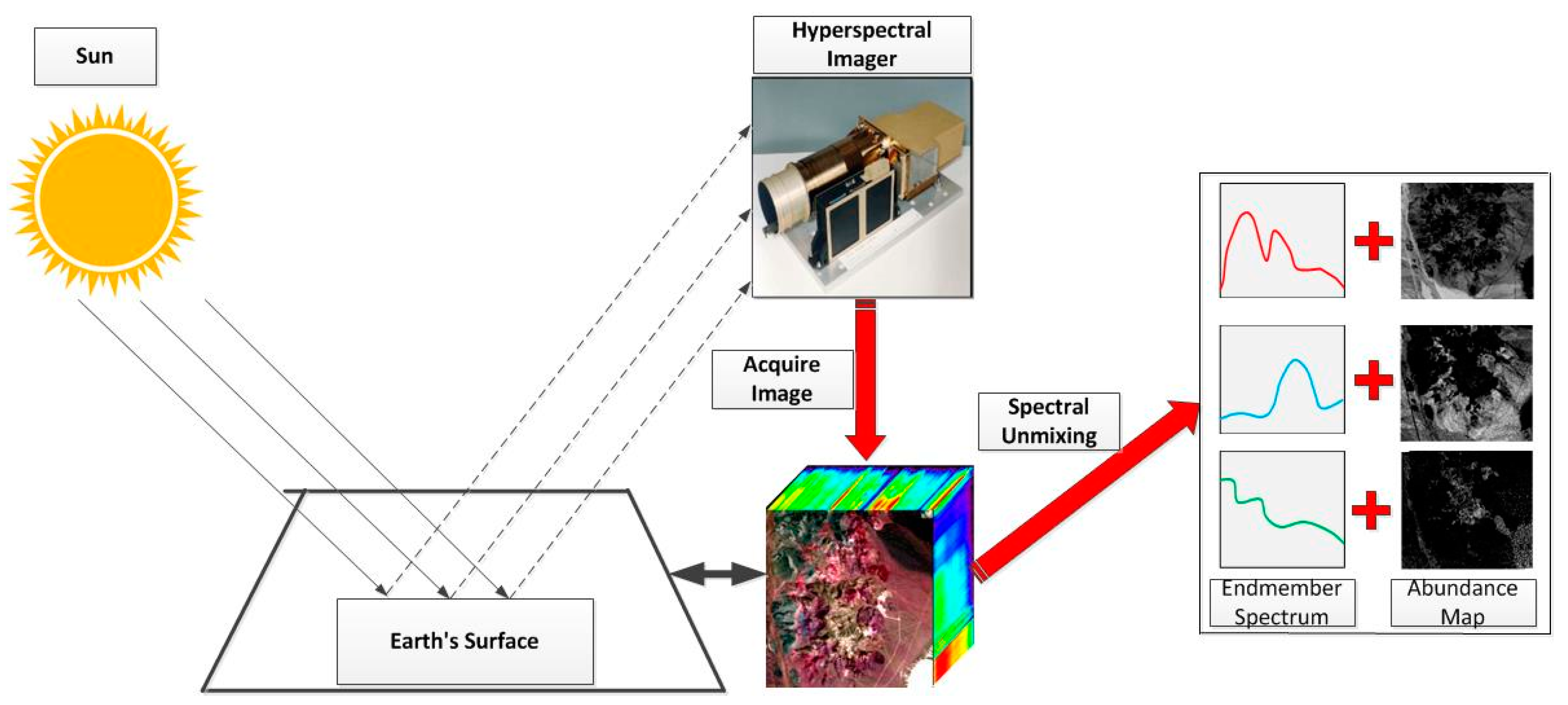
从整体流程上看，Diff-Unmix 并不是对已有扩散式高光谱去噪方法的简单延伸，而是体现了一种建模层级上的转变：
即从“直接对高光谱图像进行扩散建模”，转向“在具有物理意义的中间表示中引入生成模型”。

本文将围绕这一思路，对 Diff-Unmix 的整体框架进行梳理，并重点分析这种建模转变所带来的优势与启示。

二、从低秩子空间到谱解混：Diff-Unmix 的整体思路

在已有的扩散式高光谱去噪方法中，一个常见的做法是：先通过低秩分解或子空间投影降低数据维度，再在该低维表示上引入扩散模型进行建模。这类方法（如 HIR-DIFF）在工程上是合理的：
降维可以显著缓解高光谱数据带来的计算与建模压力，同时也为扩散模型提供一个数值上更稳定的输入空间。然而，这种“低维表示”本质上仍然是以数值低秩性为核心的统计子空间。其目标主要在于压缩冗余信息，而并不关心这些维度在物理或语义层面上代表什么。

Diff-Unmix 的核心思想，正是对这一建模选择的重新审视。

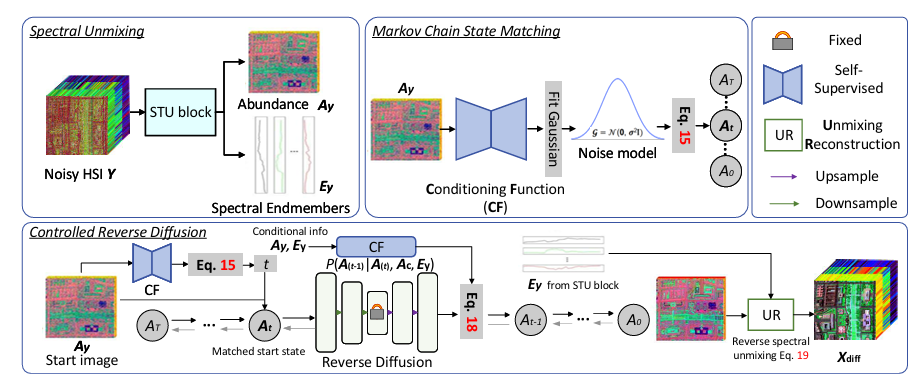
从整体框架上看，Diff-Unmix 的整体流程可以被概括为三步：

将噪声高光谱图像分解为谱解混形式
只在丰度表示上进行扩散建模
利用端元将去噪后的丰度重建回高光谱图像

从“输入–输出”的角度看，这仍然是一个高光谱图像去噪方法；
但从“建模层级”的角度看，它已经将去噪问题拆解成了两个不同层次的问题。

第一层：结构与物理约束如何保证？
由谱解混模型负责。

第二层：细节与分布如何恢复？
由扩散模型负责。

正是这种分工，使得 Diff-Unmix 的整体逻辑更容易被拆解和理解。

2.1 从“数值子空间”到“结构表示”

与低秩分解不同，谱解混并不只是追求降维，而是引入了一种具有明确结构假设的表示形式。
在谱解混模型中，高光谱图像被表示为少量光谱端元及其对应的丰度图的组合，其中：

端元描述材料的光谱特性，假设在噪声变化下相对稳定；
丰度图描述不同材料在空间上的分布比例，承载了主要的空间结构信息。

这一表示方式并非简单的数值压缩，而是显式引入了“材料 × 空间分布”的建模假设。

从这一角度看，Diff-Unmix 所做的并不是“换一个更复杂的网络”，而是将扩散模型的作用对象，从一个抽象的数值子空间，转移到一个具有结构语义的中间表示之中。

2.2 将去噪问题拆解为两个层次

基于谱解混表示，Diff-Unmix 将高光谱去噪问题拆解为两个相对独立的子问题：

结构建模问题：
通过谱解混网络，从噪声观测中提取一个在不同噪声条件下尽量稳定的结构表示（丰度图）。
分布建模问题：
在该结构表示空间中，引入扩散模型，对丰度分布进行生成式修复与细节补偿。

这一拆解具有重要含义：扩散模型不再需要直接面对高光谱数据的高维性和强谱相关性，
而是被限制在一个低维、结构明确、形式统一的表示空间中运行。

2.3 为什么扩散只作用在丰度空间

在 Diff-Unmix 中，扩散模型仅作用于丰度图，而不直接作用于原始高光谱图像或端元表示。主要考虑到：

丰度图在空间结构上更接近自然图像，适合利用现有的二维扩散模型；
噪声对高光谱图像的影响，往往在丰度表示中更加集中；
光谱一致性由端元表示显式约束，避免扩散模型在光谱维度上“自由生成”。

因此，在这一框架下，扩散模型的角色不再是“去噪器”，而是一个在物理模型约束下进行细节修复的生成模块。

三、为扩散而设计的谱解混表示：STU 的角色定位

在 Diff-Unmix 中，谱解混并不是作为一个独立目标存在的模块，而是承担了一个更具工具性的角色：为扩散模型构造一个稳定、低维、结构受限的中间表示空间。这一定位决定了 STU 的设计目标并非“最优解混”，而是“可扩散性”。

3.1 STU 的目标不是“解得准”，而是“解得稳定且一致”

在 Diff-Unmix 框架中，Spectral Transformer Unmixing Network（STU）并未被设计为一个追求谱解混物理精度的独立模块，而是作为扩散建模之前的中间表示构造器存在。这一定位决定了其设计目标与传统谱解混方法存在本质差异。

在经典谱解混任务中，端元光谱的物理可解释性以及丰度估计的准确性通常是评价模型优劣的核心标准。然而，在 Diff-Unmix 所采用的自监督设定下，既缺乏干净高光谱图像作为参考，也不存在可用于验证“真实端元”的外部先验。在这种背景下，STU 的核心目标并非恢复真实材料组成，而是构造一个在不同噪声条件下具有一致性和稳定性的表示空间。

具体而言，STU 更关注以下三个方面：
（1）在不同噪声强度或噪声实现下，同一场景得到的丰度表示应保持较高一致性；
（2）端元估计在空间与光谱维度上应具备稳定性，避免随噪声变化而发生剧烈漂移；
（3）解混结果能够在观测一致性约束下稳定重建输入图像，为后续扩散过程提供可靠条件。

这些目标并不意味着 STU 完全忽略解混结果的合理性，而是表明其不将端元与丰度的物理真实性作为最终优化目标。相较之下，STU 更强调“是否为扩散模型提供了一个可控、低维且结构稳定的建模空间”。从这一角度看，其输出的丰度图更接近一种任务驱动的结构编码，而非严格意义上的物理丰度估计。

3.2 双分支结构：稳定性优先于统一建模

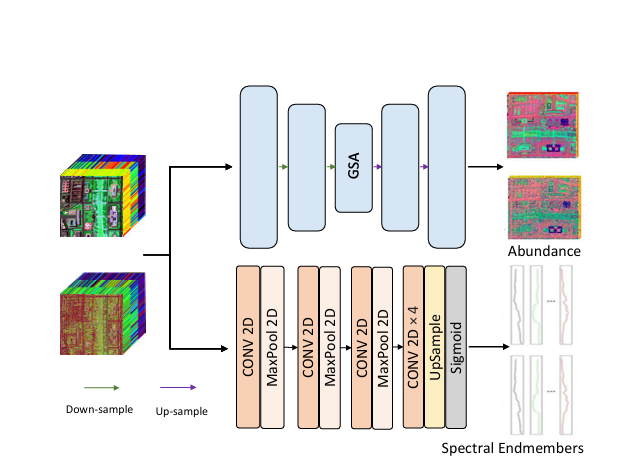
STU 采用双分支结构，分别处理丰度和端元，这一设计并非追求模型复杂度，而是源于对两类变量建模需求差异的明确区分：

丰度图主要承载空间结构信息，且直接作为扩散模型的输入；
端元主要承担光谱约束角色，其稳定性比精细建模更为重要。

因此，丰度分支引入 Transformer 以增强结构表达能力，而端元分支则采用相对保守的卷积建模策略，以减少噪声扰动带来的不稳定性。这一结构体现了一种明确的取舍：将表达能力集中在扩散所依赖的变量上，而非平均分配。

3.3 Global Spectral Attention：一种有意识的建模简化

在丰度分支中，STU 并未采用标准的空间自注意力，而是引入 Global Spectral Attention（GSA），将注意力计算限定在光谱维度。

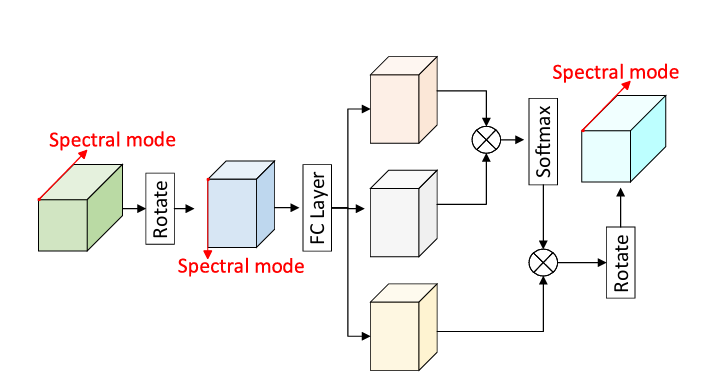
这一设计不仅是出于计算效率的考虑，更隐含了一个关键假设：在谱解混阶段，建模光谱相关性比建模空间长程依赖更为重要。通过这一选择，STU 在解混阶段有意弱化了空间建模能力，而将空间细节的恢复任务交由后续的扩散模型完成。这种“能力分工”使得整个框架在复杂度与表达能力之间取得平衡。

3.4 自监督约束下的解混：稳定性而非真实性

由于缺乏干净高光谱图像作为监督信号，STU 的训练依赖一组一致性约束：解混结果应能够重建回输入观测，同一场景在不同噪声条件下得到的丰度应尽量接近，相应的端元估计应保持稳定。

这些约束确保了解混输出在噪声变化和变换扰动下的稳定性，但并未直接约束其物理意义。因此，STU 的解混结果更应被视为一种任务驱动的中间表示，其价值体现在为扩散模型提供一个可控、稳定的建模空间。

四、丰度扩散的条件约束

在完成谱解混之后，Diff-Unmix将去噪问题的重心进一步转移到丰度空间中，并在该空间内引入扩散模型进行生成式修复。这一部分的关键不在于“是否使用扩散模型”，而在于如何在不破坏物理与观测一致性的前提下，有限度地利用扩散模型的生成能力。

4.1 丰度上的扩散建模形式

Diff-Unmix 采用标准扩散模型的前向加噪过程，对丰度图 A0 定义：

$A_t = \sqrt{\tilde{a}_t} A_0 + \sqrt{1 - \tilde{a}_t} \epsilon, \quad \epsilon \sim \mathcal{N}(0, I)$

其中 $\tilde{a}_t = \prod_{i=1}^t a_i$ ，t 表示扩散时间步。

需要注意的是，在实际应用中 A0是未知的，模型只能获得由谱解混网络预测的噪声丰度 Ay。因此，Diff-Unmix 的扩散过程并非从纯噪声开始，而是围绕如何利用已有的 Ay来启动和约束反向扩散。

4.2 条件模块 Φ：扩散过程中的结构约束机制

为在扩散过程中引入结构约束，论文定义了一个条件映射函数 Φ，其作用是从噪声丰度中生成条件丰度：

$A_C = \Phi(A_y)$

从流程上看，Φ 并不直接参与最终的高光谱重建，而是作为扩散模型的条件输入存在。其输出在反向扩散过程中与当前丰度状态及端元信息共同使用，用于对丰度的更新过程进行约束，从而使生成结果与谱解混阶段得到的结构保持一致。

在反向扩散阶段，扩散模型在预测噪声或更新丰度状态的同时，引入由 Φ 生成的条件丰度，对采样过程进行引导。这种条件引入方式使得扩散模型不再完全依赖自身的生成能力，而是在一定程度上参考了解混结果所提供的结构信息。

论文将 Φ 设计为轻量级条件网络，其网络结构并非方法的核心关注点。相较于具体的实现形式，作者更强调 Φ 在自监督设定下作为条件信息参与扩散建模的使用方式，即通过条件输入的形式，将谱解混结果与丰度扩散过程联系起来。

4.3 State Matching：反向扩散的起始时间步选择

与标准扩散模型从纯噪声状态 t=T开始反向采样不同，Diff-Unmix 引入了 state matching 策略，用于确定更合适的反向扩散起点。

论文中通过估计噪声丰度 Ay中残差噪声的标准差 σ，并将其与扩散过程中的噪声调度参数进行匹配，确定起始时间步：

$t^* = \arg\min_t \left\| \sqrt{\beta_t} - \sigma \right\|_2$

其中 βt为扩散过程中的噪声方差参数。

该策略隐含一个重要假设：噪声丰度可以被单一高斯分布刻画，并与扩散过程中的某一时间步相匹配。这一假设在合成高斯噪声下通常成立，但在复杂真实噪声（如条带噪声、系统噪声）场景中，其适用性存在不确定性。

4.4 受控的反向扩散更新

在确定起始时间步后，反向扩散过程按照标准 DDPM 形式进行，其更新公式为：

$A_{t-1} = \frac{1}{\sqrt{a_t}} \left( A_t - \frac{1 - a_t}{\sqrt{1 - \tilde{a}_t}} \epsilon_\theta(A_t, t) \right) + \sqrt{1 - a_t} z_t, \quad z_t \sim \mathcal{N}(0, I)$

其中 ϵθ(⋅)表示预训练扩散模型的噪声预测网络。在扩散结束后，得到去噪后的丰度估计 A0，最终的高光谱图像通过谱解混模型进行重建：

$\chi_{\text{dir}} = \hat{A}_0 {}_{\times 3} E_y$

五、实验

论文通过合成噪声与真实噪声两类实验，对 Diff-Unmix 的有效性进行了验证。

5.1 合成噪声条件下的定性对比

在合成高斯噪声条件下，Diff-Unmix 在 PSNR、SSIM 等指标上整体表现优于多数对比方法，尤其是在较高噪声水平（如 σ = 0.3）的设置下，其优势更加明显。从视觉结果来看，Diff-Unmix 能够在抑制噪声的同时保留较多细节结构，相比传统低秩方法常见的过平滑现象，其结果更具层次感。

需要指出的是，在这一设置下，State Matching 与噪声建模假设通常是成立的，因此扩散模型的生成能力能够较为充分地发挥作用。这也使得合成噪声实验在一定程度上更有利于 Diff-Unmix 的整体设计。

5.2 真实噪声场景下的视觉结果

在真实噪声场景中，不同方法之间的差异更加明显。相比直接在高光谱图像上进行扩散的方案，Diff-Unmix 在结构保持方面表现更为稳定，较少出现明显的结构漂移或跨波段不一致问题。

这一现象并非单纯来自扩散模型本身，而更多得益于谱解混表示所引入的结构约束：扩散过程被限制在丰度空间内，而光谱一致性由端元表示显式保证。这一分工在复杂噪声条件下有效降低了生成式模型“自由发挥”所带来的风险。

5.3 消融实验

消融实验从定性角度验证了 Diff-Unmix 各组成模块的作用。

STU 的主要价值并不体现在单次解混结果的最优性上，而在于其在不同噪声条件下提供了相对稳定的一致表示；
条件函数 Φ则在扩散过程中起到结构锚定作用，缺失该条件时，生成结果更容易出现局部不稳定；
State Matching 的引入显著降低了推理时间，其效果在加速层面尤为直接。

这些结果共同表明，Diff-Unmix 的性能并非由某一单独模块决定，而是依赖于“结构表示 + 受控生成”这一整体框架。

5.4 失败案例分析

论文中展示的过增强示例表明，即便在多重约束下，扩散模型仍可能引入并非来自观测的伪结构。
这一现象并非实现缺陷，而是生成式模型在去噪任务中不可回避的风险。

从实验角度看，这些失败案例也间接说明：Diff-Unmix 的优势主要体现在结构补偿与细节恢复上，而非严格意义上的保真重建。在对重建真实性要求极高的应用场景中，这一点需要被谨慎对待。

六、总结与方法局限性

本文围绕 Diff-Unmix 在高光谱图像去噪任务中的整体设计思路，对其方法动机、关键模块与实验表现进行了梳理。与传统低秩或子空间方法主要关注数值压缩不同，Diff-Unmix 的核心贡献在于将扩散模型嵌入具有物理语义约束的中间表示之中，而非直接作用于原始高光谱图像本身。

在这一框架下，高光谱去噪被拆解为两个层次的问题：一是通过谱解混构造结构稳定的表示空间，二是在该空间内对丰度分布进行受控的生成式修复。这种“先约束、再生成”的思路，使扩散模型的生成能力受到物理模型与观测一致性的双重限制，从而在一定程度上缓解了生成式方法在高光谱任务中常见的结构漂移风险。

从实现角度看，STU并非追求解混精度的极致，而是服务于后续扩散建模；条件函数与 State Matching 则分别在结构约束与推理效率上发挥作用。Diff-Unmix 的整体性能并非来源于某一单独模块，而是依赖于“结构表示 + 受控生成”这一整体设计逻辑。

与此同时，论文也明确展示了该方法的局限性。由于扩散模型本质上属于生成式模型，在个别场景下仍可能引入过增强的细节，产生并非来自原始观测的伪结构。 即便在多重约束下，这一风险也无法被完全消除。此外，Diff-Unmix 的效果在一定程度上依赖谱解混阶段输出的稳定性，当解混结果受到复杂噪声或场景变化影响时，后续扩散建模的可靠性也可能随之下降。

从适用场景的角度看，Diff-Unmix 更适合用于以视觉分析和结构恢复为目标的高光谱预处理任务，而非对物理真实性要求极高的定量反演场景。 这一定位既解释了其在细节恢复方面的优势，也为其潜在风险划定了清晰边界。

总体而言，Diff-Unmix 的价值并不在于单一性能指标上的显著领先，而在于提出了一条具有代表性的建模路径：将生成模型置于物理模型约束之下使用，而非以生成能力取代物理建模。 这一思路为后续工作在模型约束、生成稳定性以及解混鲁棒性等方向提供了值得进一步探索的空间。