MATLAB画节点的平滑曲线

代码解释：

1. 生成点：
   • n = 100;：指定要生成的点的数量为 100 个。
   • x = 1:n;：生成从 1 到 100 的递增 x 坐标。
   • y = randn(1, n);：使用 randn 函数生成 100 个服从标准正态分布的随机数作为 y 坐标，从而实现 y 坐标的随机波动。
2. 绘制原始点：
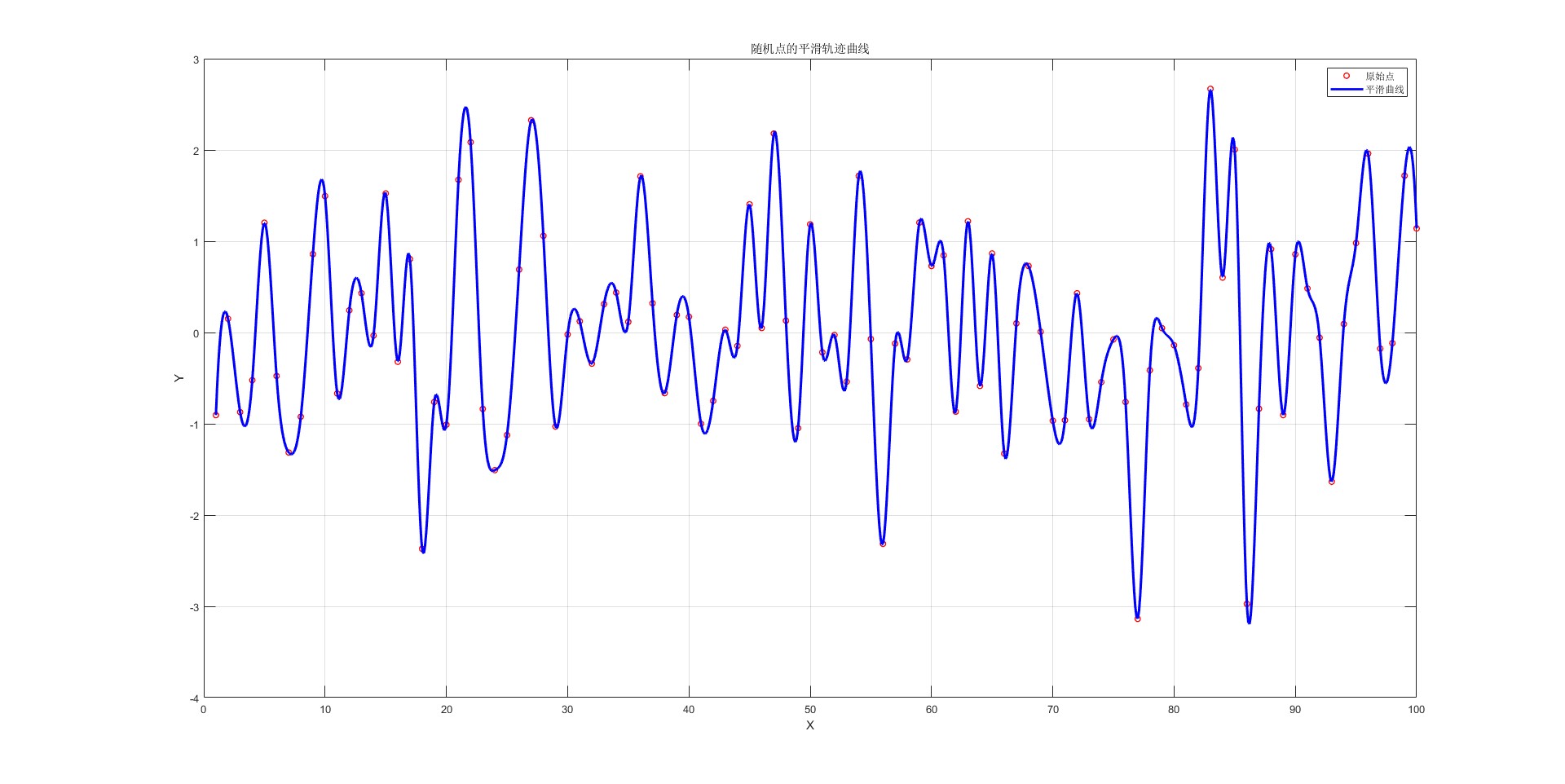
   • plot(x, y, 'ro', 'MarkerSize', 5, 'LineWidth', 1);：将生成的 100 个点以红色圆圈的形式绘制在图形窗口中。
3. 生成平滑曲线：
   • xx = linspace(min(x), max(x), 1000);：在 x 坐标的最小值和最大值之间生成 1000 个均匀分布的点，用于绘制平滑曲线。
   • yy = spline(x, y, xx);：使用 spline 函数对原始的 x 和 y 坐标进行样条插值，得到 xx 对应的 yy 坐标，从而生成平滑曲线。
4. 绘制平滑曲线：
   • plot(xx, yy, 'b-', 'LineWidth', 2);：将生成的平滑曲线以蓝色实线的形式绘制在图形窗口中。
5. 设置图形属性：
   • 添加坐标轴标签、标题、网格和图例，使图形更加清晰和易读。
6. 

% 生成 100 个点
n = 100;
% 生成递增的 x 坐标
x = 1:n;
% 生成 y 坐标，让其在一定范围内随机波动
y = randn(1, n);

% 绘制原始的点
figure;
plot(x, y, 'ro', 'MarkerSize', 5, 'LineWidth', 1);
hold on;

% 使用样条插值生成平滑曲线
xx = linspace(min(x), max(x), 1000);
yy = spline(x, y, xx);

% 绘制平滑曲线
plot(xx, yy, 'b-', 'LineWidth', 2);

% 设置图形属性
xlabel('X');
ylabel('Y');
title('随机点的平滑轨迹曲线');
grid on;
legend('原始点', '平滑曲线');
hold off;