简述
上一篇博文算法学习之SVD理论推导介绍了SVD矩阵分解的完整过程,感兴趣的可以去阅读一下。本文以图像为基础,利用SVD理论对二维图像矩阵进行分解,同时选取不同的特征值个数来对图像进行重构。主要使用OpenCV第三方视觉库完成SVD应用过程,原谅我这个调包小虾米。
使用OpenCV库的SVD功能API函数时,简短说一下SVD的分解矩阵,我们通过对图像矩阵 A A A( m × n m×n m×n,其中 m > n m>n m>n)表示分解为 U U U、 ∑ ∑ ∑、 V V V后,我们从对角矩阵 ∑ ∑ ∑中选取有限( k k k)个特征值保存,这些特征值对应的 U U U与 V V V中的一维向量 u i u_i ui与 v i v_i vi也对应保存,这样就可以用较少的特征值与特征向量来代表整个矩阵 A A A。
假设图像矩阵 A A A的完整表示如下:
A = σ 1 u 1 v 1 T + σ 2 u 2 v 2 T + ⋯ + σ n u n v n T A=σ_1 u_1 v_1^T+σ_2 u_2 v_2^T+⋯+σ_n u_n v_n^T A=σ1u1v1T+σ2u2v2T+⋯+σnunvnT
图像矩阵 A A A( m × n m×n m×n)其中 m > n m>n m>n, σ 1 , σ 2 , … , σ n σ_1,σ_2,…,σ_n σ1,σ2,…,σn特征值组成 ∑ ∑ ∑,同理 u 1 , u 2 , … , u n , … , u m u_1,u_2,…,u_n,…,u_m u1,u2,…,un,…,um组成为SVD分解矩阵 A A A的左边 U U U矩阵,其中 u 1 , u 1 , … , u n u_1,u_1,…,u_n u1,u1,…,un为非零特征向量, u n , … , u m u_n,…,u_m un,…,um为全零特征向量, v 1 T , v 2 T , … , v n T v_1^T,v_2^T,…,v_n^T v1T,v2T,…,vnT组成为SVD分解矩阵 A A A的右边 V T V^T VT矩阵。
那么,我们选取 k k k( k < n k<n k<n)个特征值与每个特征值对应的特征向量 u k u_k uk和 v k T v_k^T vkT来表示矩阵 A A A,公式如下:
A ≈ σ 1 u 1 v 1 T + σ 2 u 2 v 2 T + ⋯ + σ k u k v k T A≈σ_1 u_1 v_1^T+σ_2 u_2 v_2^T+⋯+σ_k u_k v_k^T A≈σ1u1v1T+σ2u2v2T+⋯+σkukvkT
实例代码
#include <iostream>
#include <opencv.hpp>
using namespace std;
using namespace cv;
int main(void)
{
Mat OriImg = imread("..//svd_example//data//lena_160w_100h.jpg", 0);
//Initialize the Matrix size equal to OriImg
Mat dstImg(OriImg.size(), CV_32FC1, Scalar(0));
OriImg.convertTo(OriImg, CV_32FC1);
// OpenCV求解出来的W特征值是一个一维向量,并不是SVD求解的对角矩阵,保存下来的只是特征值
Mat U, W, Vt;
// SVD Algorithms to Decomposed matrix
SVD::compute(OriImg, W, U, Vt, 4); // 调用SVD::compute()函数参数解释参考下面源码分析部分
// 初始化全为0的特征值矩阵
Mat EigenValueMatrix(OriImg.rows, OriImg.cols, CV_32FC1, Scalar(0));
//Set the features save percentages
const int features_nums = 50; // 设置保存的特征值个数
// 获取特征值并且存储为对角矩阵
for (int i = 0; i < features_nums; ++i)
{
EigenValueMatrix.ptr<float>(i)[i] = W.ptr<float>(i)[0];
}
cout << "OriImg Size is: " << OriImg.size() << endl;
cout << "U Size is: " << U.size() << endl;
cout << "EigenValueMatrix Size is: " << EigenValueMatrix.size() << endl;
cout << "V Size is: " << Vt.size() << endl;
// 图像矩阵进行重构
dstImg = U*EigenValueMatrix*Vt;
dstImg.convertTo(dstImg, CV_8UC1);
OriImg.convertTo(OriImg, CV_8UC1);
namedWindow("OriImg-window", 1);
imshow("OriImg-window", OriImg);
namedWindow("dstImg-window", 1);
imshow("dstImg-window", dstImg);
//imwrite("..//svd_example//data//oriImg.jpg", OriImg);
//imwrite("..//svd_example//data//svd_50.jpg", dstImg);
waitKey(0);
return 0;
}
实验结果与分析:
下面SVD实战应用代码读取的LENA图像的大小为 160 × 100 160×100 160×100的大小,如果对LENA图像矩阵全部保存的话,需要 160 × 100 = 16000 160×100=16000 160×100=16000个像素。
根据SVD分解公式,我们知道LENA图像分解出来的矩阵 U U U为 100 × 100 100×100 100×100,那么一个向量 u i u_i ui是 100 × 1 100×1 100×1的大小,同理矩阵 V V V为 160 × 160 160×160 160×160,那么其中一个向量 v i T v_i^T viT大小为 160 × 1 160×1 160×1。那么每一个特征值对应保存 1 + 100 + 160 = 261 1+100+160=261 1+100+160=261个像素。
假设我们选取特征值50个,那么我们需要保存的像素个数为 50 × 261 = 13050 50×261=13050 50×261=13050个像素。那么与存储原始图像矩阵 A A A对比,存储只需要原始图像矩阵 A A A的81%,这就是图像压缩保存过程。
我们来看一下选取不同的特征值个数重构图像显示的可视化结果(只需要修改上述代码中的features_nums=k值就可以得出下述的图像重构结果。):
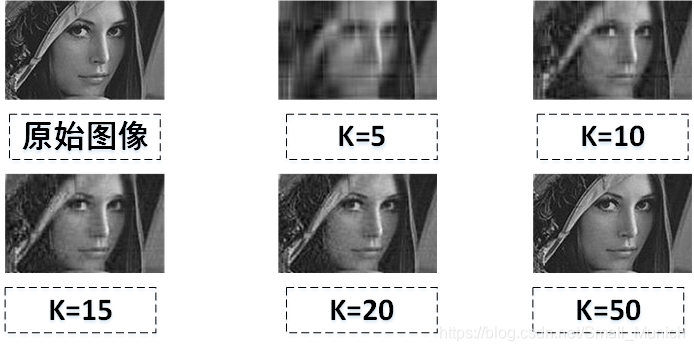
接下来就是贴出SVD类的接口API函数示例,可以直接查看OpenCV官网代码或者跳过这个环节至末尾查看一下SVD::compute()函数的API调用说明即可。
----------------------------------------------------华丽分割线-------------------------------------------
SVD源码API接口应用分析:
class CV_EXPORTS SVD
{
public:
enum Flags {
/** allow the algorithm to modify the decomposed matrix; it can save space and speed up
processing. currently ignored. */
MODIFY_A = 1,
/** indicates that only a vector of singular values `w` is to be processed, while u and vt
will be set to empty matrices */
NO_UV = 2,
/** when the matrix is not square, by default the algorithm produces u and vt matrices of
sufficiently large size for the further A reconstruction; if, however, FULL_UV flag is
specified, u and vt will be full-size square orthogonal matrices.*/
FULL_UV = 4
};
/** @brief the default constructor
initializes an empty SVD structure
*/
SVD();
/** @overload
initializes an empty SVD structure and then calls SVD::operator()
@param src decomposed matrix. The depth has to be CV_32F or CV_64F.
@param flags operation flags (SVD::Flags)
*/
SVD( InputArray src, int flags = 0 );
/** @brief the operator that performs SVD. The previously allocated u, w and vt are released.
The operator performs the singular value decomposition of the supplied
matrix. The u,`vt` , and the vector of singular values w are stored in
the structure. The same SVD structure can be reused many times with
different matrices. Each time, if needed, the previous u,`vt` , and w
are reclaimed and the new matrices are created, which is all handled by
Mat::create.
@param src decomposed matrix. The depth has to be CV_32F or CV_64F.
@param flags operation flags (SVD::Flags)
*/
SVD& operator ()( InputArray src, int flags = 0 );
/** @brief decomposes matrix and stores the results to user-provided matrices
The methods/functions perform SVD of matrix. Unlike SVD::SVD constructor
and SVD::operator(), they store the results to the user-provided
matrices:
@code{.cpp}
Mat A, w, u, vt;
SVD::compute(A, w, u, vt);
@endcode
@param src decomposed matrix. The depth has to be CV_32F or CV_64F.
@param w calculated singular values
@param u calculated left singular vectors
@param vt transposed matrix of right singular vectors
@param flags operation flags - see SVD::Flags.
*/
static void compute( InputArray src, OutputArray w,
OutputArray u, OutputArray vt, int flags = 0 );
/** @overload
computes singular values of a matrix
@param src decomposed matrix. The depth has to be CV_32F or CV_64F.
@param w calculated singular values
@param flags operation flags - see SVD::Flags.
*/
static void compute( InputArray src, OutputArray w, int flags = 0 );
/** @brief performs back substitution
*/
static void backSubst( InputArray w, InputArray u,
InputArray vt, InputArray rhs,
OutputArray dst );
/** @brief solves an under-determined singular linear system
The method finds a unit-length solution x of a singular linear system
A\*x = 0. Depending on the rank of A, there can be no solutions, a
single solution or an infinite number of solutions. In general, the
algorithm solves the following problem:
\f[dst = \arg \min _{x: \| x \| =1} \| src \cdot x \|\f]
@param src left-hand-side matrix.
@param dst found solution.
*/
static void solveZ( InputArray src, OutputArray dst );
/** @brief performs a singular value back substitution.
The method calculates a back substitution for the specified right-hand
side:
\f[\texttt{x} = \texttt{vt} ^T \cdot diag( \texttt{w} )^{-1} \cdot \texttt{u} ^T \cdot \texttt{rhs} \sim \texttt{A} ^{-1} \cdot \texttt{rhs}\f]
Using this technique you can either get a very accurate solution of the
convenient linear system, or the best (in the least-squares terms)
pseudo-solution of an overdetermined linear system.
@param rhs right-hand side of a linear system (u\*w\*v')\*dst = rhs to
be solved, where A has been previously decomposed.
@param dst found solution of the system.
@note Explicit SVD with the further back substitution only makes sense
if you need to solve many linear systems with the same left-hand side
(for example, src ). If all you need is to solve a single system
(possibly with multiple rhs immediately available), simply call solve
add pass #DECOMP_SVD there. It does absolutely the same thing.
*/
void backSubst( InputArray rhs, OutputArray dst ) const;
/** @todo document */
template<typename _Tp, int m, int n, int nm> static
void compute( const Matx<_Tp, m, n>& a, Matx<_Tp, nm, 1>& w, Matx<_Tp, m, nm>& u, Matx<_Tp, n, nm>& vt );
/** @todo document */
template<typename _Tp, int m, int n, int nm> static
void compute( const Matx<_Tp, m, n>& a, Matx<_Tp, nm, 1>& w );
/** @todo document */
template<typename _Tp, int m, int n, int nm, int nb> static
void backSubst( const Matx<_Tp, nm, 1>& w, const Matx<_Tp, m, nm>& u, const Matx<_Tp, n, nm>& vt, const Matx<_Tp, m, nb>& rhs, Matx<_Tp, n, nb>& dst );
Mat u, w, vt;
};
我们知道类SVD里面有对应的功能函数与静态函数,下面我们对一些函数调用简单说明一下:
static void compute( InputArray src, OutputArray w, OutputArray u, OutputArray vt, int flags = 0 );
SVD::compute()函数是本篇调用的主要函数,里面的参数简单介绍一下:
src: 输入图像矩阵;
w: 输出特征值矩阵,只不过是一维向量保存所有特征值,并不是SVD分解后以对角矩阵形式保存;
u: 输出矩阵,SVD分解矩阵特征值矩阵左边的U矩阵;
vt:输出矩阵,SVD分解矩阵特征值矩阵右边的V矩阵转置;
flags: 输入的标志,有3种枚举情况;如果我们的输入矩阵src不是方阵,即行列不等,建议使用FULL_UV,这样调用compute()函数输出的U、V矩阵是单位正交矩阵;
这里强调一下,①如果输入图像的宽高不等,SVD分解调用compute()函数的flags采取默认的方式,在进行图像重构时候会报错;②记得要将输入图像的深度改为CV_32F或者CV_64F形式;
参考
https://docs.opencv.org/4.0.0-beta/d2/de8/group__core__array.html#gab477b5b7b39b370bb03e75b19d2d5109







 本文介绍了如何使用OpenCV库中的SVD(奇异值分解)功能对图像矩阵进行分解和重构。通过选取不同数量的特征值,展示了如何减少图像存储需求并实现图像压缩。SVD::compute()函数的使用和注意事项也在文中进行了说明。
本文介绍了如何使用OpenCV库中的SVD(奇异值分解)功能对图像矩阵进行分解和重构。通过选取不同数量的特征值,展示了如何减少图像存储需求并实现图像压缩。SVD::compute()函数的使用和注意事项也在文中进行了说明。
















 9588
9588

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








