算法的复杂度分析

1 算法效率的度量

1.1 算法效率度量的方法

思考：如果两个算法都满足功能性需求，那工程中最关心的其它特性是什么？如何比较评判呢？

注意：性价比（比率）是工程中最关注的算法附件特性！

算法效率度量的方法主要分为两种：事后统计法和事前分析估算法。

1.2 事后统计法

比较不同算法对同一组输入数据的运行处理时间。

缺陷：

• 为了获得不同算法的运行时间必须编写相应程序。
• 运行时间严重依赖硬件以及运行时的环境因素。
• 算法的测试数据的选取相当困难。

事后统计法不容易准确度量算法的效率。

1.3 事前分析估算法

依据统计的方法对算法效率进行估算。

影响算法效率的主要因素：

1. 算法采用的策略和方法。
2. 问题的输入规模。
3. 编译器所产生的代码。
4. 计算机执行速度。

事前分析估算法通过操作数量度量算法效率。

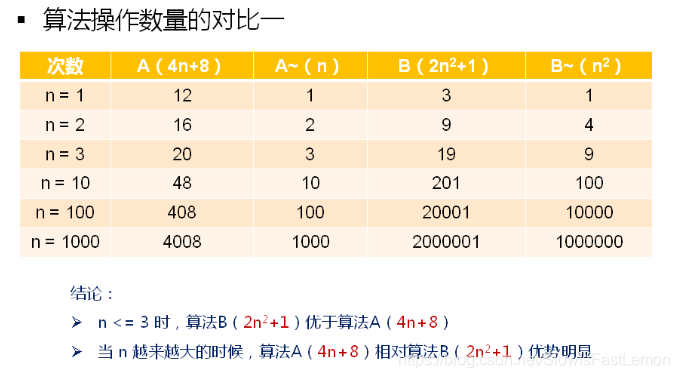
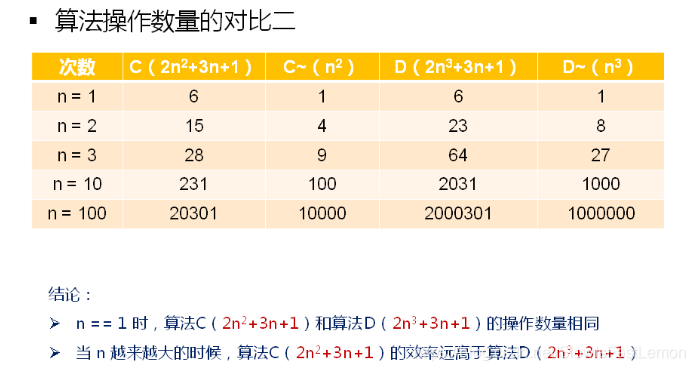
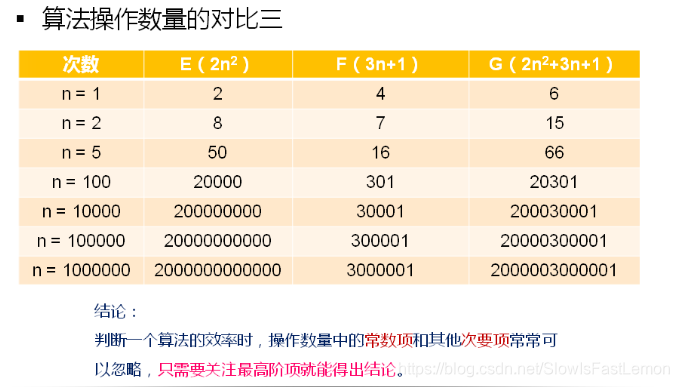
判断一个算法效率时只需要关注最高阶项就能得出结论。某个算法，随着问题规模n的增大，它会越来越优于另一个算法，或者越来越差于另一个算法。

结论：判断一个算法的效率时，操作数量中的常数项和其他次要项常常可以忽略，只需要关注最高阶项就能得出结论。

---

2 算法的复杂度

2.1 算法的复杂度

问题：如何用符号定性的判断算法的效率？

算法的复杂度：

• 时间复杂度：算法运行后对事件需求量的定性描述。
• 空间复杂度：算法运行后对空间需求量的定性描述。

注意：

• 数据结构课程重点关注的是算法的效率问题，因此，整个课程会集中于讨论算法的时间复杂度；但其使用的方法完全可以用于空间复杂度的判断！

2.2 算法的时间复杂度

时间复杂度是算法运行时对于时间的需求量，大O表示法用于描述算法的时间复杂度，大O表示法只关注操作数量的最高次项。

大O表示法：

• 算法效率严重依赖于操作（Operation）数量。
• 操作数量的估算可以作为时间复杂度的估算。
• 在判断时首先关注操作数量的最高次项。
  
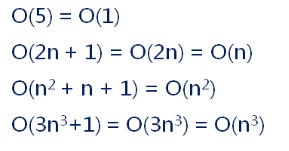
  常见的时间复杂度如下：
  
  
  
  常见的时间复杂度列出如下：
  
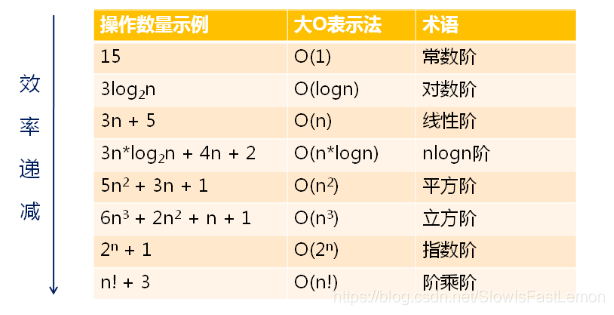
  常见的时间复杂度的比较：
  
  一般而言，工程中使用的算法，时间复杂度不超过O(n^3)。

算法分析示例：

算法的最好与最坏情况：

• 当算法在最坏情况下仍然能满足需求时，可以推断，算法的最好情况和平均情况都满足需求。
• 一般情况下，如果没有特殊说明，我们所分析算法的时间复杂度都是指最坏时间复杂度。

2.3 算法的空间复杂度

算法的空间复杂度（Space Complexity）：

• 定义：S(n) = S(f(n))
  • n为算法的问题规模。
  • f(n)为空间使用函数，与n相关。

推到时间复杂度的方法同样适用于空间复杂度，例如：当算法所需要的空间是常数时，空间复杂度为S(1)。

空间复杂度计算示例：

空间与时间的策略：

• 多数情况下，算法的时间复杂度更令人关注。
• 如果有必要，可以通过增加额外空间降低时间复杂度。
• 同理，也可以通过增加算法的耗时降低空间复杂度。

实例分析：空间换时间

/*
    问题： 
    在一个由自然数1-1000中某些数字所组成的数组中，每个数字可能出现零次或者多次。
    设计一个算法，找出出现次数最多的数字。
*/

#include <iostream>

using namespace std;

void search(int a[], int len)     // O(n)
{
    int sp[1000] = {0};
    int max = 0;
    
    for(int i=0; i<len; i++)
    {
        sp[a[i] - 1]++;
    }
    
    for(int i=0; i<1000; i++)
    {
        if( max < sp[i] )
        {
            max = sp[i];
        }
    }
    
    for(int i=0; i<1000; i++)
    {
        if( max == sp[i] )
        {
            cout << i + 1 << endl;
        }
    }
}

int main(int argc, char* argv[])
{
    int a[] = {1, 1, 3, 4, 5, 6, 6, 6, 3, 3};
    
    search(a, sizeof(a)/sizeof(*a));

    return 0;
}

面试题：当两个算法的大O表示法相同时，是否意味着两个算法的效率完全相同？

• 不相同，只是在一个数量级上。

---

参考资料：

1. 数据结构实战开发教程