【四旋翼无人机】基于PI控制器的四旋翼无人机飞行控制simulink建模与仿真

目录

1.算法仿真效果

2.MATLAB程序

3.算法概述

4.部分参考文献

5.程序内容，运行方法和源码获取

5.1 作品内容 

5.2 运行方法

5.3 源码获取

---

1.算法仿真效果

Matlab2024b仿真结果如下：

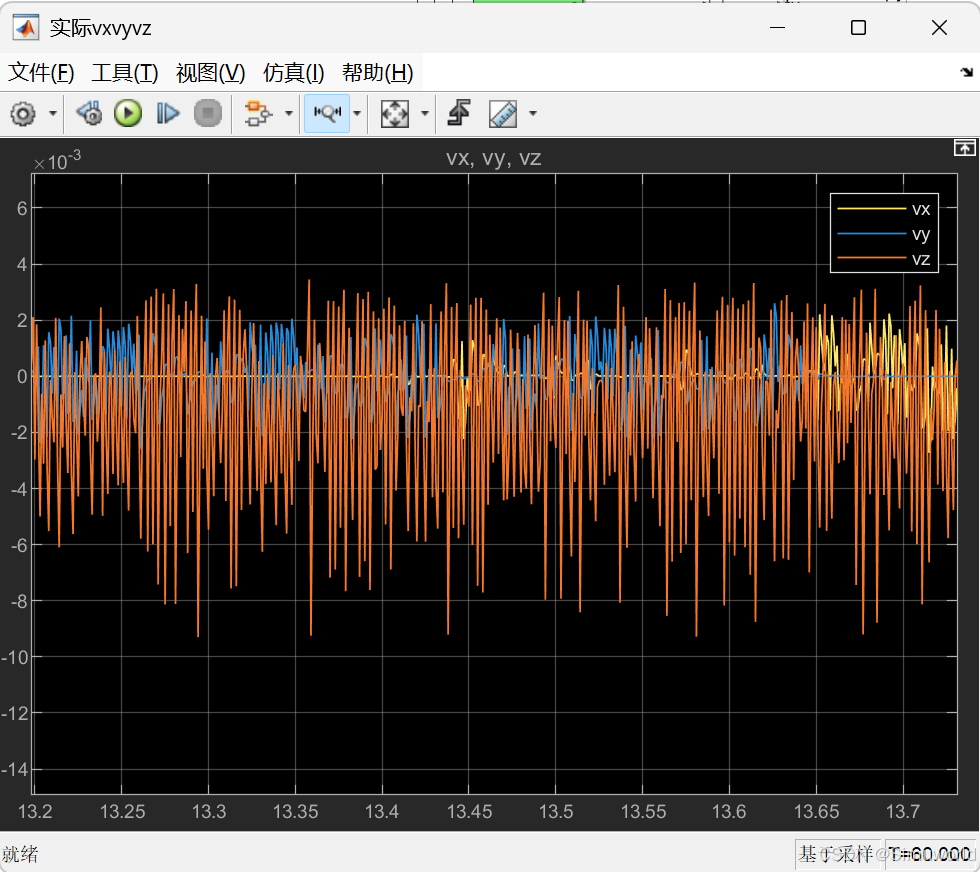
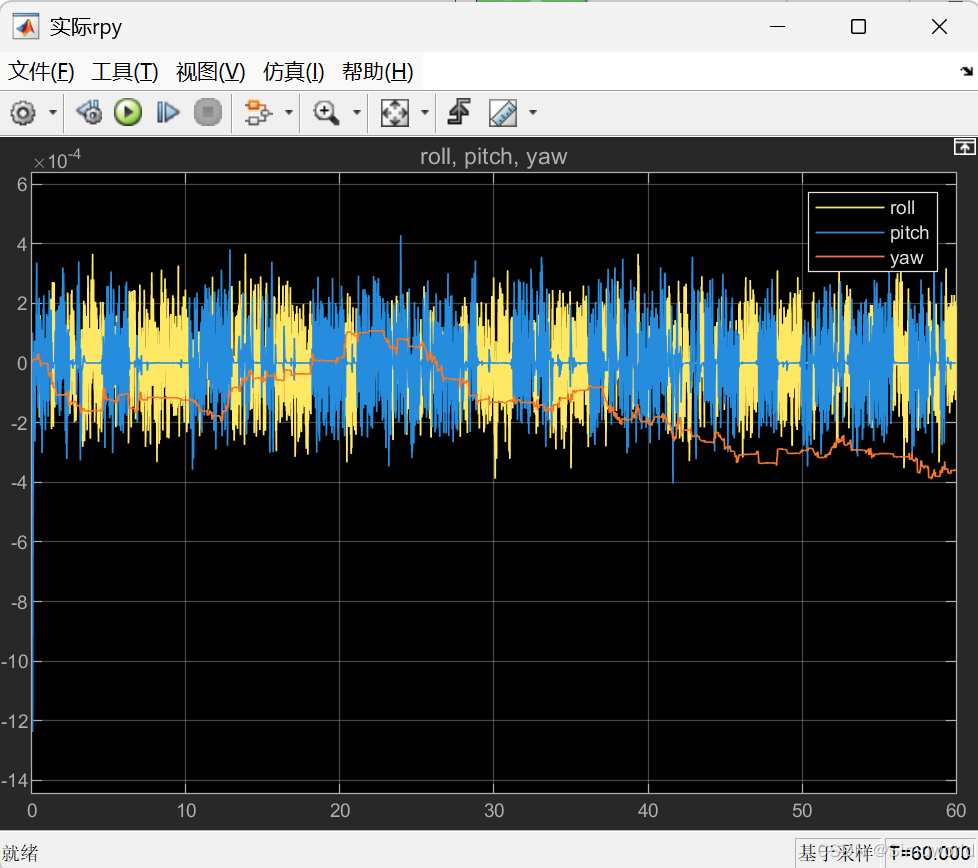
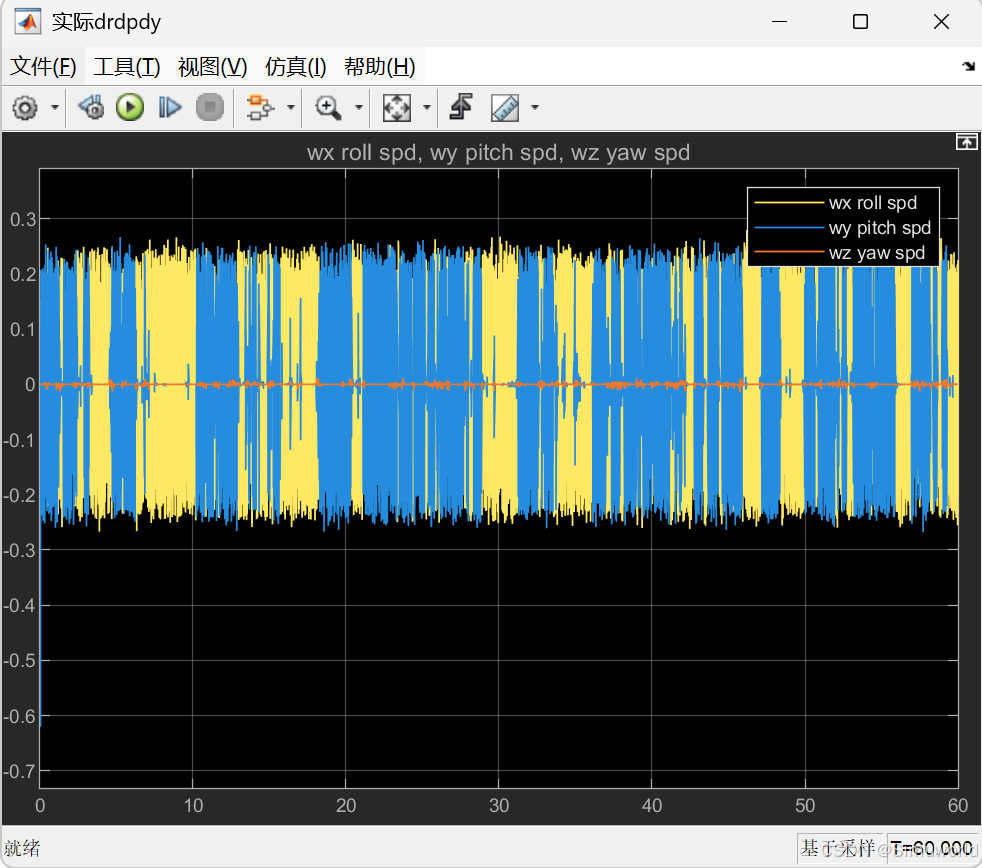
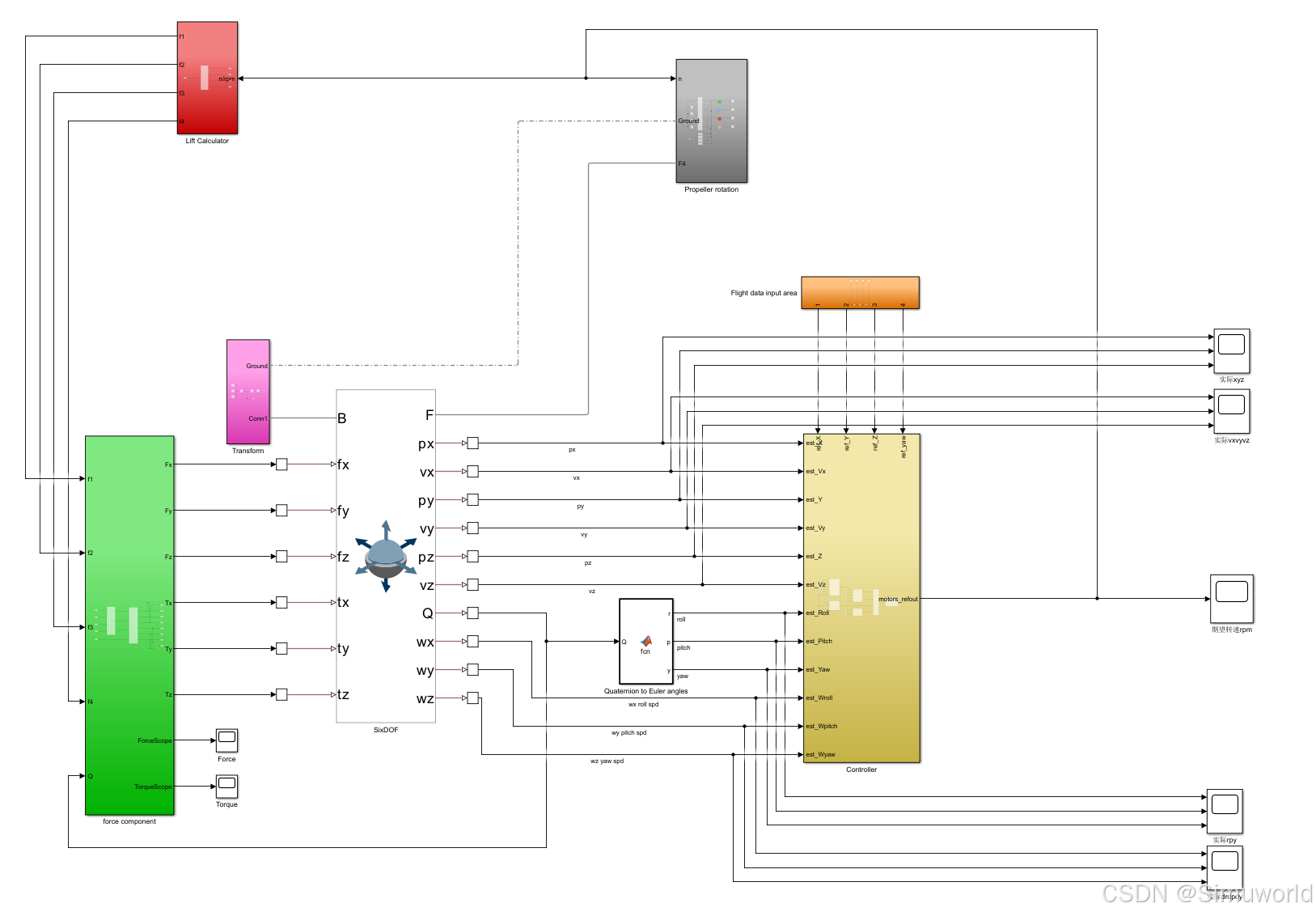
2.MATLAB程序

%旋转关节（RevoluteJoint）参数配置 =============%
% 旋转关节用于定义两个刚体之间的旋转自由度，此处仅配置Z轴旋转（Rz）的初始位置（Pos）
% 其他旋转轴（Rx/Ry）和移动轴（Px/Py/Pz）等未配置，说明模型中关节仅允许绕Z轴旋转
% 初始化RevoluteJoint结构体数组：先为第4个元素填充空值（占位）
% 结构体包含2个字段：Rz.Pos（Z轴旋转初始位置）、ID（关节标识，对应两个刚体的连接关系）
smiData.RevoluteJoint(4).Rz.Pos = 0.0;
smiData.RevoluteJoint(4).ID = '';
% 第1个旋转关节：定义基座与顺时针桨叶（1-2）的连接关节
smiData.RevoluteJoint(1).Rz.Pos = -89.999999999999986;  % deg
smiData.RevoluteJoint(1).ID = '[base_fight_first2-3:-:55mm_paddle_clockwise - 1-2]';
% 第2个旋转关节：定义基座与顺时针桨叶（3-2）的连接关节
smiData.RevoluteJoint(2).Rz.Pos = -89.999999999999986;  % deg
smiData.RevoluteJoint(2).ID = '[base_fight_first2-3:-:55mm_paddle_clockwise - 3-2]';
% 第3个旋转关节：定义基座与逆时针桨叶（2-2）的连接关节
smiData.RevoluteJoint(3).Rz.Pos = -89.999999999999986;  % deg
smiData.RevoluteJoint(3).ID = '[base_fight_first2-3:-:55mm_paddle_counter_clock - 2-2]';
% 第4个旋转关节：定义基座与逆时针桨叶（4-2）的连接关节（补全初始化的空值）
smiData.RevoluteJoint(4).Rz.Pos = -89.999999999999986;  % deg
smiData.RevoluteJoint(4).ID = '[base_fight_first2-3:-:55mm_paddle_counter_clock - 4-2]';
24

3.算法概述

      四旋翼无人机通过4个电机驱动螺旋桨产生升力，电机按“对角同向、邻角反向”布置（如图1）：电机 1（前左）、3（后右）顺时针旋转，电机2（前右）、4（后左）逆时针旋转，抵消单电机旋转产生的反扭矩。其运动依赖升力差和力矩差实现6个自由度（3个位置：x/y/z；3个姿态：滚转φ/ 俯仰θ/偏航ψ）控制：​

垂直运动（z 轴）：4个电机升力之和变化（升力＞重力时上升，反之下降）；​

滚转运动（φ 角）：左右电机升力差产生滚转力矩（左电机升力增大、右电机减小→机身左倾）；​

俯仰运动（θ 角）：前后电机升力差产生俯仰力矩（前电机升力增大、后电机减小→机身前倾）；​

偏航运动（ψ 角）：反向电机阻力矩差产生偏航力矩（顺转电机阻力矩增大、反转电机减小→机身顺时针旋转）；​

水平运动（x/y 轴）：通过滚转/俯仰改变升力在水平方向的分量（如前倾角θ→升力分解出x向分力，推动机身前进）。

       控制目标是使无人机跟踪期望位置（​xd​,yd​,zd​）和期望姿态（​φd​,θd​,ψd​），核心矛盾是非线性强耦合（如 x 向运动依赖 θ 角，y 向运动依赖 φ 角）和外部扰动（风、负载变化）。PI 控制器通过 “比例项快速响应误差、积分项消除静差”，成为解决该问题的基础方案。

4.部分参考文献

[1]郝瑞阳,马文涛,陈希银.四旋翼飞控系统设计与仿真[J].福建电脑, 2024, 40(7):81-85.

5.程序内容，运行方法和源码获取

5.1 作品内容 

matlab程序,Simulink模型

5.2 运行方法

1.在matlab的左侧的当前文件夹窗口；

2.运行para.m文件，再运行models.slx模型文件。

5.3 源码获取

step1.打开博客主页的左侧推广栏查看，或扫博客文章底部信息

step2.然后用电脑打开网页链接，输入文章标题搜索