【薄板样条】基于TPS薄板样条的图像几何形状变换算法

目录

1.算法仿真效果

2.MATLAB程序

3.算法概述

4.部分参考文献

5.程序内容，运行方法和源码获取

5.1 作品内容 

5.2 运行方法

5.3 源码获取

---

1.算法仿真效果

matlab2022a/Matlab2024b仿真结果如下：

2.MATLAB程序

................................................................
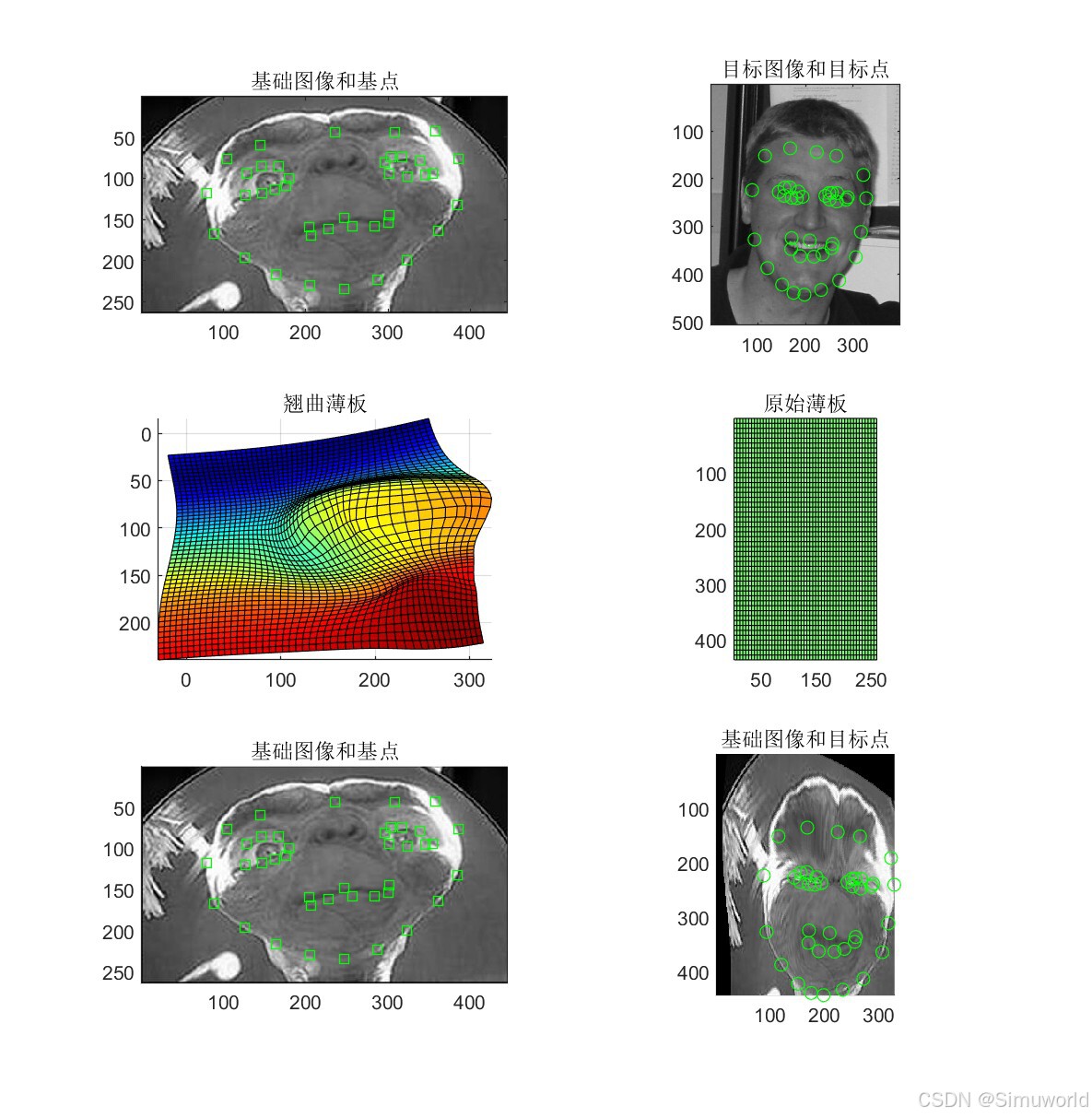
% 显示变换后的薄板样条网格
subplot(M, N, I, 'align'); I = I+1;
% 计算网格点的位移量
g = sqrt((grid_x - wgrid_x).^2 + (grid_y - wgrid_y).^2);

% 绘制变换后的网格
surf(wgrid_x, wgrid_y, g);
view(2);  % 设置视角为俯视图
axis image ij;  % 设置坐标轴属性，保持图像比例
title('翘曲薄板');  % 设置子图标题

% 显示原始薄板样条网格
subplot(M, N, I, 'align'); I = I+1;
% 计算网格点的位移量（此处为0，用于可视化原始网格）
g = sqrt((grid_x - grid_x).^2 + (grid_y - grid_y).^2);

% 绘制原始网格
surf(grid_x, grid_y, g);
view(2);  % 设置视角为俯视图
axis image ij;  % 设置坐标轴属性，保持图像比例
title('原始薄板');  % 设置子图标题

% 再次显示源图像和源特征点
subplot(M, N, I, 'align'); I = I+1;
hold on;
imagesc(img); colormap gray;  % 以灰度图方式显示图像
plot(ipts(:,1), ipts(:,2), 'gs');  % 绘制源特征点
axis image ij;  % 设置坐标轴属性，保持图像比例
title('基础图像和基点');  % 设置子图标题

% 显示变换后的图像和目标特征点
subplot(M, N, I, 'align'); I = I+1;
hold on;
imagesc(wimg);  % 显示变换后的图像
plot(opts(:,1), opts(:,2), 'go');  % 绘制目标特征点
axis image ij;  % 设置坐标轴属性，保持图像比例
title('基础图像和目标点');  % 设置子图标题

% 设置颜色映射为jet（彩虹色）
colormap jet;
30

3.算法概述

TPS的数学推导基于最小化薄板弯曲能量，其能量函数定义为：

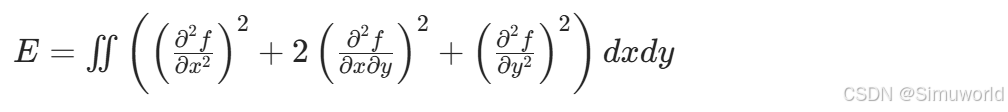
       通过变分法求解能量最小化问题，可推导出TPS的插值条件：对于每个控制点(xi​,yi​)，其变换后的坐标(ui​,vi​)需满足f(xi​,yi​)=ui​和g(xi​,yi​)=vi​（分别对应x和y方向的变换函数）。

步骤 1：控制点选取与对应关系建立

步骤 2：构建TPS插值方程组

对于二维变换，需分别求解x方向和y方向的变换函数。以x方向为例，构建方程组：

步骤3：求解系数矩阵

       上述方程组为线性方程组，可通过矩阵求逆或数值方法（如QR分解、SVD分解）求解w和a。以分块矩阵求逆:

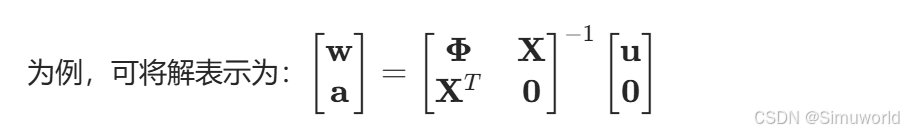
       实际计算中，由于矩阵规模随控制点数量增长，需注意数值稳定性，通常采用正则化方法（如添加小量λI到Φ中）避免矩阵奇异。

步骤 4：定义变换函数

对于源图像中任意点(x,y)，其变换后的坐标(u,v)可通过以下公式计算：

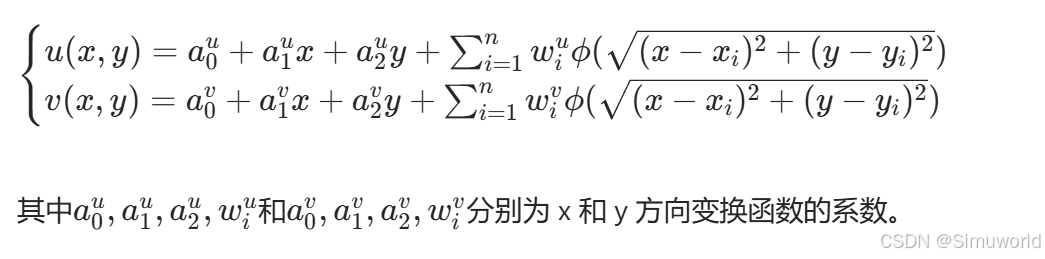
步骤5：图像重采样与变换实现

得到变换函数后，需对源图像进行重采样：

4.部分参考文献

[1]孙冬梅,裘正定.利用薄板样条函数实现非刚性图像匹配算法[J].电子学报, 2002, 30(8):1104-1107.DOI:10.3321/j.issn:0372-2112.2002.08.003.

[2]吴月娥,王小喜,哈章,等.基于薄板样条和形状内容的医学图像非刚性配准方法研究[J].航天医学与医学工程, 2007, 20(1):4.DOI:10.3969/j.issn.1002-0837.2007.01.010.

5.程序内容，运行方法和源码获取

5.1 作品内容 

matlab程序

5.2 运行方法

1.在matlab的左侧的当前文件夹窗口；

2.运行Runme文件；

5.3 源码获取

step1.打开博客主页的左侧推广栏查看，或扫博客文章底部信息

step2.然后用电脑打开网页链接，输入文章标题搜索