UDIS++——薄板样条插值TPS——公式推导

是一种插值方法，薄板样条是一维三次样条的二维模拟。

薄板样条插值（Thin Plate Spline, TPS）是一种基于物理启发的非刚性插值方法，广泛应用于图像配准、几何变形和曲面拟合等领域。其核心思想是通过最小化弯曲能量（Bending Energy）来实现平滑插值。以下是其公式的详细推导过程：

---

1. 问题定义与目标函数

假设给定 N 个控制点 目标是找到一个光滑的映射函数 f(x,y)，满足：

同时最小化弯曲能量，即：

---

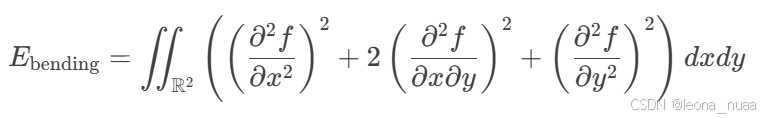
2. 弯曲能量的物理意义

弯曲能量 是薄金属板在外力作用下变形的物理模型的数学抽象：

• 一阶导数描述平移，二阶导数描述曲率。

• 最小化弯曲能量等价于寻找“最平滑”的变形表面。

---

3. 薄板样条的解形式

TPS 的解由 仿射变换（全局线性部分）