图像拼接-核心技术-薄板样条插值TPS（Thin Plate Spline）

小容的技术栈

已于 2025-05-13 15:46:55 修改

阅读量2.4k

点赞数 45

分类专栏：图像拼接文章标签： python pytorch

于 2024-10-13 10:08:40 首次发布

本文链接：https://blog.youkuaiyun.com/weixin_51949030/article/details/142894317

版权

图像拼接专栏收录该内容

1 篇文章

订阅专栏

一，原理

1，数学解释

是一种插值方法，薄板样条是一维三次样条的二维模拟。给定一组数据点，以每个数据点为中心的薄板样条的加权组合给出了通过这些点的插值函数正是在最小化所谓的“弯曲能量”的同时。弯曲能量这里定义为二阶导数平方的积分R2

（给定L个点以及他们对应的函数值. TPS插值的目标就是求解一个函数，使得,并且弯曲能量函数最小。我们把插值函数想象成用力去弯折一块薄钢板，使这块钢板穿过给定的L个点，弯曲这块钢板所需的力或者能量可以表示为）

2，TPS进行坐标变换

概述：使用两个样条函数,一个用于位移在x方向和y方向上的位移。每个方向上的位移被认为是一个点的高度映射（高度图），并且在三维空间中离散点的情况下拟合样条，最后，将两个结果转换组合为单个映射。

每个方向(X , Y)的位移(ΔX,ΔY)可以被视为N个点高度图(height map), 因此样条的就像在3D空间拟合散点(scatter point) 一样, 如下图所示

样条函数形式如下：

我们定义的两个样条函数分别是：

解释：其中前三个系数(a1,ax,ay)表示能通过所有控制点(xi,yi)最逼近x'（或y'）的线性平面，𝑤𝑖表示每个控制点的控制权重，U(||((xi,yi)−(x,y))||)表示核函数，||U()||表示L1范式

薄板样条核U(r)=r2log(r)，接受的参数为待移动点与控制点的距离||((xi,yi)−(x,y))||，待变换点离内核中心(控制点)越近，它的高度或返回值就越高。薄板样条核可视化如下图所示：

为了使样条函数f(x,y)有平方可积的二阶导数,添加了一个约束，如下图：

解释：第一个确保施加到板上的载荷和为零，使板不会上下移动；后两个相对于x轴y轴力矩为零，使曲面不旋转。

3，求解过程

每个薄板样条函数的系数(𝑎,𝑎𝑥,𝑎𝑦,𝑤𝑖),结合f(xi,yi)=vi,可由线性系统解出：

解释1：其中Kij=U(||(xi,yi),(xj,yj)||)，P的第i行是齐次表示(1,xi,yi)组成，𝑣是所有控制点组成的向量，w是由wi构成的列向量，O是3x3的全0矩阵, o是3x1的全0列向量, a是由[a1 , ax , ay ] 组成的列向量。

解释2：第一行[K P]×[v,o]T[𝐾 𝑃]×[𝑣,𝑜]𝑇表示由所有(xi,yi)(𝑥𝑖,𝑦𝑖)替代得到的函数fx′𝑓𝑥′或fy′

第二行[PT O][𝑃𝑇， 𝑂]表示系统的额外约束，见概述部分。

以N=3(控制点数量为3)为例，可得到如下的线性系统：

上文写错了，应该是K矩阵里面包含U11,U12,U13….U33,把上文的含K11,K12,K13….K33，替换为U11,U12,U13….U33,。

由LW=Y解得W矩阵，能得到相应的[ w a ]。

原文链接：https://blog.youkuaiyun.com/g11d111/article/details/128641313

二，TPS在论文UDIS++中的应用

1，论文中使用原理

（1）.将平面图像上的N个控制点记为P = [ p1 , ... , pN]T

翘曲图像上的对应点记为P′= [ p′1 , ... , p′N]T ( pi , p′i∈R2 × 1)。

通过最小化一个由数据项和畸变项组成的能量函数[ 20 ] (详见补充材料第2.1节)，TPS变换可以参数化为式( 2 )：

式中：p为平面图像上的任意一点，p′为翘曲图像上的对应点。

C∈R2 × 1，M∈R2 × 2，wi∈R2 × 1为变换参数。

O ( r ) = r2logr2是径向基函数，表示每个控制点对p的影响。(薄板样条核)

||O(pi)||表示L2范数，表示向量元素的平方和再开方。

（2）.为了求解这些参数，我们根据方程2使用N对控制点制定N个数据约束，并施加额外的维度约束[ 20 ]，如方程3所述：

（3）.这些约束可以改写为矩阵计算的形式，参数可以如下求解：

其中1是一个N × 1的All - One矩阵，

K∈RN × N中的每个元素kij由O(∥pi-pj∥2)确定，

且W = [ wi , ... , wN]T。

（4）.目标是使用具有最小曲率的薄板。然后，我们建立了一个能量优化问题，该问题同时涉及对齐和失真，

式中：λ为平衡因子，用于控制经纱的光滑度。对准能量和失真能量定义如下：

式中：T ( · )为翘曲函数。当λ > 0时，允许控制点发生轻微的错位，以产生畸变较小的翘曲。

式中：T ( · )为翘曲函数。当λ > 0时，允许控制点发生轻微的错位，以产生畸变较小的翘曲。然而，在我们的实现中，我们设置λ = 0来强约束控制点的运动。这意味着我们的网络预测了控制点的运动，并强制实际运动( T ( p ) -p )与预测运动相等。通过最小化Eq . 14，我们可以确定翘曲函数，推导如下(见公式5）：

2，代码实现

一.求参数矩阵

（1）构建在宽维度的all-one矩阵和P的拼接。[1 P]

num_batch  = source.size()[0]
num_point  = source.size()[1]
ones = torch.ones(num_batch, num_point, 1).float()
if torch.cuda.is_available():
    ones = ones.cuda()
p = torch.cat([ones, source], 2) # [bn, pn, 3]

（2）计算矩阵K。薄板样条核O(r)=r2log(r)，接受的参数为待移动点与控制点的距离||p−pi||2，代码如下。

p_1 = p.reshape([num_batch, -1, 1, 3]) #[bn, pn, 1, 3]
p_2 = p.reshape([num_batch, 1, -1, 3])  #[bn, 1, pn, 3]
d2 = torch.sum(torch.square(p_1-p_2), 3) # p1 - p2: [bn, pn, pn, 3]   final output: [bn, pn, pn]

#计算权重 r，根据距离平方 d2 计算权重 r 
r = d2 * torch.log(d2 + 1e-6) # [bn, pn, pn]

（3）构建矩阵W并求逆得到右1矩阵。[1 P]和K在宽维度拼接，all-zero矩阵和[1 P]的转置矩阵在宽维度拼接

zeros = torch.zeros(num_batch, 3, 3).float()
if torch.cuda.is_available():
    zeros = zeros.cuda()
W_0 = torch.cat((p, r), 2) # [bn, pn, 3+pn]
W_1 = torch.cat((zeros, p.permute(0,2,1)), 2) # [bn, 3, pn+3]
W = torch.cat((W_0, W_1), 1) # [bn, pn+3, pn+3]
W_inv = torch.inverse(W.type(torch.float64))

（4）构建矩阵tp得到右2矩阵

zeros2 = torch.zeros(num_batch, 3, 2)
if torch.cuda.is_available():
    zeros2 = zeros2.cuda()
tp = torch.cat((target, zeros2), 1) # [bn, pn+3, 2]

（5）计算参数矩阵

T = torch.matmul(W_inv, tp.type(torch.float64)) # [bn, pn+3, 2]
T = T.permute(0, 2, 1) # [bn, 2, pn+3]

三，TPS在ELA中的应用

1，拼接流程

给定两幅重叠图像Ip和Iq及其匹配点pi = ( xi , yi)T，qi = ( ui , vi)T，i = 1，· · ·，n，可以利用DLT [ 34 ]或AutoStitch [ 4 ]的方法估计Ip和Iq之间的全局变换。

2，论文中使用原理

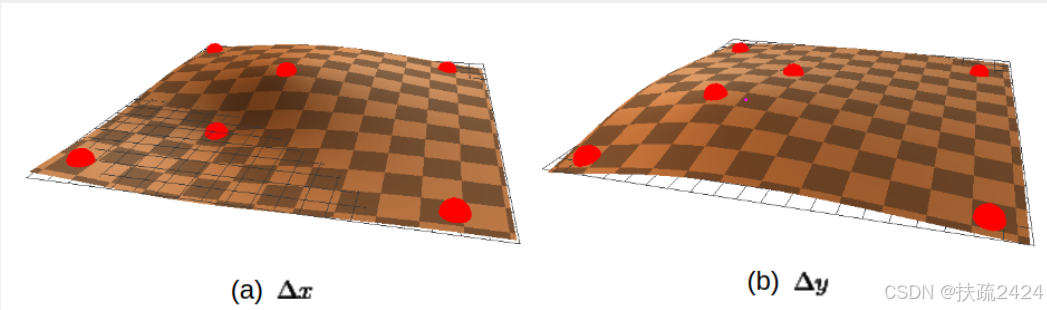
图像Iq的形变可以表示为G( x , y) = ( g ( x , y ))，h( x , y) ) T，其中g( x , y)和h( x , y)分别是x和y方向的形变。为简便起见，在后面的分析中，我们使用g ( x , y)代替G( x , y)，因为g ( x , y)和h ( x , y)的计算完全相同且相互独立。

图3 .变形函数。图( a )和( b )是给定散射偏差gi的形变函数G( x , y) = ( g ( x , y ))，h( x , y) ) T的两个分量。

最优经向能量函数包含两项：对齐项JD和平滑项JS，定义为

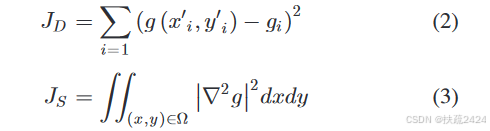
待最小化的总体能量函数为

式中：λ为加权参数，用于平衡两项。根据TPS的基本理论[ 26 ]，最小化问题( 4 )的最优解可以表示为

其中φ i ( x ) = | x-p′i | 2 ln | x-p′i |是径向基函数.系数w = ( ω1 , · · · ωn)T和a = ( α1 , α2 , α3)T可以通过求解下面的线性系统来计算

其中C2，2 = 8 π为常数，K = ( φi ( p′j ) )∈Rn × n，P = ( ( p′1 , · · · , ( p′n ))T∈Rn × 3，f = ( g1 , · · · , gn)T . ( 5 )当匹配数n≥4时有唯一解[ 26 ] .将w和a代入式( 5 )可以得到源图像中任意位置( x , y)T的形变。

为了加速计算，在图像平面上设置了均匀的Cx × Cy细胞网格。变形首先在网格节点上计算，然后线性插值到所有其他像素。对于图1所示的输入图像，计算得到的形变函数如图3所示。根据计算得到的变形量g ( x , y)，可以对Iq进行翘曲处理，以消除与Ip的不对齐。网格变形场的一个例子如图2 ( b )所示。