全球名校AI课程库（26）| MIT麻省理工 · 计算机科学的数学基础课程『Mathematics for Computer Science』

🏆 课程学习中心 | 🚧 CS数学基础课程合辑 | 🌍 课程主页 | 📺 中英字幕视频 | 🚀 项目代码解析

课程介绍

数学几乎是“艰难”与“枯燥”的同义词了，定理、推导，做题、考试，大脑的催眠药，意志力的催残剂。但数学又是如此重要，当绕过了它选择了工科，却发现每一项重要的应用背后都需要它的支撑。学习计算机，不管是基本的程序逻辑还是进阶的算法，都依托于某一项数学知识。

但是！数学又是一门无穷尽的学科，知识点与分支蜿蜒绵长。但CS的宝宝们，你们并不需要抱着数学书去啃！世界top大学有高招，比如！MIT 6.042J 就根据计算机方向所需的知识，对数学做了一个梳理打包，通过有趣的方式，让你快速构建CS所需最小数学知识根基！

MIT 6.042J 是顶级院校麻省理工出品的工科基础优质课程，围绕计算机科学方向，构建所需的数学体系内容，包含函数、离散数学、概率论、图和树结构，以及部分算法（例PageRank）。不同于枯燥的理论数学，本课程的数学知识都有计算机科学方向的延展应用，是工科方向同学值得一学的基础课程。

课程讲师 Albert R Meyer 是麻省理工 Department of Electrical Engineering and Computer Science （电气工程和计算机科学系）的教授。

课程主题

课程覆盖范围大致分为三部分。学完完成6.042J后，你能够解释和应用计算机科学中离散(非连续)数学的基本方法，并在算法设计和分析、可计算理论、软件工程、计算机系统等领域得到充分应用。

• 数学的基本概念：定义、证明、集合、函数、关系
• 离散结构：图，状态机，模运算，计数
• 离散概率理论

课程资料

公✦众✦号回复关键字 🎯『6.042J』，就可以获取整理完整的资料合辑啦！当然也可以点击 🎯 这里 查看更多课程的资料获取方式！

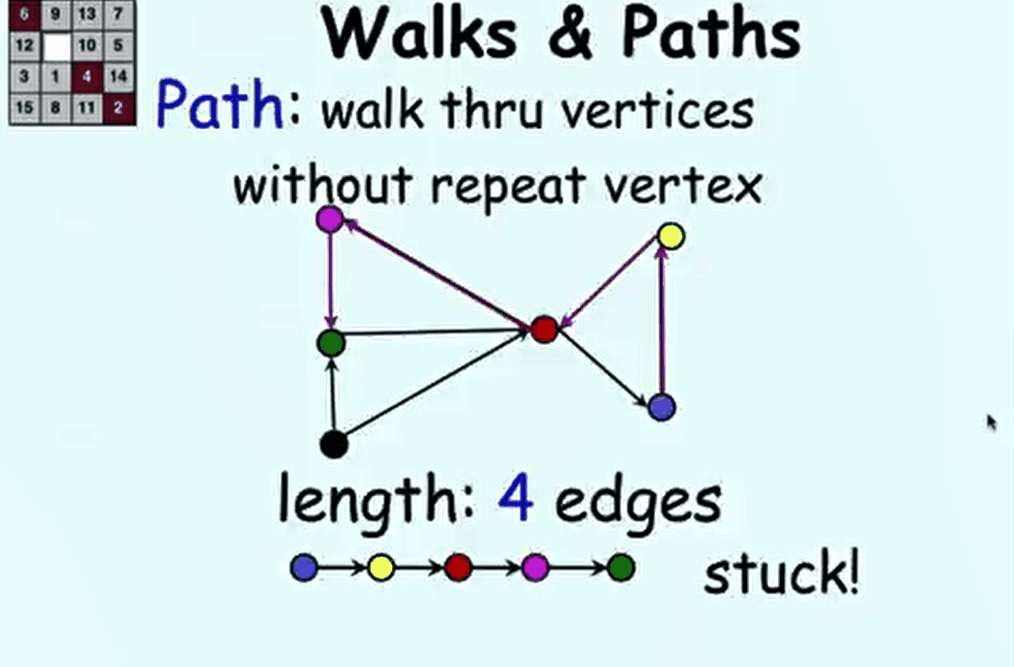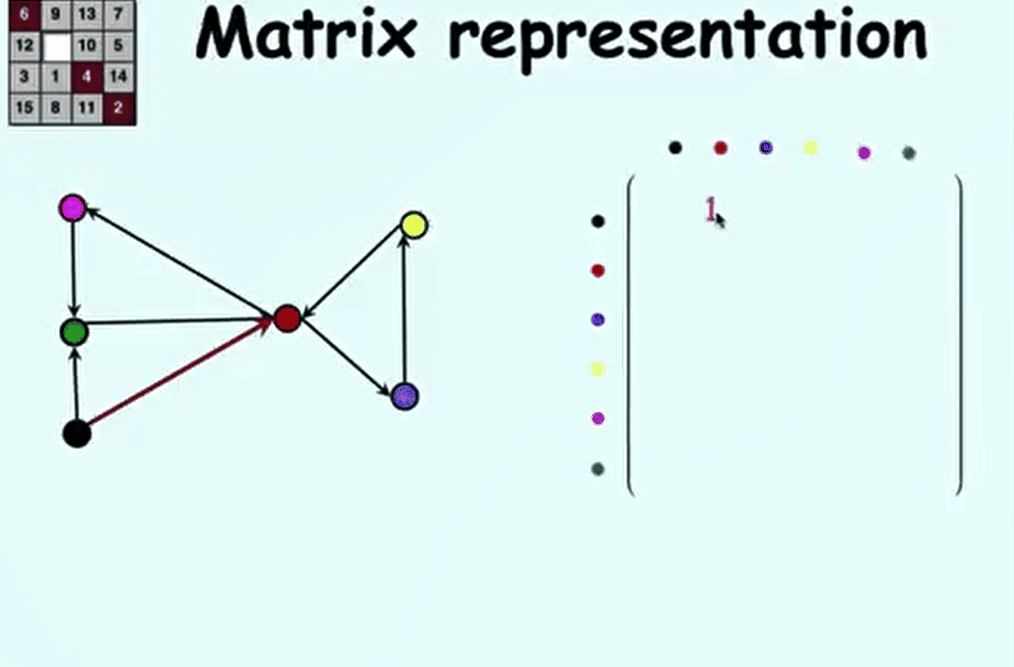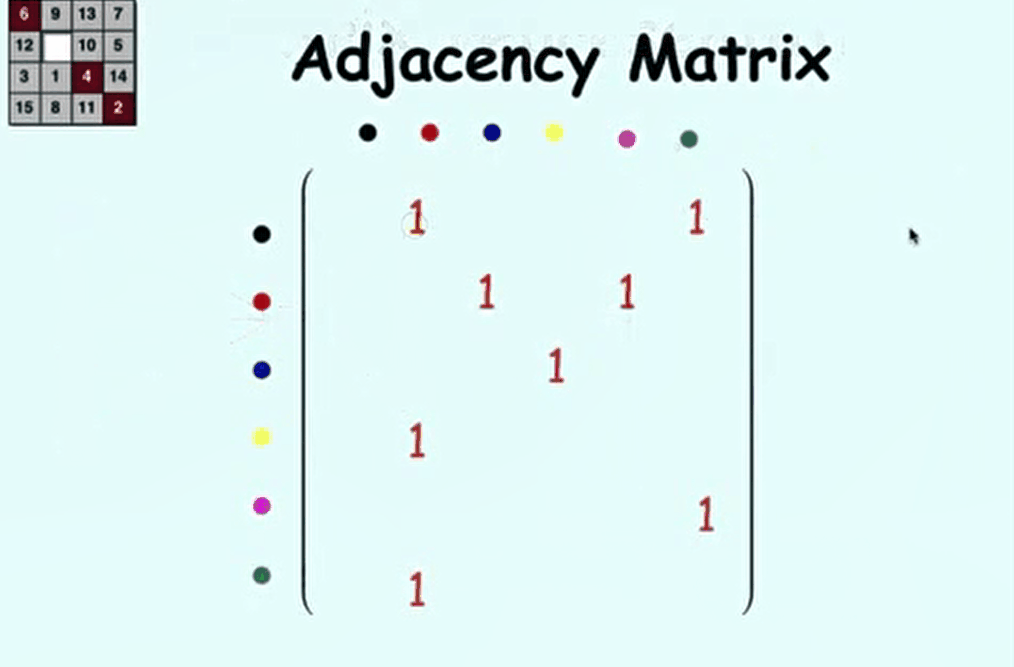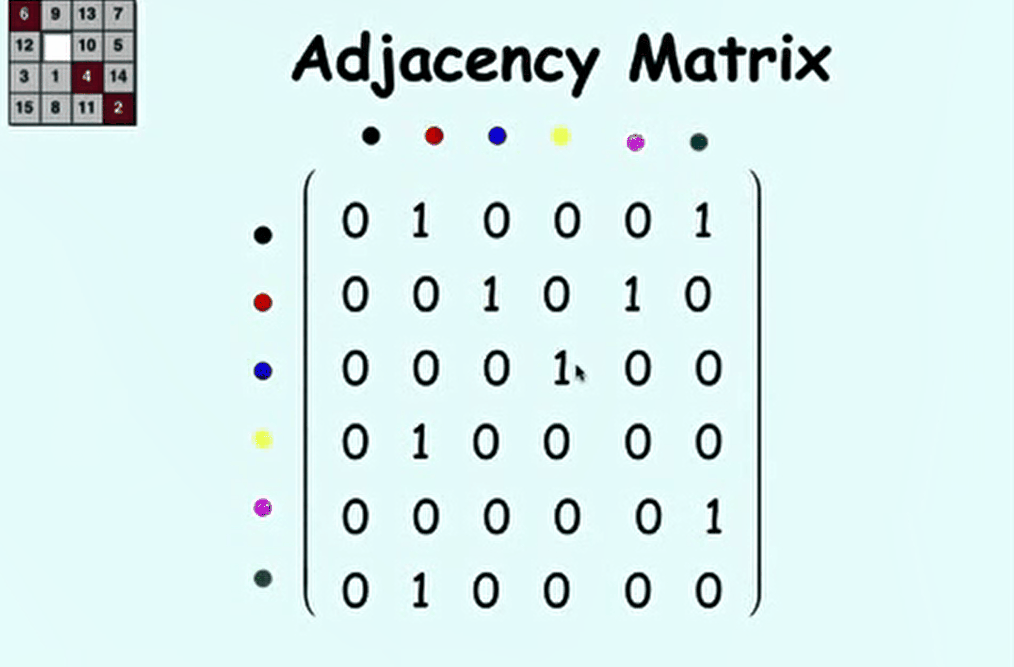
ShowMeAI 对课程资料进行了梳理，整理成这份完备且清晰的资料包：

• 📚 课件：4个单元，111份，覆盖所有课程视频
• 📚 作业练习：12份作业，学后练手的好素材
• 📚 课内问题总结：35份文档，152个常见学习问题与解答
• 📚 拓展阅读材料：35份文档，覆盖所有chapter

课程视频 | B站

【双语字幕+资料下载】MIT 6.042J | 计算机科学的数学基础(2015·完整版)

🌍 B站 | 【双语字幕+资料下载】MIT 6.042J | 计算机科学的数学基础(2015·完整版)

ShowMeAI 将视频上传至B站，并增加了中英双语字幕，以提供更加友好的学习体验。点击页面视频，可以进行预览。推荐前往 👆 B站 观看完整课程视频哦！

全球名校AI课程合辑

• 🚧 CS数学基础课程合辑：https://www.showmeai.tech/tutorials/38
• 🚧 计算机基础课程合辑：https://www.showmeai.tech/tutorials/29
• 🚧 机器学习课程合辑：https://www.showmeai.tech/tutorials/28
• 🚧 深度学习课程合辑：https://www.showmeai.tech/tutorials/77
• 🚧 自然语言处理课程合辑：https://www.showmeai.tech/tutorials/55
• 🚧 计算机视觉课程合辑：https://www.showmeai.tech/tutorials/73
• 🚧 强化学习课程合辑：https://www.showmeai.tech/tutorials/87
• 🚧 AI生物医疗课程合辑：https://www.showmeai.tech/tutorials/74
• 🚧 其他名校AI课程合辑：https://www.showmeai.tech/tutorials/76

作者：ShowMeAI内容团队
阅读原文：https://www.showmeai.tech/article-detail/354