求最短路径 —— 弗洛伊德算法

最新推荐文章于 2025-03-15 15:36:47 发布

Shishishi888

最新推荐文章于 2025-03-15 15:36:47 发布

阅读量4.1k

点赞数 4

分类专栏：数据结构与算法文章标签：最短路径弗洛伊德算法

本文链接：https://blog.youkuaiyun.com/Shishishi888/article/details/98535467

版权

数据结构与算法专栏收录该内容

5 篇文章

订阅专栏

弗洛伊德算法是求图中任意一对顶点间的最短路径的算法。

算法思想

递推产生一个n解方阵序列 $A^{(-1)}$ ， $A^{(0)}$ ，. . . ， $A^{(k)}$ ，. . . ， $A^{(n-1)}$

其中 $A^{(k)}$ [ i ][ j ]表示从顶点 $v_{i}$ 到顶点 $v_{j}$ 的路径长度，k表示绕行第k个顶点的运算步骤。初始时，对于任意两个顶点 $v_{i}$ 和 $v_{j}$ ，若他们之间存在边，则以此边的权值作为它们之间的最短路径长度；若它们之间不存在有向边，则以∞作为它们之间的最短路径长度。以后逐步尝试在原路径中加入顶点k（k=0, 1, . . . , n-1）作为中间顶点。如果增加中间顶点后，得到的路径比原来的路径长度减少了，则以此新路径代替原来的路径。

算法过程

下面用一个例子来说明弗洛伊德算法。

假设有一个图如图所示：

用邻接矩阵储存该图：

弗洛伊德算法需要维护两个矩阵A和Path。矩阵A用来记录当前任意两个顶点的最短路径长度；矩阵Path用来记录当前两个顶点间最短路径上要经过的中间顶点。

为了表述方便，这里把图中的A，B，C，D分别替换为0，1，2，3，算法过程如下。

初始状态：

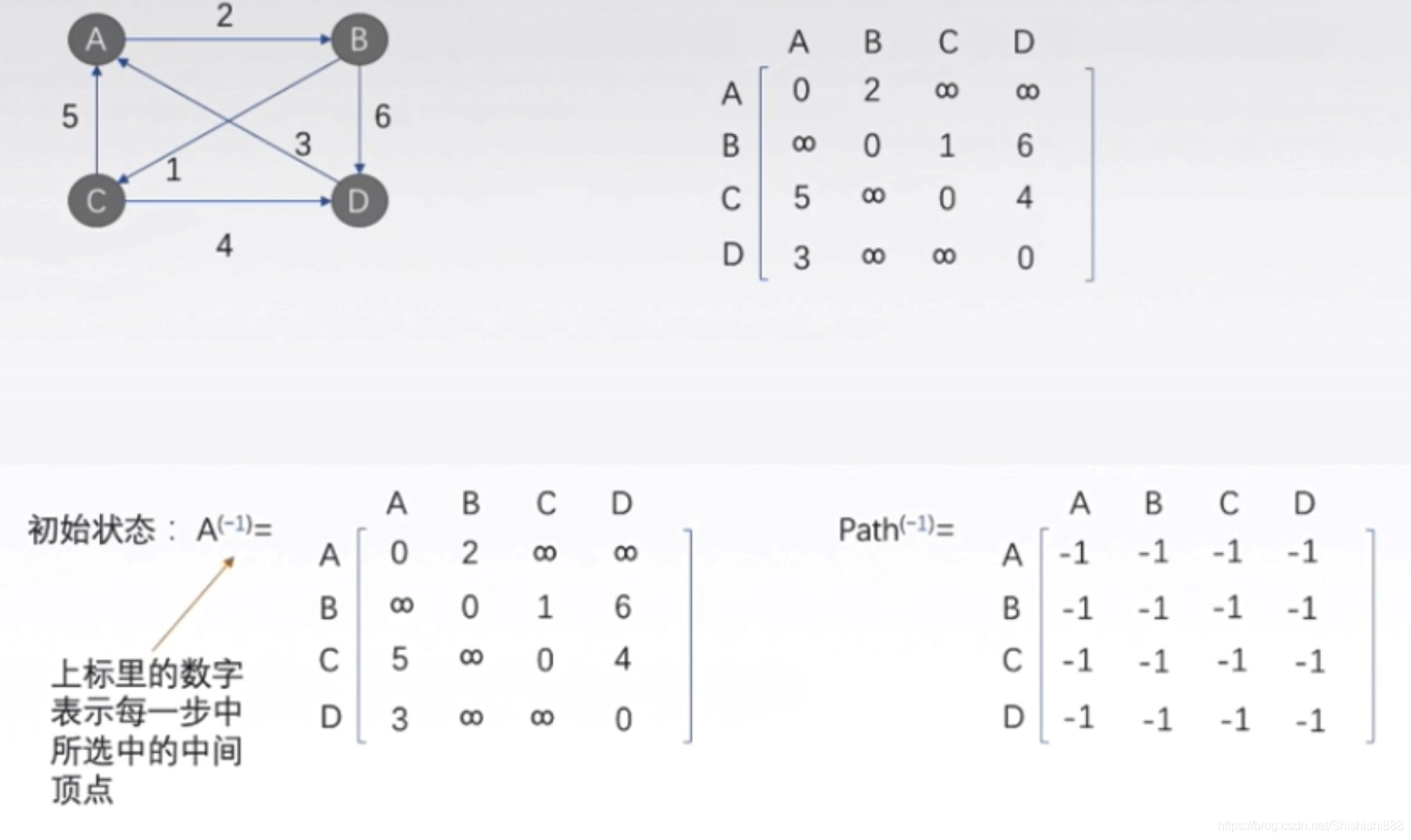
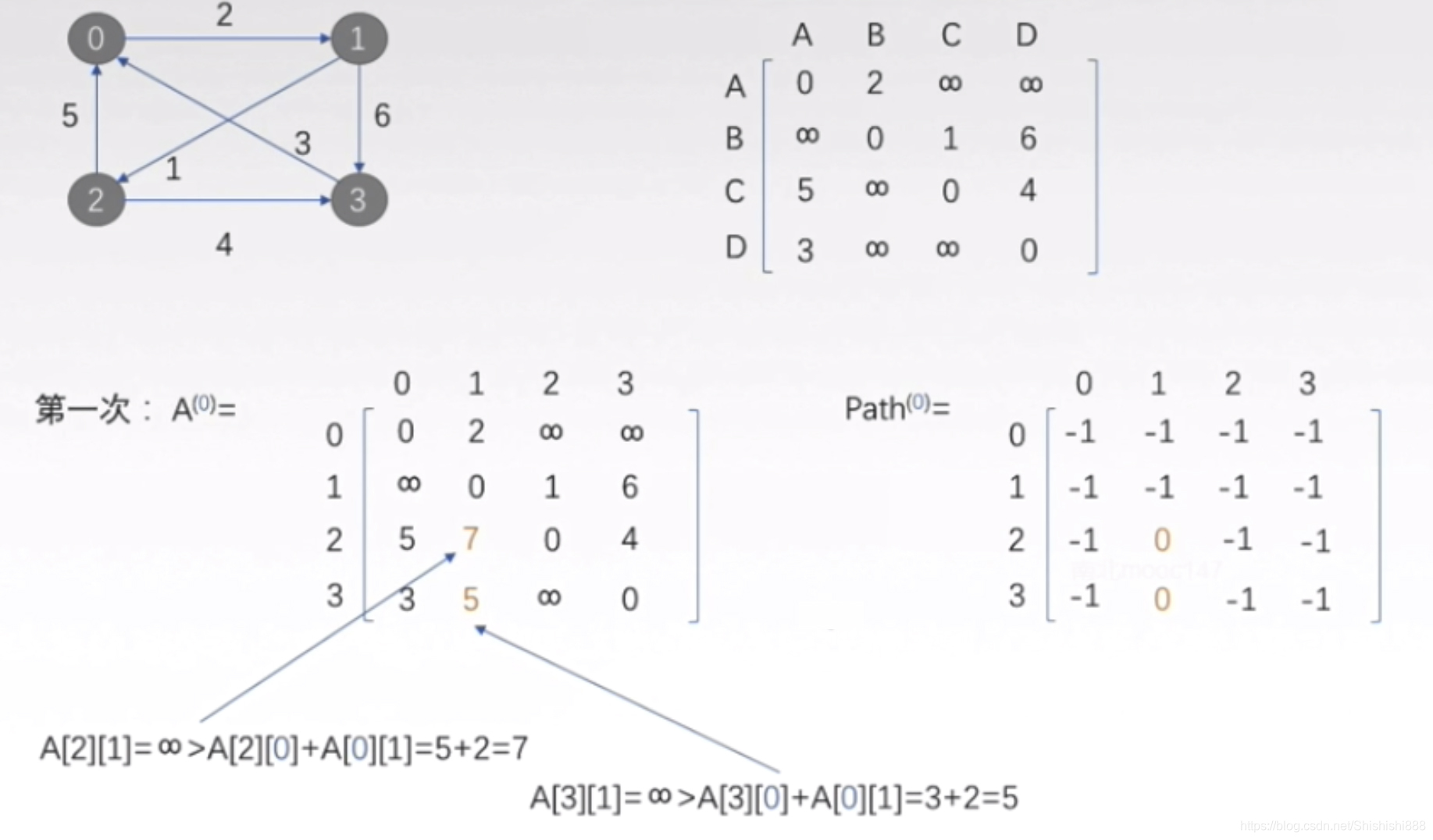
第一轮，选择中间顶点0，比较顶点i，j经过顶点0的路径长度( $v_{i}$ , $v_{0}$ , $v_{j}$ )是否比原来的路径长度( $v_{i}$ , $v_{j}$ )更短，是则替换：

第二轮，选择中间顶点1，比较顶点i，j经过顶点1的路径长度( $v_{i}$ , ... , $v_{1}$ )+( $v_{1}$ , ... , $v_{j}$ )否比第一轮得到的顶点i，j之间的最短路径长度( $v_{i}$ , ... , $v_{j}$ )更短，是则替换，其中，( $v_{i}$ , ... , $v_{1}$ )和( $v_{1}$ , ... , $v_{j}$ )分别是顶点 $v_{i}$ 到 $v_{1}$ ，和顶点 $v_{1}$ 到 $v_{j}$ 的最短路径长度，这两个路径已经在上一步中求出：

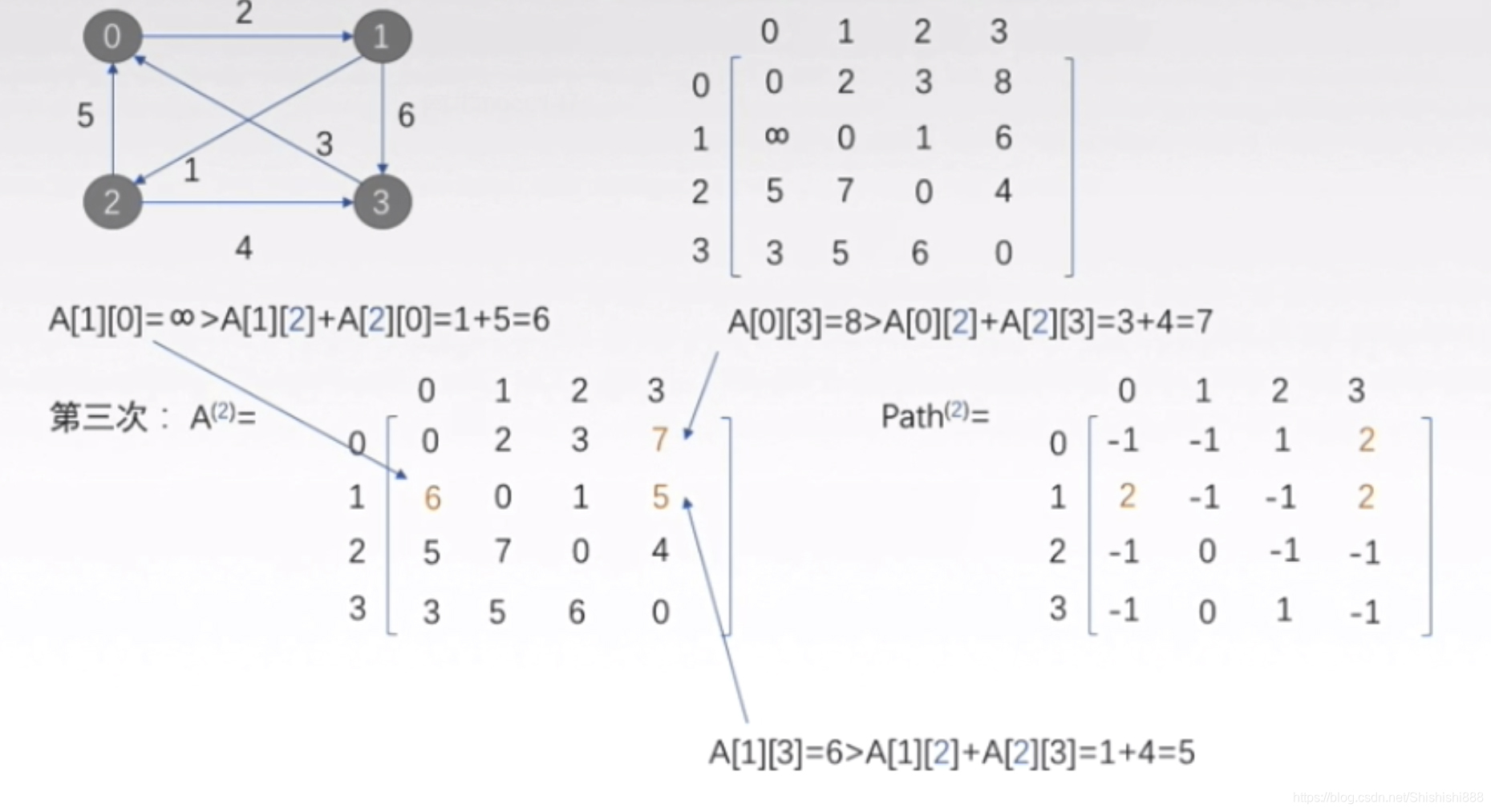
第三轮，选择中间顶点2，比较顶点i，j经过顶点2的路径长度( $v_{i}$ , ... , $v_{2}$ )+( $v_{2}$ , ... , $v_{j}$ )否比第二轮得到的顶点i，j之间的最短路径长度( $v_{i}$ , ... , $v_{j}$ )更短，是则替换，其中，( $v_{i}$ , ... , $v_{2}$ )和( $v_{2}$ , ... , $v_{j}$ )分别是顶点 $v_{i}$ 到 $v_{2}$ ，和顶点 $v_{2}$ 到 $v_{j}$ 的最短路径长度，这两个路径已经在上一步中求出：

第四轮，选择中间顶点3，比较顶点i，j经过结点3的路径长度( $v_{i}$ , ... , $v_{3}$ )+( $v_{3}$ , ... , $v_{j}$ )否比第三轮得到的顶点i，j之间的最短路径长度( $v_{i}$ , ... , $v_{j}$ )更短，是则替换，其中，( $v_{i}$ , ... , $v_{3}$ )和( $v_{3}$ , ... , $v_{j}$ )分别是顶点 $v_{i}$ 到 $v_{3}$ ，和顶点 $v_{3}$ 到 $v_{j}$ 的最短路径长度，这两个路径已经在上一步中求出：

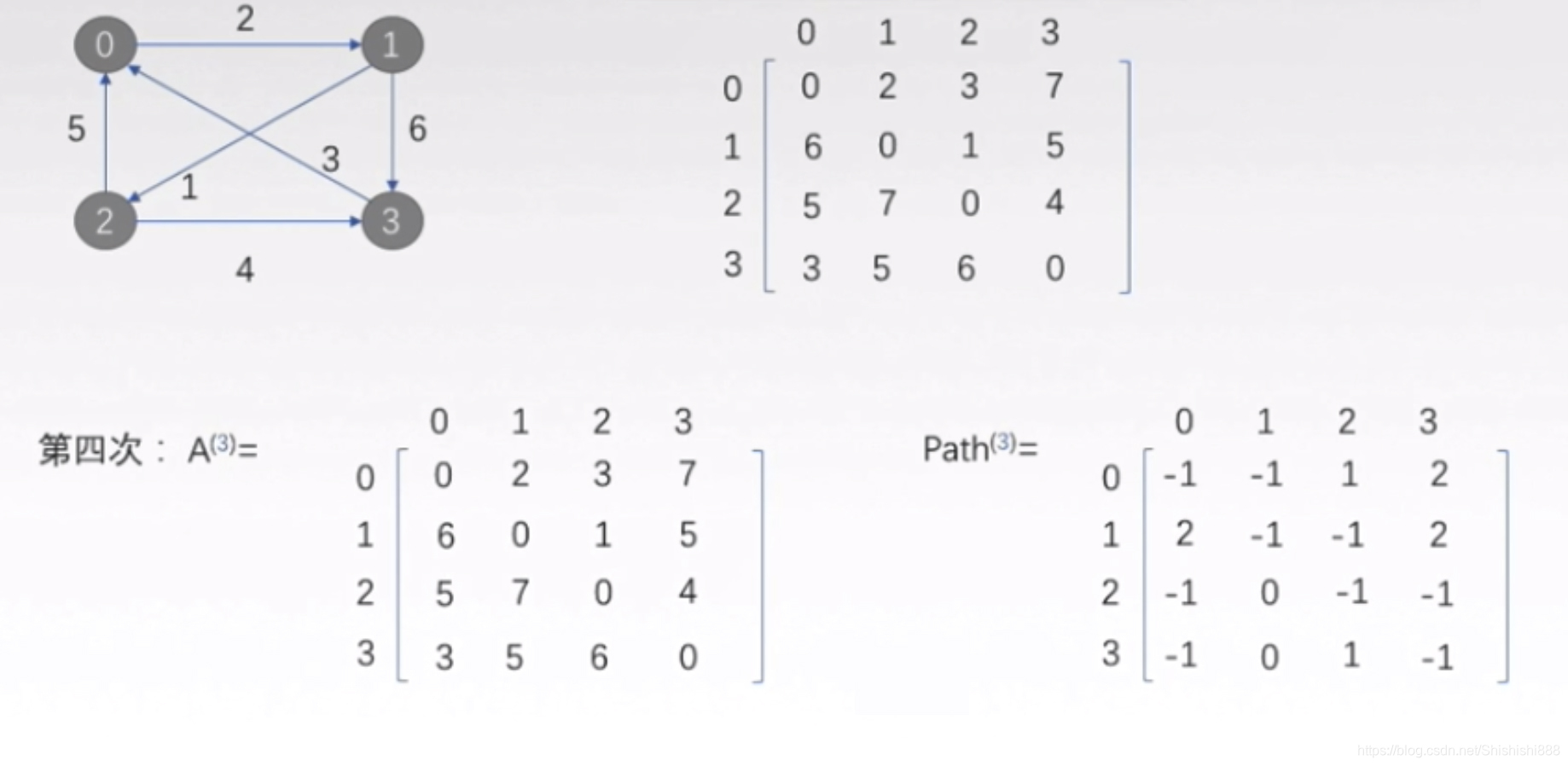
第四轮发现矩阵A和矩阵Path没有任何更新，至此，图中任意两个顶点之间的最短路径长度已经全部求出，弗洛伊德算法执行完毕。

实现代码：

void Floyd(MGraph G, int Path[][]) {
    int i, j, k;
    int A[MAXSIZE][MAXSIZE];
    //对数组A[][]和Path[][]进行初始化
    for(i=0; i<G.vexnums; i++) {
        for(j=0; j<G.vexnums; j++) {
            A[i][j]=G.Edges[i][j];
            Path[i][j]=-1;
        }
    }

    for(k=0; k<G.vexnums; k++) {
        for(i=0; i<G.vexnums; i++) {
            for(j=0; j<G.vexnums; j++) {
                if(A[i][j]>A[i][k]+A[k][j]) {
                    //如果顶点i到顶点j的距离比顶点i经过顶点k到顶点k的距离长，则更新从顶点i到顶点j 
                    //的距离为较小值，并且储存k表示路径经过顶点k   
                   A[i][j]=A[i][k]+A[k][j]
                   Path[i][j]=-1;
                }
            }
        }
    }
}

弗洛伊德算法的核心是一个三重循环，所以时间复杂度是一个O( $n^{3}$ )，其中难过n是图中顶点的个数。