机器学习基础：理解机器学习算法

什么是机器学习

人类学习就是从经验中获得知识和技能，人们通过阅读、沟通、听讲、研究、实践获取经验，然后再对经验进行梳理、分析和研究，最后形成知识和技能。

机器学习类似于人类学习，它也需要从外部获得经验，这里的经验是指输入到程序的经验数据，程序通过学习算法分析经验数据并从中学习，学习结果会形成一个模型（模型可以理解为程序从经验数据学到的知识和技能），程序使用该模型完成设定的工作，如预测和控制两个变量间的相互变化、机器翻译、语音识别等工作。

对于初次接触机器学习的读者来说，它还是一个比较深奥、抽象化的概念。虽然概念很抽象，不过人们每天都或多或少与机器学习系统（把机器学习定义为系统会更好一些，因为它是由若干部分构成的）打过交道。

例如：刷脸支付就是一个机器学习系统，它会记住人脸表情的每一次变化，防止识别错误或使用照片来模拟人脸，人脸检测是机器学习视觉领域被深入研究的一个问题。

再如：人们经常使用的翻译工具（如百度翻译、谷歌翻译等）也是一个机器学习系统，它学习的数据是语料库（语料库存放的是在语言实际使用中真实出现过的语言材料），生成翻译统计模型，由模型完成句子的翻译。

卡内基梅隆大学教授Tom Mitchell在他所著的《机器学习》一书里为机器学习给出了一个简洁的定义：“对于某类任务T和性能度量P，一个计算机程序被认为可以从经验E中学习是指，通过经验E改进后，它在任务T上由性能度量P衡量的性能有所提升”。

任务T可以理解为机器学习程序要实现的目标，如通过身高预测体重是程序要实现的目标、把中文自动翻译成英文是程序要实现的目标等待。

程序要实现任务T的目标，需要从经验E中学习，学习过程不能算是任务，学习是程序获取完成任务的能力，即建立与任务目标适配的模型。对于通过身高预测体重任务来说，建立回归预测模型；对于自动翻译任务来说，建立翻译统计模型。

经验E为已经量化的与任务相关的特征数据，如数据集train_hw.csv存储了经过测量的身高和体重，身高和体重就是特征数据，身高和体重都已经标量化（纯数值）。程序处理这些数据时，会将这些数据表示成一个向量，向量的每个分量是一个特征数据。

为了度量模型的性能，还需要设计性能度量P，用来评估模型工作的准确性。性能度量P也是一个程序，程序的输入是测试数据集，因为我们更加关注模型在未观测数据上的性能如何，因为这将决定机器学习程序在实际应用中的性能。

下面我们通过一个简单机器学习的案例，来理解机器学习的过程。

任务目标

案例任务T目标是是建立一个预测模型，该模型可以根据人的身高来预测人的体重，若人的身高和体重是线性关系，该模型将会正确地工作，当然一些特例数据可能会让模型预测失误。

数据准备

编写机器学习程序的第一步是要搜集和整理用于建立预测模型的经验数据，现在我们手上有数据集SOCR-HeightWeight.csv（数据集仅限于学习使用），该数据集记录了25,000个18岁不同人的身高（英寸）和体重（磅），利用这个数据集，可以建立身高—体重预测模型。

下表列出了该数据集的内容：

经验E的数据在程序中一般使用向量来表示，使用Numpy的数组可以表示向量。

例如：

>>>importnumpyasnp>>> v = np.array%28[65.78331,112.9925]%29

上面的代码创建了向量v，v存储了上表的第1条记录（数据集的第1个样本，Index字段除外）。若要存储全部样本数据，可以使用Numpy二维数组来存储样本数据。

例如：

importnumpyasnpM = np.array%28[ [65.78331,112.9925], [71.51521,136.4873], …… [70.84235,142.4235] ]%29

上面的代码创建了矩阵M，M是n X 2的矩阵，M的每一行是一个样本，M的每一列对应数据集的不同特征，如第1列是身高，第2列是体重。

数据集规模比较大，简单起见，我们抽取两个子集：一个子集作为经验数据（即训练数据）；一个子集作为为测试数据。经验数据用于模型的建立和调试，测试数据验证模型的正确性。

训练数据子集为：train_hw.csv

测试数据子集为：test_hw.csv

学习算法设计

有了经验数据E，就要考虑设计学习算法了。学习算法是从经验数据E中找出数据集变量间的函数关系，即建立预测模型（函数模型）。

在该数据集中，有两个变量身高和体重，体重是因变量，身高是自变量，因变量和自变量的函数关系，需要我们通过散点图来确定。可以使用matplotlib绘制经验数据的散点图，观察数据点的分布情况，发现身高和体重两个变量间的因果关系，从而建立预测模型。

例1绘制train_hw.csv数据子集散点图

# 导入numpy库importnumpyasnpimportmatplotlib.pyplotasplt程序入口if__name__ ==%27__main__%27: # 从数据集文件读取1、2列 data= np.genfromtxt%28%27train_hw.csv%27,delimiter=%27,%27,dtype=%27float%27,usecols=[1,2]%29 x =data[::,1] y =data[::,0] fig, ax = plt.subplots%281,1%29 # 绘制散点图 ax.scatter%28x,y, s=20, c=x%29 plt.show%28%29

train_hw.csv数据子集散点图如下图所示：

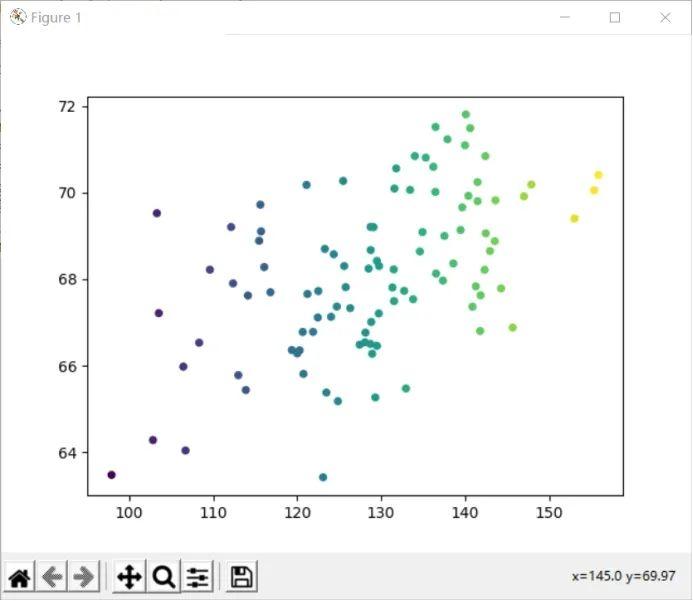
散点图X轴为身高，Y轴为体重。观察散点图发现，身高和体重呈现一定的线性关系，大致的线性关系可以用下面的直线进行拟合：

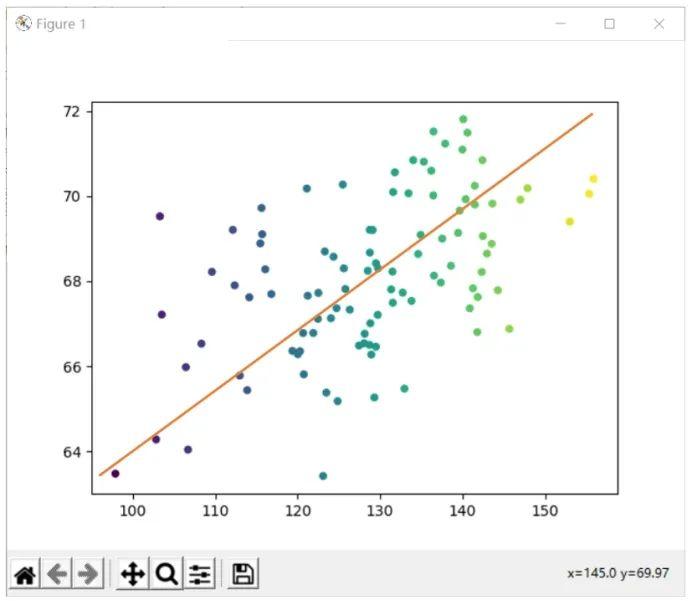
拟合直线方程为：

f%28x%29 = ax + b

其中a和b是待定系数，机器学习的主要工作就是依据给出的经验数据确定a和b的值，从而确定f%28x%29函数，也就是确定预测模型。

这种方法也称为线性回归，目标是建立一个系统，将向量x作为输入,预测标量y作为输出，线性回归的输出是输入的线性函数，令ý表示模型预测y应该取的值，回归输出为：

ý = ax + b

其中ý是模型预测y的结果值，a是参数向量，其分量个数和向量x的分量个数相同，在本案例中a和x仅有一个分量，b是在y轴的截距，若b为0，该直线会通过坐标轴的原点，b也称为偏置参数。

现在问题的关键是如何确定a和b的值，让ý（预测值）最接近y（真实值）。

ý最接近y值，即预测值与真实值的差值最小，也就是预测值与真实值的偏差最小。

我们前面建立的测试数据子集就是用来度量预测模型的性能，度量方法是计算预测模型在测试数据集上的偏差。如果用ý%28test%29表示预测模型在测试集上的预测值，那么总偏差表示为：

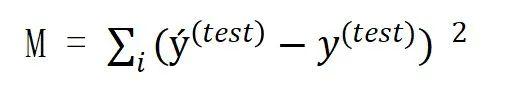
其中M是预测值与真实值的总偏差，ý%28test%29是预测值，y%28test%29是真实值。

编写机器学习程序的第三步就是构建一个机器学习算法，通过学习训练集获得经验，减少M以改进系数a和b，最小化训练集上的总偏差M。

这种根据总偏差作为最小的条件来选择系数a、b的方法叫做最小二乘法，是线性回归经常采用的方法。

下面的问题是如何改进a和b的值，可以使M取得最小值。将预测模型代入总偏差公式：

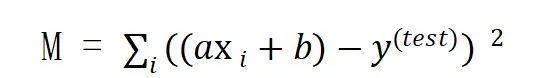
在上面的公式中，我们希望使所有偏差的平方和最小，如何求最小值M呢？可以通过微积分的方法得到，把偏差的平方和看作函数，它有a和b两个变量，求这个函数的最小值。

该函数是二元二次函数，分别求变量a和b的偏导函数，令偏导数为0，M取得最小值。下面的Python程序求变量a和b的偏导函数。

例2求变量a和b的偏导函数

fromsympy import difffromsympy import symbolsimport numpy as np# 定义计算偏导的函数def func%28data,a,b%29: exp ="" for i,item inenumerate%28data%29: exp +="%28"+str%28item[0]%29 +"-"+"%28"+str%28item[1]%29 +"%2Aa+b%29%29 %2A%2A 2" if i %21=len%28data%29 -1: exp +="+" returneval%28exp%29# 程序入口if __name__ ==%27__main__%27: # 从训练数据集读取数据 data = np.genfromtxt%28%27train_hw.csv%27,delimiter=%27,%27,dtype=%27float%27,usecols=[1,2]%29 a =symbols%28"a"%29 b =symbols%28"b"%29 # 计算变量a的偏导函数 print%28diff%28func%28data,a,b%29,a%29%29 # 计算变量b的偏导函数 print%28diff%28func%28data,a,b%29,b%29%29

程序执行后，得到下面的方程组：

3368087.42631065%2Aa+25841.82342%2Ab-1763213.6453413525841.82342%2Aa+200.0%2Ab-13628.21132

求解上面的方程组，即可求得a和b的值，确定回归输出的预测模型。我们使用Python的NumPy库来求解上面的方程组。

例3求解方程组

# 导入numpy库importnumpyasnp# 程序入口if__name__ ==%27__main__%27: # 建立2X2矩阵 ta = np.array%28[[3368087.42631065,25841.82342],[25841.82342,200.0]]%29 # 建立2维向量 tb = np.array%28[1763213.64534135,13628.21132]%29 # 解线性方程组 x = np.linalg.solve%28ta,tb%29 # 输出x和y的值 print%28"a = %.2f b = %.2f"% %28x[0],x[1]%29%29

运行上面的Python程序，求得:

a = 0.08, b = 57.82

回归输出预测模型为：

ý = 0.08x + 57.8

模型性能度量

对模型的性能度量，主要采用绘图直观比较和均方误差进行。可以先直观上了解一下预测模型是否合适，使用matplotlib绘制训练数据和测试数据的散点图，同时绘制预测模型的直线方程。

例4绘制预测模型效果图

# 导入numpy库importnumpyasnpimportmatplotlib.pyplotasplt# 定义绘图函数def plotter%28ax, data1, data2, param_dict,type%29: iftype ==0: ax.scatter%28x,y,%2A%2Aparam_dict%29 else: ax.plot%28data1, data2, %2A%2Aparam_dict%29# 获取预测模型直线方程数据def get_line_data%28x%29: y =0.08%2A x +57.82 return%28x,y%29# 程序入口if__name__ ==%27__main__%27: # 读取训练数据集 data= np.genfromtxt%28%27train_hw.csv%27,delimiter=%27,%27,dtype=%27float%27,usecols=[1,2]%29 x =data[::,1] y =data[::,0] fig, ax = plt.subplots%281,1%29 # 设置图例中文显示 plt.rcParams[%27font.sans-serif%27] = [%27SimHei%27] # 绘制训练数据 plotter%28ax,x,y,{%27color%27:%27b%27,%27label%27:%27训练集%27},0%29 # 获取预测模型直线方程数据 x1,y1 = get_line_data%28x%29 plotter%28ax,x1,y1,{%27color%27:%27m%27,%27label%27:%27预测模型直线方程%27},1%29 # 读取测试数据集 data= np.genfromtxt%28%27test_hw.csv%27,delimiter=%27,%27,dtype=%27float%27,usecols=[1,2]%29 x =data[::,1] y =data[::,0] # 绘制测试数据 plotter%28ax,x,y,{%27color%27:%27r%27,%27label%27:%27测试集%27},0%29 # 显示图例 plt.legend%28%29 plt.show%28%29

预测效果图如下：

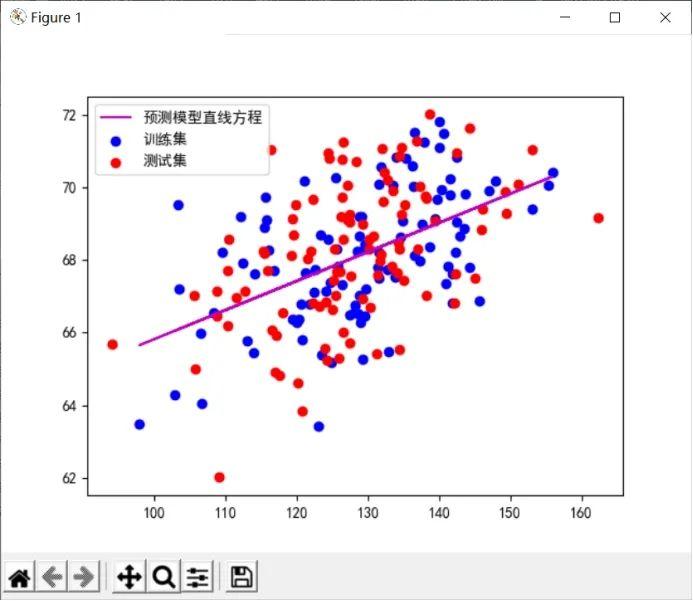
从上图可以看出，预测模型的直线较好拟合了测试集合数据集。

度量回归预测模型的性能最常用的方法是计算预测值与真实值的均方误差（MSE），均方误差（MSE）的计算方法为总偏差除以样本个数，计算公式为：

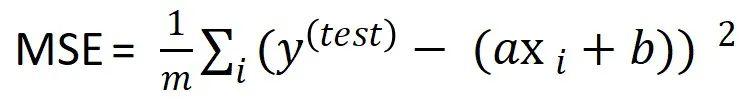
例5计算均方误差（MSE）

# 导入numpy库importnumpyasnpimportmatplotlib.pyplotasplt# 定义计算MSE的函数def calculation_mse%28data,a,b,m%29: exp ="" fori,iteminenumerate%28data%29: exp +="%28"+ str%28item[0]%29 +"-"+"%28"+ str%28item[1]%29 +"%2Aa+b%29%29 %2A%2A 2" ifi %21= len%28data%29 -1: exp +="+" mse = eval%28exp%29 / m returnmse# 定义绘图函数def plotter%28ax, data1, data2, param_dict,type%29: iftype ==0: ax.scatter%28data1,data2,%2A%2Aparam_dict%29 else: ax.plot%28data1, data2, %2A%2Aparam_dict%29# 获取预测模型直线方程数据def get_line_data%28x%29: y =0.08%2A x +57.82 return%28x,y%29# 程序入口if__name__ ==%27__main__%27: # 读取测试数据集 data= np.genfromtxt%28%27test_hw.csv%27,delimiter=%27,%27,dtype=%27float%27,usecols=[1,2]%29 # 区间[0.01,0.2]创建50个数据点 x = np.linspace%280.01,0.2,50%29 y = [] # 对每个x取值计算MSE forx1inx: mse = calculation_mse%28data,x1,57.82,len%28data%29%29 y.append%28mse%29 fig, ax = plt.subplots%281,1%29 plotter%28ax,x,y,{%27color%27:%27m%27,%27label%27:%27MSE%27},1%29 # 计算x取值0.08的MSE a_mse = calculation_mse%28data,0.08,57.82,len%28data%29%29 plotter%28ax,0.08,a_mse,{%27color%27:%27b%27},0%29 plt.text%280.08,a_mse,%280.08,a_mse%29,color=%27r%27%29 plt.grid%28True%29 # 显示图例 plt.legend%28%29 plt.show%28%29

计算结果如下图所示：

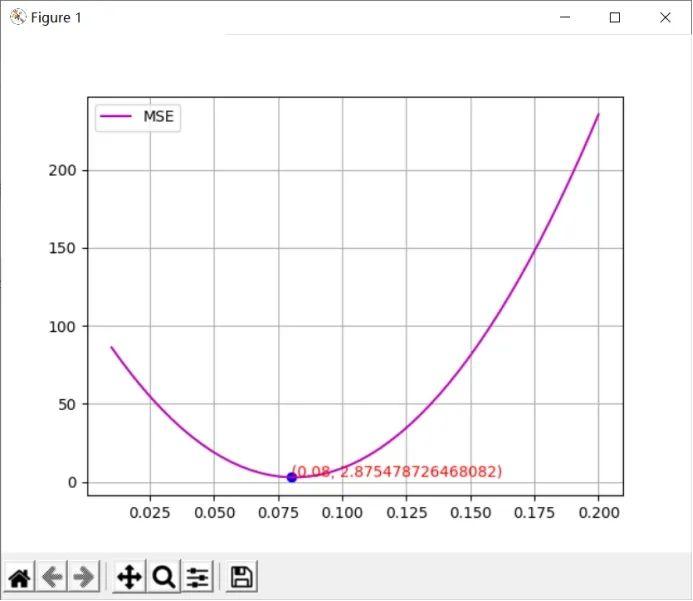
上图是预测模型系数a在区间[0.01,0.2]的MSE曲线，从图中可以看出系数a在0.08处取得MSE最小值，均方误差（MSE）约为2.87，说明预测模型与测试数据集有较好的拟合度。