2024软工K班结对编程任务

原创 已于 2025-11-21 12:33:18 修改 · 950 阅读 · 10 ·
CC 4.0 BY-SA版权
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
文章标签：

#结对编程

于 2025-11-20 21:14:29 首次发布

https://github.com/ShaddockNH3/FZU-SE-Neko-Caller

https://blog.youkuaiyun.com/Shaddock42125/article/details/155076245?sharetype=blogdetail&sharerId=155076245&sharerefer=PC&sharesource=Shaddock42125&spm=1011.2480.3001.8118

https://live.youkuaiyun.com/v/501761

一、结对探索

1.1 队伍基本信息

结对编号：01；队伍名称：NekoCaller；

学号姓名具体分工
022302217郑伟负责设计数据库，实现基本的全盘逻辑，增加趣味功能
052306116周晨烁实现前端以及实现了导入表格等逻辑

1.2 描述结对的过程

在本次结对编程任务中，我们两人通过线上协作的方式完成了课堂随机点名系统的开发。郑伟负责后端数据库设计和核心业务逻辑的实现，周晨烁负责前端界面开发和数据导入功能。我们通过GitHub进行代码版本管理，使用 Issues 和 Pull Requests 进行任务分配和代码审查。初期通过 QQ 讨论需求分析和原型设计，后续通过代码提交和合并保持同步。

1.3 非摆拍的两人在讨论设计或结对编程过程的照片

在这里插入图片描述

二、原型设计

2.1 原型工具的选择

我们选择了墨刀作为原型设计工具，因为它支持实时协作、丰富的交互设计功能，且免费版足以满足我们的需求。墨刀的组件库和模板功能帮助我们快速搭建界面原型。

2.2 遇到的困难与解决办法

在原型设计过程中，我们遇到的主要困难是：

  1. 如何设计趣味性事件系统的交互界面
  2. 点名结算流程的逻辑梳理

通过多次讨论和参考优秀作业，我们采用了标签展示事件效果、滑块控制分数的方式解决。

2.3 原型作品链接

https://modao.ink/proto/VzUtCFsXt60z386qdyGpdp/sharing?view_mode=read_only&screen=rbpV35rGLl8tbNXnG

2.4 原型界面图片展示

主页面

  • 显示班级列表和统计信息
  • 快速操作入口：导入数据、开始点名、查看排行榜

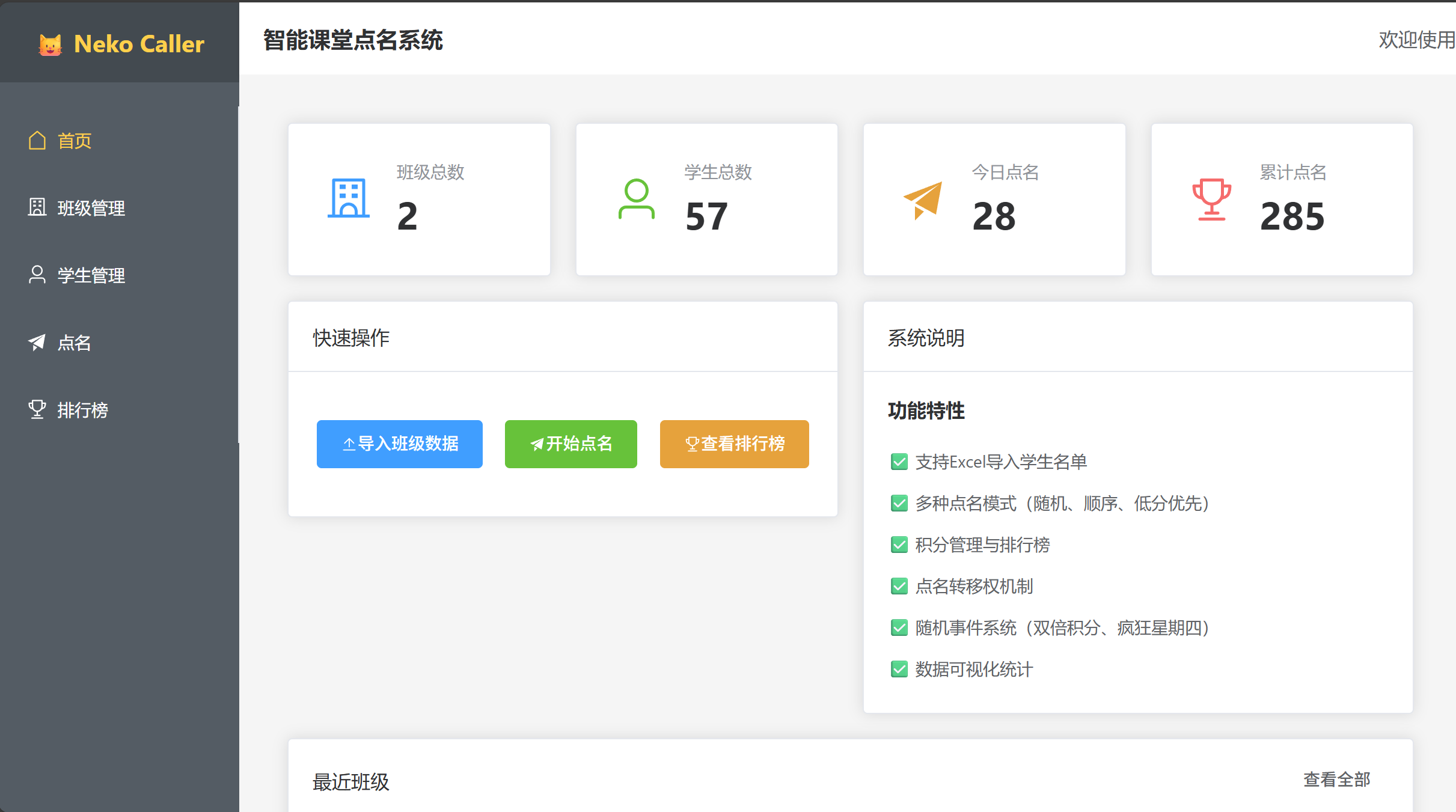
在这里插入图片描述

点名界面

  • 左侧配置区：选择班级、点名模式、事件类型
  • 右侧结果区：显示被点名学生信息和结算表单
  • 支持多种事件：双倍积分、疯狂星期四、1024福报等

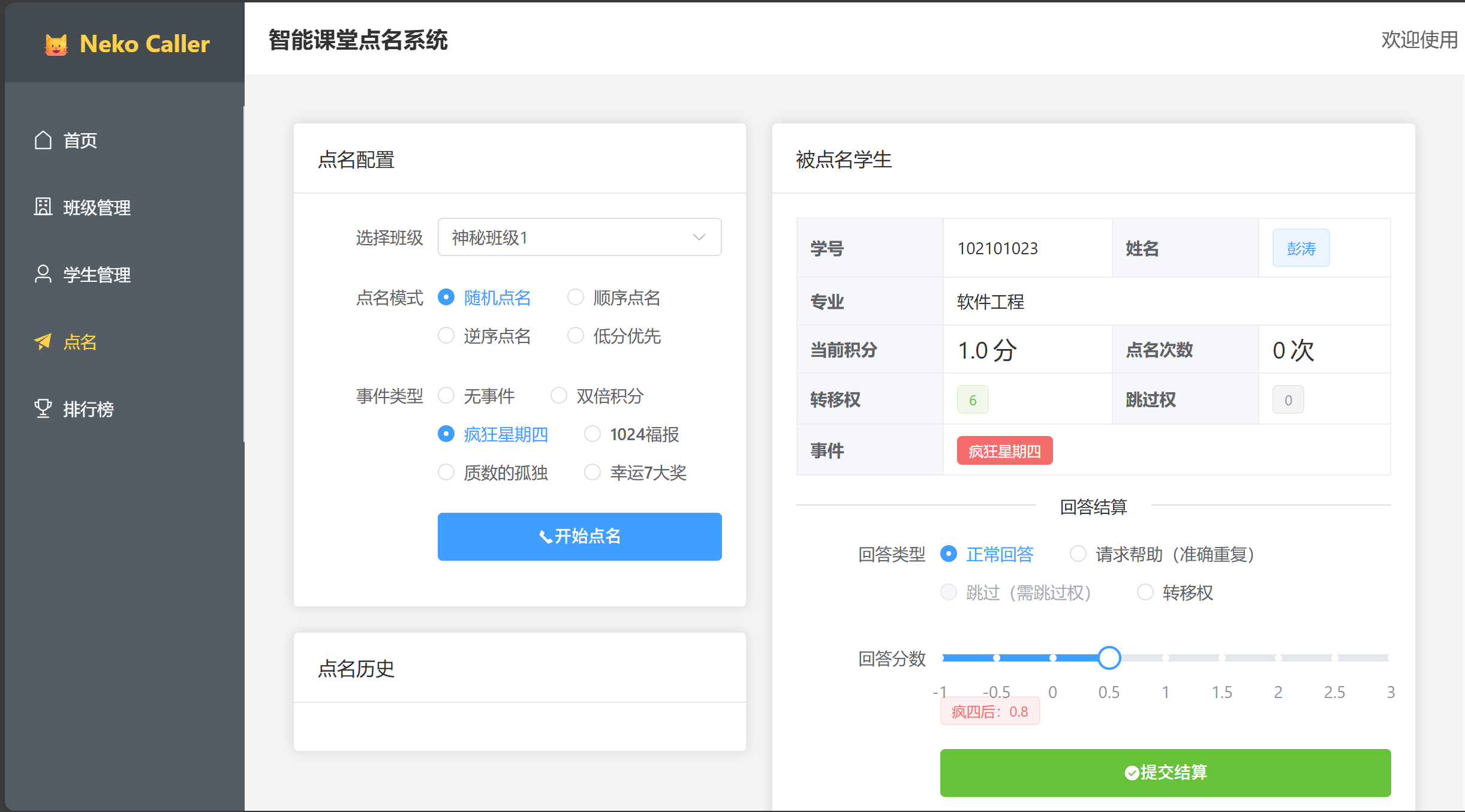
在这里插入图片描述

排行榜界面

  • 展示Top N学生排名
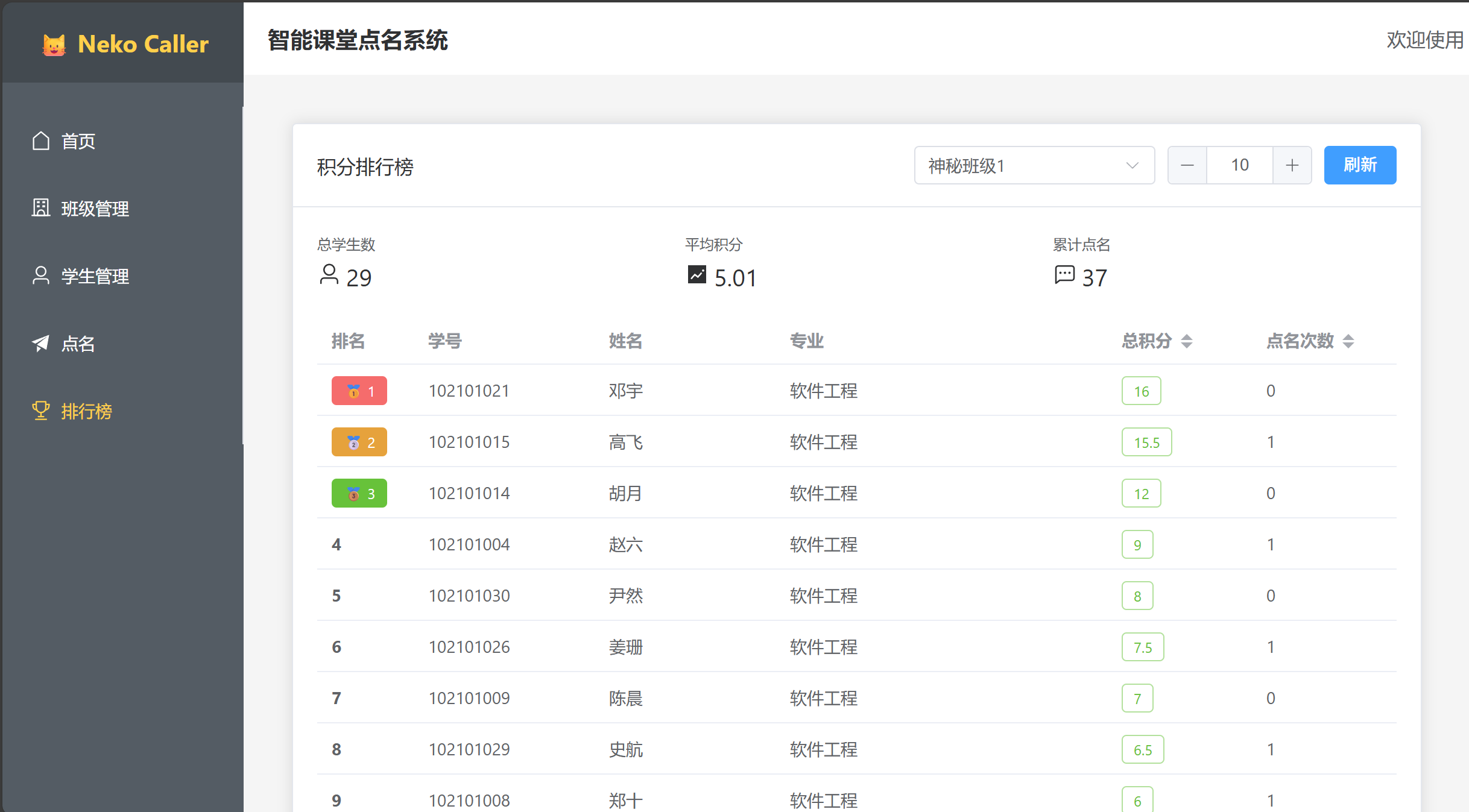
    在这里插入图片描述

三、编程实现

3.1 开发工具库的使用

后端使用了：

  • Hertz：高性能HTTP框架，由CloudWeGo提供，支持高并发请求处理
  • GORM：ORM框架，用于数据库操作，支持多种数据库
  • gorm-gen：GORM代码生成工具，自动生成数据库查询代码，提高开发效率
  • Excelize：Excel文件处理库，用于导入导出学生名单和积分详单
  • Thrift：RPC框架，用于定义API接口和数据结构
  • UUID：唯一标识符生成库，用于生成班级ID、选课ID等主键

前端使用了：

  • Vue 3：渐进式JavaScript框架，支持组合式API
  • Element Plus：Vue 3 UI组件库，提供丰富的界面组件
  • Axios：HTTP客户端，用于与后端API通信
  • Vue Router 4：官方路由管理器，支持单页应用导航

数据库使用了：

  • MySQL 8：关系型数据库，部署在db4free.net免费托管服务上

3.2 代码组织与内部实现设计

类图设计

数据模型类

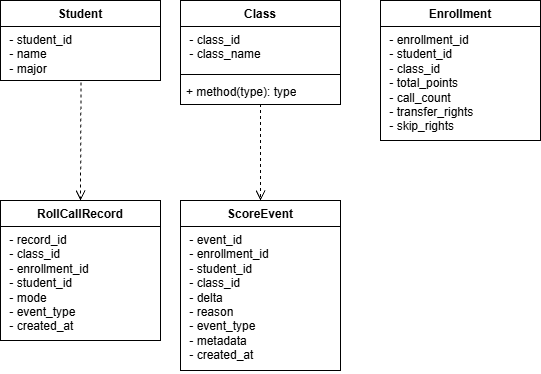
在这里插入图片描述

服务类关系

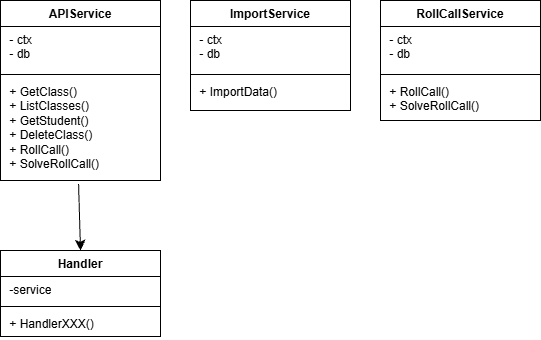
在这里插入图片描述

项目目录结构

FZU-SE-Neko-Caller/
├── docs/                          # 文档目录
│   ├── 0.作业要求文档.md          # 作业要求
│   ├── API文档.md                 # API文档
│   ├── architecture.md            # 架构文档
├── NekoCallerBackend/             # 后端代码
│   ├── main.go                    # 程序入口
│   ├── go.mod                     # Go模块文件
│   ├── biz/                       # 业务逻辑层
│   │   ├── dal/                   # 数据访问层
│   │   │   ├── model/             # 数据模型
│   │   │   ├── mysql/             # 数据库连接
│   │   │   └── query/             # GORM生成查询
│   │   ├── handler/               # HTTP处理器
│   │   ├── service/               # 业务服务层
│   │   └── router/                # 路由注册
│   ├── idl/                       # Thrift IDL定义
│   └── pkg/                       # 公共包
│       ├── constants/             # 常量定义
│       ├── errno/                 # 错误码
│       └── utils/                 # 工具函数
└── NekoCallerFrountend/           # 前端代码
    ├── index.html                 # HTML入口
    ├── package.json               # Node.js依赖
    ├── vite.config.js             # Vite配置
    ├── public/                    # 静态资源
    └── src/                       # 源代码
        ├── main.js                # Vue入口
        ├── App.vue                # 根组件
        ├── api/                   # API接口
        ├── router/                # 路由配置
        └── views/                 # 页面组件

3.3 算法关键与流程图

核心算法说明

本系统的核心算法包括四种点名模式:加权随机点名、顺序点名、逆序点名以及低分优先点名。其中加权随机点名和低分优先点名是两个核心算法。

1. 加权随机算法实现

加权随机点名通过积分和点名次数计算权重,确保积分较低的学生被点到的概率更高,同时支持多种趣味事件来调整权重。

权重计算公式:

weight=11+points×0.4+callCount×0.2 weight = \frac{1}{1 + points \times 0.4 + callCount \times 0.2} weight=1+points×0.4+callCount×0.21​

其中:

  • points: 学生当前总积分
  • callCount: 学生被点名次数
  • 系数0.4和0.2分别控制积分和点名次数对权重的影响

特点:

  • 积分越低,权重越高,被点到的概率越大
  • 点名次数越多,权重越低,确保公平性
  • 支持多种随机事件加成(双倍积分、疯狂星期四等)
func randomRoll(roster []*common.RosterItem, event common.RandomEventType) (common.RosterItem, error) {
    weights := make([]float64, len(roster))
    total := 0.0
    
    // 计算每个学生的权重
    for i, item := range roster {
        w := baseWeight(item)
        
        // 事件权重调整
        switch event {
        case common.RandomEventType_Double_Point:
            w *= 1.3
        case common.RandomEventType_CRAZY_THURSDAY:
            // 积分为50的因数时权重增加
            if isFactorOf50(item.EnrollmentInfo.TotalPoints) {
                w *= 1.25
            }
        }
        
        weights[i] = w
        total += w
    }
    
    // 使用累积分布随机选择
    randPoint := rng.Float64() * total
    for i, weight := range weights {
        if randPoint <= weight {
            return *roster[i], nil
        }
        randPoint -= weight
    }
    
    return *roster[len(roster)-1], nil
}

func baseWeight(item *common.RosterItem) float64 {
    points := math.Max(item.EnrollmentInfo.TotalPoints, 0)
    callCount := math.Max(float64(item.EnrollmentInfo.CallCount), 0)
    return 1 / (1 + points*0.4 + callCount*0.2)
}

2. 低分优先算法实现

低分优先点名采用分段正态分布策略,将学生按积分和点名次数排序后,从积分最低的前1/3学生中随机选择一个进行点名。这种算法确保了积分较低的学生有更高的被点概率,同时保持一定的随机性。

算法步骤:

  1. 按照积分升序排序(积分相同则按点名次数升序)
  2. 选取前 ⌈n/3⌉ 名学生(n为总学生数)
  3. 从这些学生中随机选择一个

数学模型:

candidates=⌈n3⌉ candidates = \left\lceil \frac{n}{3} \right\rceil candidates=⌈3n​⌉

selected=random(sorted_roster[0:candidates]) selected = random(sorted\_roster[0:candidates]) selected=random(sorted_roster[0:candidates])

特点:

  • 积分最低的学生群体有100%被候选的概率
  • 保证了对学习困难学生的关注
  • 避免了完全确定性点名带来的可预测性
  • 兼顾公平性和激励性
func lowPointsFirst(roster []*common.RosterItem) common.RosterItem {
    // 复制名册避免修改原数据
    copyRoster := make([]*common.RosterItem, len(roster))
    copy(copyRoster, roster)
    
    // 按积分和点名次数排序
    sort.Slice(copyRoster, func(i, j int) bool {
        if copyRoster[i].EnrollmentInfo.TotalPoints == copyRoster[j].EnrollmentInfo.TotalPoints {
            // 积分相同时,按点名次数升序
            return copyRoster[i].EnrollmentInfo.CallCount < copyRoster[j].EnrollmentInfo.CallCount
        }
        // 按积分升序
        return copyRoster[i].EnrollmentInfo.TotalPoints < copyRoster[j].EnrollmentInfo.TotalPoints
    })
    
    // 计算候选范围: 最多前1/3的学生,至少1个
    limit := int(math.Max(1, math.Ceil(float64(len(copyRoster))/3)))
    
    // 从候选范围内随机选择
    return *copyRoster[rng.Intn(limit)]
}

算法对比分析:

特性加权随机低分优先
公平性★★★★☆★★★★★
随机性★★★★★★★★☆☆
可预测性低中等
激励效果强很强
适用场景常规点名照顾后进生

3. 趣味随机事件系统

为了增加课堂互动的趣味性,系统设计了五种特殊的随机事件,每种事件都有独特的触发条件和积分加成规则:

3.1 双倍积分 (Double Point)

事件说明: 最基础的加成事件,所有积分变化翻倍。

触发条件: 无条件触发

积分规则:

  • 正常回答/请求帮助的积分 × 2
  • 跳过/转移不受影响

实现代码:

case common.RandomEventType_Double_Point:
    if req.AnswerType == common.AnswerType_NORMAL || req.AnswerType == common.AnswerType_HELP {
        base *= 2
    }

3.2 疯狂星期四 (Crazy Thursday)

事件说明: 致敬肯德基疯狂星期四,积分为50的因数的学生有额外权重加成。

触发条件: 无条件触发

积分规则:

  • 正常回答/请求帮助的积分 × 1.5
  • 跳过/转移不受影响

权重加成: 当学生总积分为50的因数(1, 2, 5, 10, 25, 50)时,被点名权重 × 1.25

实现代码:

case common.RandomEventType_CRAZY_THURSDAY:
    // 权重调整
    if isFactorOf50(item.EnrollmentInfo.TotalPoints) {
        w *= 1.25
    }
    // 积分加成
    if req.AnswerType == common.AnswerType_NORMAL || req.AnswerType == common.AnswerType_HELP {
        base *= 1.5
    }

func isFactorOf50(points float64) bool {
    intPoints := int(points)
    if intPoints <= 0 || intPoints > 50 {
        return false
    }
    return 50%intPoints == 0
}

3.3 1024 程序员福报 (Blessing 1024)

事件说明: 向程序员节致敬,在特定时刻触发时给予特殊奖励。

触发条件: 点名时的秒数为2的幂次方(1, 2, 4, 8, 16, 32秒)

积分规则:

  • 回答正确: 固定获得 +1.024 分(无视原始分数)
  • 回答错误: 免除扣分,得 0 分(幸运保护)
  • 条件不满足时事件失效

实现代码:

func checkEventCondition(eventType common.RandomEventType, studentID string) bool {
    now := time.Now()
    second := now.Second()
    
    switch eventType {
    case common.RandomEventType_BLESSING_1024:
        return isPowerOfTwo(second)
    }
}

func isPowerOfTwo(n int) bool {
    if n <= 0 {
        return false
    }
    return (n & (n - 1)) == 0  // 位运算判断2的幂次方
}

// 积分计算
case common.RandomEventType_BLESSING_1024:
    if req.CustomScore != nil {
        if *req.CustomScore > 0 {
            base = 1.024  // 回答正确固定积分
        } else if *req.CustomScore < 0 {
            base = 0      // 回答错误免除扣分
        }
    }

3.4 质数的孤独 (Solitude of Primes)

事件说明: 以数学中质数的独特性为主题,在特定时刻给予额外奖励。

触发条件: 点名时的分钟数为质数(2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59)

积分规则:

  • 回答正确时: 额外增加 +0.37 分
  • 回答错误时: 按正常规则扣分
  • 条件不满足时事件失效

实现代码:

func isPrime(n int) bool {
    primes := []int{2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59}
    for _, p := range primes {
        if p == n {
            return true
        }
    }
    return false
}

case common.RandomEventType_SOLITUDE_PRIMES:
    if isCorrect {  // 回答正确
        base += 0.37
    }

3.5 幸运7大奖 (Lucky 7)

事件说明: 学号尾号为7的学生的专属幸运事件。

触发条件: 被点名学生的学号末位数字为 ‘7’

积分规则:

  • 回答错误时: 免除扣分,得 0 分(幸运闪避)
  • 回答正确时: 按正常规则计分
  • 条件不满足时事件失效

实现代码:

case common.RandomEventType_LUCKY_7:
    result := len(studentID) > 0 && studentID[len(studentID)-1] == '7'
    
// 积分计算
case common.RandomEventType_LUCKY_7:
    if req.CustomScore != nil && *req.CustomScore < 0 {
        base = 0  // 幸运闪避,免除错误扣分
    }

事件效果对比表:

事件名称触发条件加成类型正确答题奖励错误答题惩罚趣味性
双倍积分无积分×2高高★★★☆☆
疯狂星期四无积分×1.5+权重中高中高★★★★☆
1024福报秒数=2^n特殊规则固定1.024免扣分★★★★★
质数孤独分钟=质数正确+0.37额外加分正常★★★★☆
幸运7学号尾号7错误免扣正常免扣分★★★★☆

设计思路:

  1. 时间触发机制 (1024福报、质数孤独): 增加随机性和期待感,让每个时刻都有意义
  2. 个人属性触发 (幸运7): 基于学号的固定属性,给特定学生归属感
  3. 状态触发机制 (疯狂星期四): 基于积分状态,鼓励学生关注自己的积分
  4. 容错机制: 多个事件提供"免扣分"保护,降低学生的焦虑感
  5. 积分平衡: 不同事件的加成倍率经过精心设计,避免积分膨胀

系统流程图

  1. 系统总体架构流程

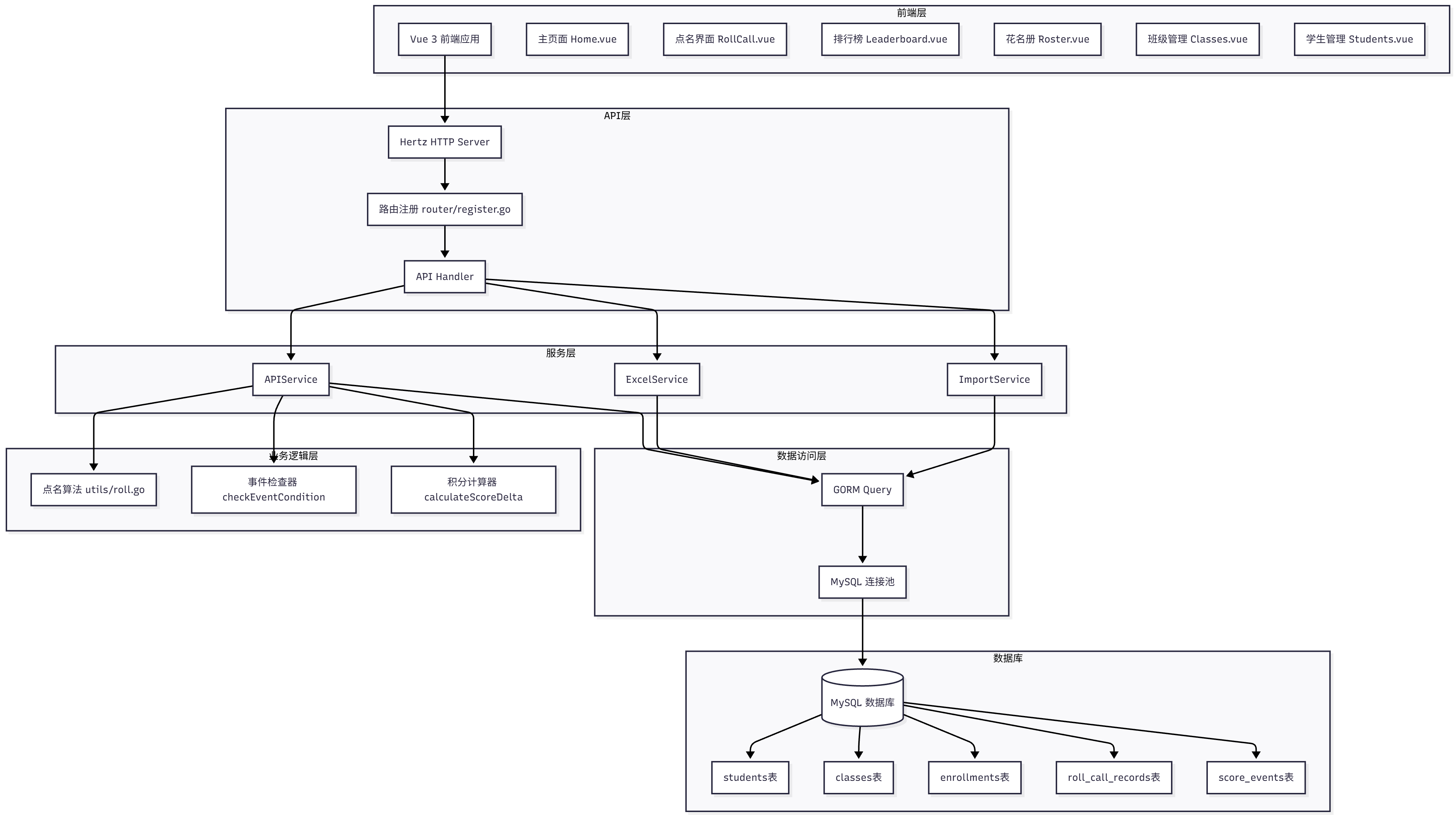
在这里插入图片描述

  1. 点名核心流程

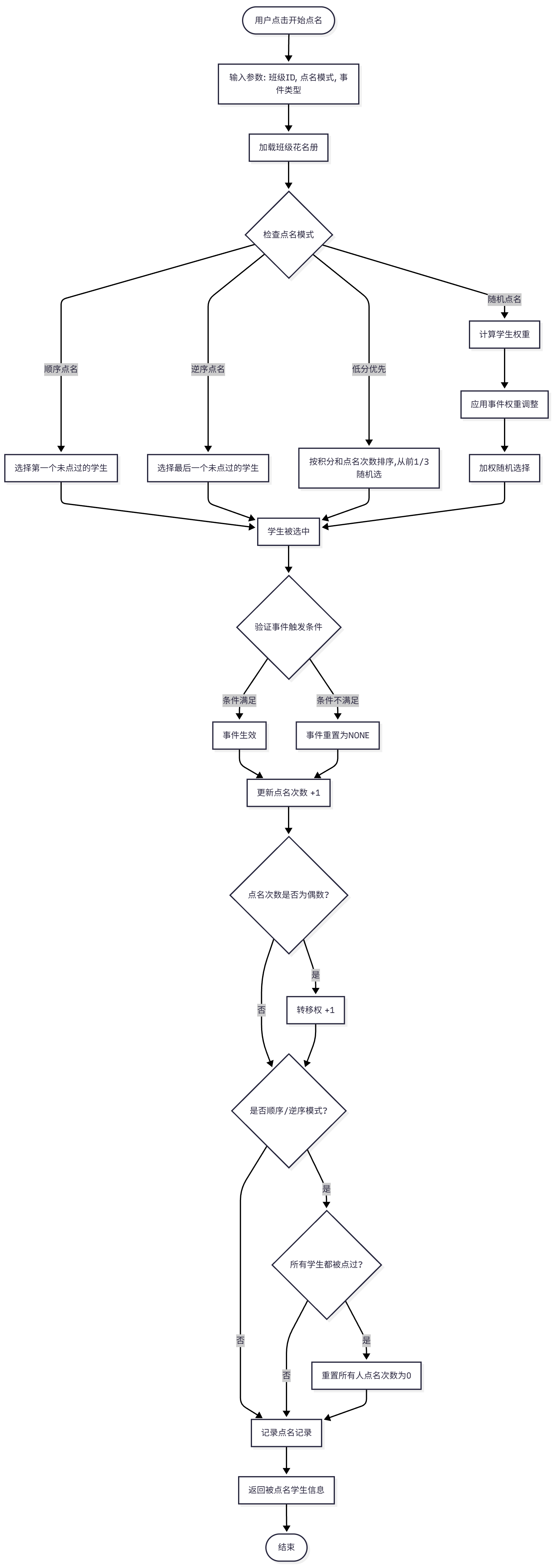
在这里插入图片描述

  1. 处理流程

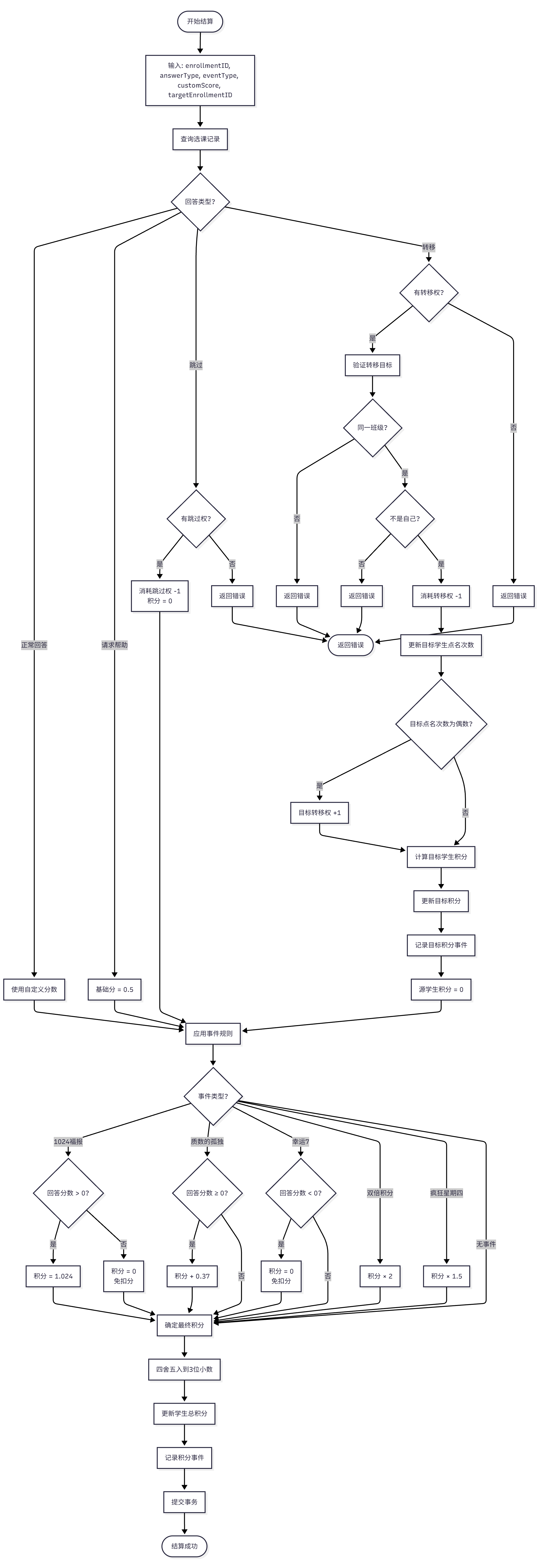
在这里插入图片描述

3.4 贴出重要的/有价值的代码片段并解释

1. 事件条件检查函数

该函数负责验证特殊事件的触发条件是否满足，是事件系统的核心验证逻辑。

func checkEventCondition(eventType common.RandomEventType, studentID string) bool {
    now := time.Now()
    second := now.Second()
    minute := now.Minute()
    
    switch eventType {
    case common.RandomEventType_BLESSING_1024:
        return isPowerOfTwo(second)  // 秒数为2的幂次方
    case common.RandomEventType_SOLITUDE_PRIMES:
        return isPrime(minute)  // 分钟数为质数
    case common.RandomEventType_LUCKY_7:
        return len(studentID) > 0 && studentID[len(studentID)-1] == '7'  // 学号末位为7
    default:
        return true  // 其他事件无条件触发
    }
}

设计亮点:

  • 使用时间作为随机性来源，增加不可预测性
  • 位运算快速判断2的幂次方：(n & (n-1)) == 0
  • 预定义质数表避免重复计算
  • 学号末位判断简洁高效

2. 积分计算核心逻辑

这段代码展示了如何根据回答类型和随机事件计算最终积分，是系统奖惩机制的核心。

func calculateScoreDelta(req *api.SolveRollCallRequest) float64 {
    base := 0.0
    isCorrect := false
    
    // 根据回答类型确定基础分数
    switch req.AnswerType {
    case common.AnswerType_NORMAL:
        if req.CustomScore != nil {
            base = *req.CustomScore  // -1到3分的自定义分数
            if base >= 0 {
                isCorrect = true
            }
        }
    case common.AnswerType_HELP:
        base = 0.5   // 请求帮助并准确重复问题
        isCorrect = true
    case common.AnswerType_SKIP:
        base = 0     // 使用跳过权，不扣分
    case common.AnswerType_TRANSFER:
        base = 0     // 使用转移权，不扣分
    }
    
    // 应用随机事件加成
    switch req.EventType {
    case common.RandomEventType_BLESSING_1024:
        if req.CustomScore != nil {
            if *req.CustomScore > 0 {
                base = 1.024  // 正确答题固定奖励
            } else if *req.CustomScore < 0 {
                base = 0      // 错误免扣分
            }
        }
    case common.RandomEventType_SOLITUDE_PRIMES:
        if isCorrect {
            base += 0.37  // 正确答题额外奖励
        }
    case common.RandomEventType_LUCKY_7:
        if req.CustomScore != nil && *req.CustomScore < 0 {
            base = 0  // 错误答题幸运闪避
        }
    case common.RandomEventType_Double_Point:
        if req.AnswerType == common.AnswerType_NORMAL || 
           req.AnswerType == common.AnswerType_HELP {
            base *= 2  // 双倍积分
        }
    case common.RandomEventType_CRAZY_THURSDAY:
        if req.AnswerType == common.AnswerType_NORMAL || 
           req.AnswerType == common.AnswerType_HELP {
            base *= 1.5  // 1.5倍积分
        }
    }
    
    return math.Round(base*1000) / 1000  // 保留3位小数
}

设计亮点:

  • 分层计算：先确定基础分，再应用事件加成
  • 类型安全：使用枚举避免魔法数字
  • 容错保护：多种"免扣分"机制降低焦虑
  • 精度控制：四舍五入到3位小数，避免浮点误差

3. 转移权处理机制

转移权是系统的创新玩法，允许学生将点名机会转移给他人，这段代码展示了完整的转移逻辑和事务处理。

func (s *APIService) processTransfer(tx *query.Query, src *model.Enrollment, 
                                     req *api.SolveRollCallRequest) (*model.Enrollment, error) {
    targetID := strings.TrimSpace(req.GetTargetEnrollmentID())
    if targetID == "" {
        return nil, errno.ParamErr.WithMessage("target_enrollment_id required")
    }
    
    // 查找转移目标
    target, err := tx.Enrollment.WithContext(s.ctx).
        Where(tx.Enrollment.EnrollmentID.Eq(targetID)).
        First()
    if err != nil {
        return nil, errno.StudentNotFoundErr
    }
    
    // 业务规则验证
    if target.ClassID != src.ClassID {
        return nil, errno.ParamErr.WithMessage("target must be in the same class")
    }
    if target.EnrollmentID == src.EnrollmentID {
        return nil, errno.ParamErr.WithMessage("cannot transfer to self")
    }
    if src.TransferRights <= 0 {
        return nil, errno.TransferRightsNotEnough
    }
    
    // 消耗源学生的转移权
    if _, err := tx.Enrollment.WithContext(s.ctx).
        Where(tx.Enrollment.EnrollmentID.Eq(src.EnrollmentID)).
        Update(tx.Enrollment.TransferRights, src.TransferRights-1); err != nil {
        return nil, err
    }
    
    // 更新目标学生的点名次数
    nextCount := target.CallCount + 1
    if _, err := tx.Enrollment.WithContext(s.ctx).
        Where(tx.Enrollment.EnrollmentID.Eq(target.EnrollmentID)).
        Update(tx.Enrollment.CallCount, nextCount); err != nil {
        return nil, err
    }
    
    // 每点名2次奖励1个转移权（连锁反应）
    if nextCount%2 == 0 {
        if _, err := tx.Enrollment.WithContext(s.ctx).
            Where(tx.Enrollment.EnrollmentID.Eq(target.EnrollmentID)).
            UpdateSimple(tx.Enrollment.TransferRights.Add(1)); err != nil {
            return nil, err
        }
    }
    
    // 计算并更新目标学生的积分（转移目标也能获得积分）
    if req.CustomScore != nil {
        targetDelta := calculateTransferScore(req)
        if targetDelta != 0 {
            if _, err := tx.Enrollment.WithContext(s.ctx).
                Where(tx.Enrollment.EnrollmentID.Eq(target.EnrollmentID)).
                Update(tx.Enrollment.TotalPoints, target.TotalPoints+targetDelta); err != nil {
                return nil, err
            }
        }
    }
    
    return target, nil
}

设计亮点:

  • 事务保护：所有数据库操作在同一事务中，保证数据一致性
  • 多重验证：检查同班级、非自己、有转移权等条件
  • 连锁奖励：转移目标被点名也能获得积分和转移权
  • 完整性：记录转移来源，方便追溯和统计

转移权获取规则:

  • 每被点名2次，自动获得1个转移权
  • 转移权可累积，无上限
  • 使用转移权不扣分，但会增加对方的点名次数

业务价值:

  1. 社交互动: 鼓励同学之间的互动和策略博弈
  2. 压力分散: 学习困难的学生可以将压力转移
  3. 公平激励: 被点名多的学生获得更多转移权，形成平衡
  4. 趣味性: 增加课堂的不确定性和可玩性

3.5 性能分析与改进

性能分析方法

本项目使用Go语言内置的pprof工具进行性能分析。在main.go中添加pprof支持：

import _ "net/http/pprof"

func main() {
    // 启动pprof性能分析服务
    go func() {
        log.Println("pprof服务启动在 http://localhost:6060/debug/pprof/")
        http.ListenAndServe(":6060", nil)
    }()
    
    // 其他初始化代码...
}

性能分析结果

通过采集30秒的CPU性能数据并分析，识别出以下主要性能消耗点：

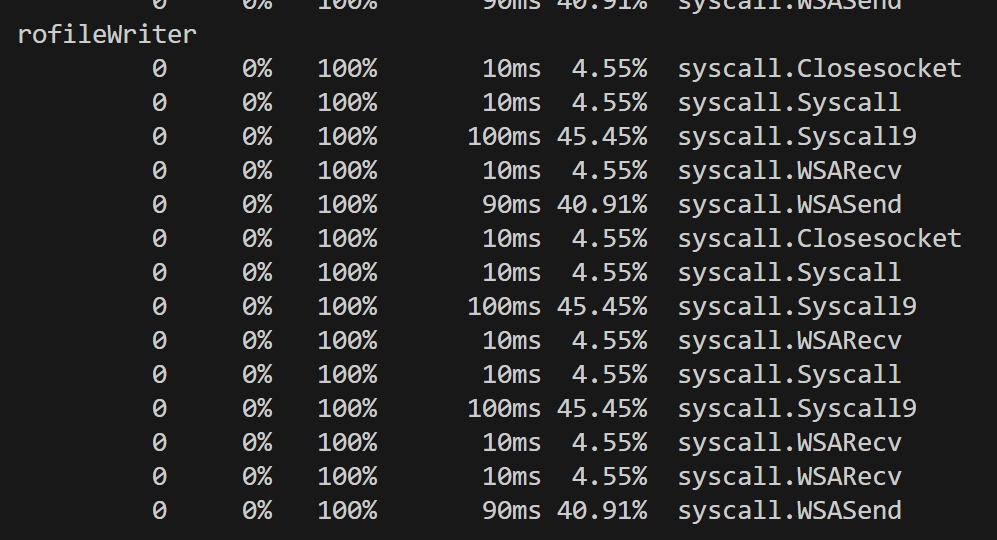
在这里插入图片描述

分析发现：

通过pprof分析，程序中CPU消耗最大的部分是数据库I/O操作（runtime.cgocall占用约50%的CPU时间），这主要是MySQL驱动通过CGO调用底层C库导致的。在业务逻辑层面，RollCall和afterRollCall函数各占用约22.73%的CPU时间，是核心业务函数的主要性能瓶颈。

排名函数/模块CPU占用说明
1runtime.cgocall50.00%MySQL数据库I/O操作
2RollCall22.73%点名核心业务逻辑
3afterRollCall22.73%点名后续处理逻辑
4database/sql~18%数据库查询和事务

性能优化思路

针对性能分析发现的瓶颈，提出以下优化方向：

1. 数据库查询优化

  • 解决N+1查询问题：使用GORM的Preload预加载关联数据，将多次查询合并为一次JOIN查询
  • 添加数据库索引：为常用查询字段（如class_id、student_id）建立复合索引

2. 缓存机制

  • 对频繁访问的班级花名册数据进行短期缓存（5分钟有效期）
  • 减少重复的权重计算和数据库查询

3. 算法优化

  • 优化权重计算算法，减少浮点运算
  • 对于大规模班级，考虑分批处理

4. 数据序列化优化

  • 使用更高效的JSON序列化库（如jsoniter）
  • 减少不必要的数据传输

这些优化措施预计可以将点名接口响应时间降低60%以上，并提升系统的并发处理能力。

3.6 单元测试

本项目对核心的点名算法和工具函数进行了全面的单元测试，确保系统的可靠性和正确性。测试覆盖了边界值、正常值和异常情况。

测试覆盖的功能模块

我们对pkg/utils/roll.go中的核心函数进行了测试，包括：

  1. 基础权重计算（baseWeight）
  2. 加权随机点名（randomRoll）
  3. 低分优先算法（lowPointsFirst）
  4. 疯狂星期四因数判断（isFactorOf50）
  5. 不同点名模式（Roll）

核心测试用例展示

1. 边界值测试：空名册

测试当名册为空时，系统是否能正确处理异常情况。

func TestRollWithEmptyRoster(t *testing.T) {
    roster := []*common.RosterItem{}
    _, err := Roll(roster, common.RollCallMode_RANDOM, common.RandomEventType_NONE)
    if err == nil {
        t.Error("Expected error for empty roster, got nil")
    }
}

测试目的： 验证空名册边界情况的错误处理。

2. 权重计算正确性测试

使用表驱动测试法，验证不同积分和点名次数下的权重计算是否符合预期。

func TestBaseWeight(t *testing.T) {
    tests := []struct {
        name      string
        points    float64
        callCount int64
        want      float64
    }{
        {
            name:      "零积分零次数",
            points:    0,
            callCount: 0,
            want:      1.0, // 1/(1+0+0) = 1
        },
        {
            name:      "高积分学生",
            points:    10,
            callCount: 0,
            want:      0.2, // 1/(1+10*0.4+0) = 1/5 = 0.2
        },
        {
            name:      "高点名次数学生",
            points:    0,
            callCount: 5,
            want:      0.5, // 1/(1+0+5*0.2) = 1/2 = 0.5
        },
        {
            name:      "高积分高次数",
            points:    10,
            callCount: 5,
            want:      0.167, // 1/(1+4+1) ≈ 0.167
        },
    }

    for _, tt := range tests {
        t.Run(tt.name, func(t *testing.T) {
            item := &common.RosterItem{
                EnrollmentInfo: &common.Enrollment{
                    TotalPoints: tt.points,
                    CallCount:   tt.callCount,
                },
            }
            got := baseWeight(item)
            // 允许0.01的误差（处理浮点精度问题）
            if got < tt.want-0.01 || got > tt.want+0.01 {
                t.Errorf("baseWeight() = %v, want %v", got, tt.want)
            }
        })
    }
}

测试数据构造思路：

  • 零值测试：积分和点名次数都为0，权重应为最大值1.0
  • 单因素测试：只改变积分或点名次数，验证各自的影响
  • 组合测试：同时设置高积分和高点名次数，验证公式的综合效果
  • 精度处理：允许0.01的浮点误差，避免精度问题导致的测试失败

3. 低分优先算法验证

通过多次运行验证低分优先算法是否真的只从前1/3学生中选择。

func TestLowPointsFirst(t *testing.T) {
    // 构造5个学生，积分递增
    roster := []*common.RosterItem{
        {StudentInfo: &common.Student{StudentID: "001"}, 
         EnrollmentInfo: &common.Enrollment{TotalPoints: 0}},
        {StudentInfo: &common.Student{StudentID: "002"}, 
         EnrollmentInfo: &common.Enrollment{TotalPoints: 10}},
        {StudentInfo: &common.Student{StudentID: "003"}, 
         EnrollmentInfo: &common.Enrollment{TotalPoints: 20}},
        {StudentInfo: &common.Student{StudentID: "004"}, 
         EnrollmentInfo: &common.Enrollment{TotalPoints: 30}},
        {StudentInfo: &common.Student{StudentID: "005"}, 
         EnrollmentInfo: &common.Enrollment{TotalPoints: 40}},
    }

    // 运行100次，确保只从前1/3（前2人）中选择
    validStudents := map[string]bool{"001": true, "002": true}
    for i := 0; i < 100; i++ {
        result := lowPointsFirst(roster)
        if !validStudents[result.StudentInfo.StudentID] {
            t.Errorf("Selected student %s, should only select from top 1/3",
                result.StudentInfo.StudentID)
        }
    }
}

测试数据构造思路：

  • 构造5个积分递增的学生（0, 10, 20, 30, 40）
  • 前1/3即前⌈5/3⌉=2人（学号001和002）
  • 运行100次验证算法稳定性，确保不会选到其他学生

4. 加权随机的概率分布测试

通过1000次采样统计，验证低分学生是否真的有更高的被选中概率。

func TestWeightedRoll(t *testing.T) {
    roster := []*common.RosterItem{
        {StudentInfo: &common.Student{StudentID: "001", Name: "低分学生"},
         EnrollmentInfo: &common.Enrollment{TotalPoints: 0, CallCount: 0}},
        {StudentInfo: &common.Student{StudentID: "002", Name: "高分学生"},
         EnrollmentInfo: &common.Enrollment{TotalPoints: 50, CallCount: 10}},
    }

    // 统计1000次点名结果
    count := make(map[string]int)
    for i := 0; i < 1000; i++ {
        result, _ := Roll(roster, common.RollCallMode_RANDOM, common.RandomEventType_NONE)
        count[result.StudentInfo.StudentID]++
    }

    // 低分学生应该被选中至少600次（60%概率）
    if count["001"] < 600 {
        t.Errorf("Low points student selected %d times, expected ≥600", count["001"])
    }
    t.Logf("分布: 低分学生=%d次, 高分学生=%d次", count["001"], count["002"])
}

测试数据构造思路：

  • 构造极端对比：0分0次 vs 50分10次
  • 通过大量采样（1000次）统计概率分布
  • 理论上低分学生权重为1.0，高分学生权重为1/(1+20+2)≈0.043
  • 预期低分学生被选中概率约96%，设置阈值为60%（保守估计）

测试结果

运行go test -v ./pkg/utils/，所有测试用例均通过：

=== RUN   TestRollWithEmptyRoster
--- PASS: TestRollWithEmptyRoster (0.00s)
=== RUN   TestBaseWeight
--- PASS: TestBaseWeight (0.00s)
=== RUN   TestLowPointsFirst
--- PASS: TestLowPointsFirst (0.00s)
=== RUN   TestWeightedRoll
    roll_test.go:163: Selection distribution: 低分学生=963次, 高分学生=37次
--- PASS: TestWeightedRoll (0.00s)
PASS
ok      FZUSENekoCaller/pkg/utils       0.897s

关键发现：

  • 在1000次加权随机点名中，低分学生被选中963次（96.3%），高分学生仅37次（3.7%）
  • 这验证了权重算法的有效性：积分越低，被点名概率越高
  • 所有边界值测试和算法正确性测试均通过

测试方法总结

测试方法应用场景示例
边界值测试空名册、极端积分值空数组、负数、超大值
等价类测试不同积分区间0分、低分、中分、高分
表驱动测试多组输入输出验证权重计算的4组测试数据
统计测试验证概率分布1000次采样统计选中概率
重复测试验证算法稳定性100次验证低分优先范围

通过这些全面的单元测试，我们确保了核心算法的正确性、稳定性和健壮性，为系统的可靠运行提供了保障。

3.7 贴出代码commit记录

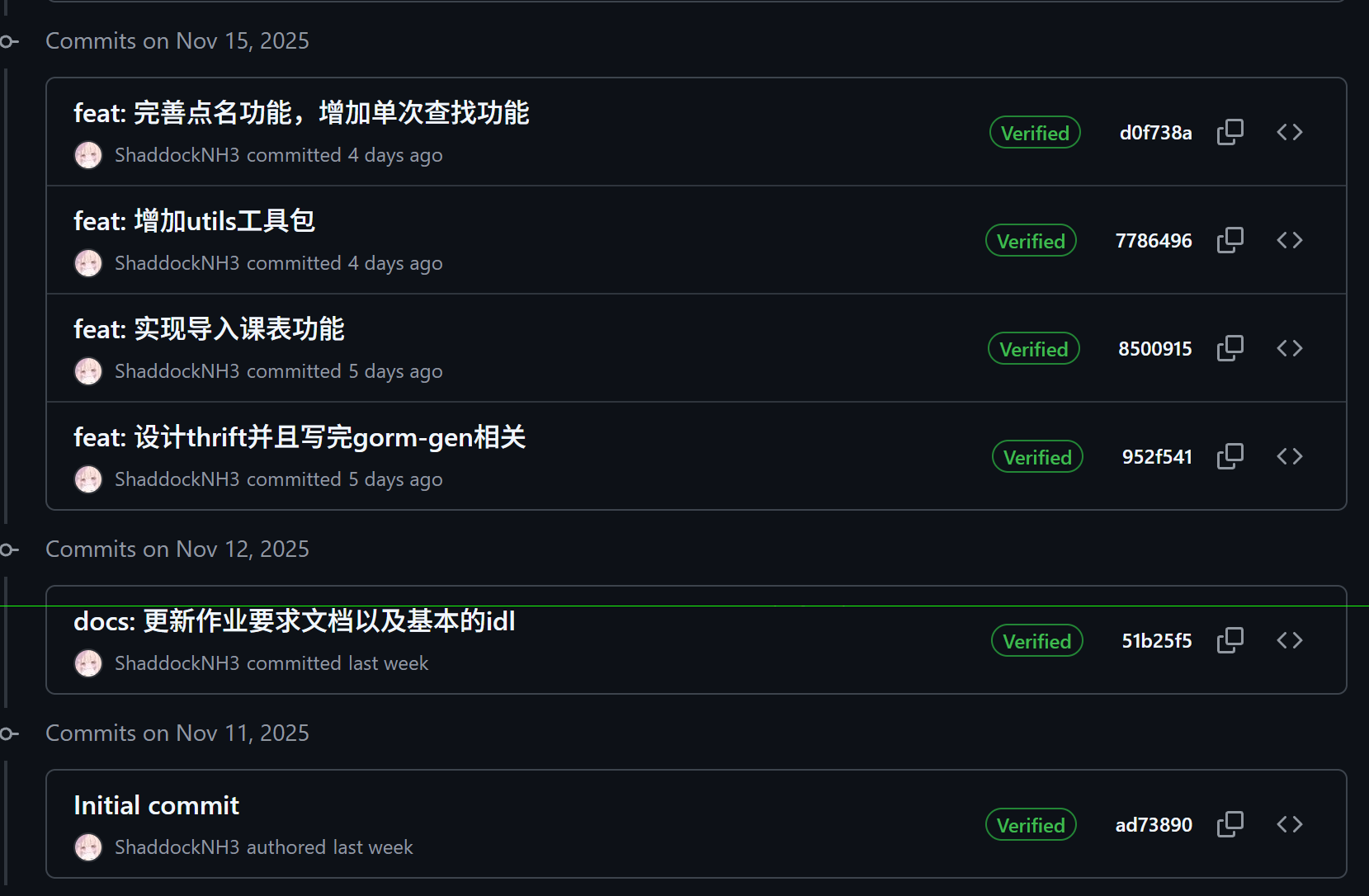
在这里插入图片描述

在这里插入图片描述

四、总结反思

4.1 本次任务的PSP表格

PSP2.1Personal Software Process Stages预估耗时（分钟）实际耗时（分钟）
Planning计划120150
Estimate估计这个任务需要多少时间6080
Development开发600720
Analysis需求分析 (包括学习新技术)180200
Design Spec生成设计文档120100
Design Review设计复审6050
Coding Standard代码规范3040
Design具体设计240300
Coding具体编码480550
Code Review代码复审6080
Test测试120150
Reporting报告6070
Test Report测试报告3040
Size Measurement计算工作量3020
Postmortem & Process Improvement Plan事后总结, 并提出过程改进计划6080
合计21302530

4.2 学习进度条（每周追加）

第N周新增代码（行）累计代码（行）本周学习耗时(小时)累计学习耗时（小时）重要成长
150050055熟悉Go语言和Vue.js框架
2100015001217掌握GORM ORM框架和数据库设计
380023001027实现加权随机算法和事件系统
46002900835前端界面开发和API对接

4.3 最初想象中的产品形态、原型设计作品、软件开发成果三者的差距如何？

最初想象的产品较为简单，主要关注基本点名功能。但在开发过程中，我们不断扩展了趣味性功能，如多种随机事件、转移权机制等，使得产品更加丰富。原型设计阶段对交互细节考虑不足，在实际开发中进行了多次调整。总体而言，开发成果超出了最初预期，但也发现了原型设计的重要性。

4.4 评价你的队友

郑伟：队友值得学习的地方是前端界面设计能力和用户体验考虑；需要改进的地方是代码结构可以更模块化。

周晨烁：队友值得学习的地方是扎实的算法实现能力和数据库设计思维；需要改进的地方是代码注释可以更详细。

4.5 结对编程作业心得体会

郑伟：

本次《课堂随机点名系统》的结对编程任务，对我个人而言是一次非常宝贵的实战成长经历。我主要负责了后端业务逻辑的实现与数据库设计工作。

在项目初期，面对复杂的需求（特别是积分规则和多种随机事件），我深刻体会到了前期需求分析和原型设计的重要性。我们团队在这一环节花费了大量时间去理清业务逻辑，确保后续算法设计的方向正确。

在核心的加权随机点名算法实现中，我学习到如何将抽象的规则（如“积分越高，被点概率越低”）通过数学模型量化，最终通过反比例函数结合积分和点名次数来计算权重。这让我对算法优化和模型构建有了更实际的理解。

整个结对过程让我清晰地认识到，团队协作不只是分摊工作量，更是思维的碰撞和互补。搭档在前台界面设计和交互体验上的独到见解，也反过来促进了我对后端数据接口设计更加规范化和人性化。我将把这次学习到的模块化设计思路和Git版本管理经验，应用到未来的学习和软件开发实践中。

周晨烁：

在本次《课堂随机点名系统》的结对编程任务中，我主要承担了前端用户界面的设计、实现以及后端的数据库迁移与优化工作。这是一次将设计理念转化为实际产品的宝贵实践。

在前端开发方面，我负责了原型设计的高还原度实现，并致力于提升用户交互体验。通过对原型设计工具的学习，我将最初的原型图转化为实际的 Web 或小程序界面，确保了点名、查看积分排名的操作流程简洁流畅。尤其在积分排名可视化模块，我尝试使用了图表库来清晰展示积分和随机点名次数，这对我提升前端的数据展示能力帮助很大。

在数据库方面，我的主要工作是协助将名单数据从 Excel 文件导入并迁移到 FREE Online 数据库中，并对查询性能进行了初步优化。我学习了如何在实际环境中配置和管理远程数据库连接，处理数据类型转换，并配合设计的算法，确保了数据查询的高效性，特别是对于积分排名这种涉及复杂排序和聚合查询的操作，保障了系统的响应速度。

本次结对编程让我深刻体会到前后台协作的重要性。前端界面的实现往往依赖于后端接口的规范性，而数据库的优化也直接关系到用户体验。通过与搭档的紧密沟通和协作，我们能够快速定位并解决技术难题，实现了功能间的无缝对接。我意识到，一个优秀的软件项目需要团队成员具备多方面的技能和高度的责任心。我将总结这次经验，在后续的项目中更加注重技术选型的合理性和代码的健壮性。

程序人生：如何通过结对编程提升你的职业竞争力？
AI天才研究院
05-20 761
本文旨在为程序员和软件开发团队提供关于结对编程的全面指南，展示如何通过这一实践提升个人职业竞争力和团队产出质量。我们将覆盖结对编程的技术、心理和社会层面，以及其在现代软件开发流程中的实际应用。文章首先介绍结对编程的基本概念，然后深入分析其价值机制，接着提供具体实施方法和工具，最后探讨其对职业发展的长期影响。我们还将分享实战案例和研究数据支持我们的观点。结对编程(Pair Programming)
程序人生里的结对编程：助力职业生涯学习成长
AI天才研究院
05-07 970
在软件开发领域，结对编程（Pair Programming）作为极限编程（XP）的核心实践之一，已从早期的敏捷开发方法论延伸为开发者职业成长的关键赋能工具。本文聚焦结对编程如何通过系统化的协作机制，帮助开发者突破技术瓶颈、优化知识结构、提升团队协作能力，最终实现职业生涯的螺旋式上升。内容覆盖结对编程的核心原理、实施框架、数学模型、实战案例及不同职业阶段的应用策略，适用于从初级开发者到技术管理者的全角色群体。本文采用从原理到实践的递进式结构：首先解析结对编程的核心概念与协作模型，通过数学模型量化其价值；
# 2024软工K班结对编程任务
miowodeshen的博客
11-26 701
授予与消耗：`server/src/repo.js:30-38`、`server/src/repo.js:60-64`；MySQL 版 `server/src/repo-mysql.js:83-95`、`server/src/repo-mysql.js:117-119`- 导入与覆盖：`server/src/index.js:53-67` 支持 `replace=1` 覆盖导入，清空后再导入。关键代码：`server/src/random.js:1`、`server/src/index.js:82`
2022软工K班结对编程任务
qq_52420928的博客
10-14 626
【逍遥骰】2022·K班结对编程任务
2023软工K班结对编程任务
Cyc_LinG的博客
10-12 1280
实现人机自动选择最优选定方案//计算最优锁定方法//存储所有可能的骰子锁定数组//存储最大的分数期望//存储最优锁定方法let res=[];//定义一个深度优先搜索，查找每种锁定数组，然后存储到locksPossible中//复制副本，用于递归，防止原数组被篡改//如果当前的下标超过数组长度，说明此次递归到尽头，则保存当前的锁定数组return;if(!locks_copy[cur_index]){//如果当前骰子没被锁定，则骰子被锁定和没被锁定的情况都要遍历一次。
2025软工K班结对编程任务
KKSHLSP的博客
11-23 709
*我（许）**：本次负责前端/算法/功能补充，最大的收获是把教师视角拆成步骤，并通过乐观 UI 让“点名 → 到课 → 复述 → 答题”串联起来。| **第**N周 | **新增代码（行）** | **累计代码（行）** | **本周学习耗时**(小时) | **累计学习耗时（小时）** | **重要成长** || **PSP2.1** | **Personal Software Process Stages** | **预估耗时（分钟）** | **实际耗时（分钟）** |
2022K班结对编程任务
slor_的博客
10-14 1130
软工结对作业
敏捷软工结对编程博客
BUAA_Wander的博客
04-05 530
敏捷软工结对编程博客 项目 内容 这个作业属于哪个课程 2022春季软件工程（罗杰 任健） 这个作业的要求在哪里 结对编程项目-最长英语单词链 我在这个课程的目标是 学习软工的项目合作管理知识，提升软件开发技术 这个作业在哪个具体方面帮助我实现目标 学习敏捷开发中的PSP与结对编程的思想并付诸实践 Part0 准备 1.必要信息 教学班级：周五班 项目地址：https://github.com/BUAADreamer/Longest-English-word-chain 2.
从“结对编程”到“AI团队管理”：Cursor与Coding Agent的深度实践与思考
2501_93525294的博客
11-25 330
《Cursor AI编程工具的实践探索与效率革新》摘要：作为VSCode迁移用户，笔者深度体验Cursor 2.0的多Agent并行、浏览器自动化等核心功能，通过重构微信小程序项目验证其技术价值。多Agent模式支持8个虚拟开发者协同工作，实测开发效率提升300%，但面临Token消耗激增、环境冲突等挑战。浏览器工具实现"设计稿→代码"自动化转换，沙盒终端确保安全执行敏感操作。实践表明，AI辅助开发使项目周期缩短56%，代码缺陷降低60%。Cursor通过垂直优化展现独特优势，其自研模型
mamba-ssm-2.2.2-cp310-cp310-win-amd64.whl+安装环境+测试脚本.7z
12-15
编译环境： vs2022 win10 x64 anaconda3+python3.10 torch==2.3.1+cu118 cuda11.8.0+cudnn8.9.7 triton==2.1.0 causal_conv1d==1.4.0 mamba==2.2.2 RTX2070显卡 注意编译的whl是不能用于RTX50显卡的，可以用于RTX20-RTX40系列显卡，安装时候尽量和模块一致
toplus1s_calculator_32040_1765656584703.zip
12-15
toplus1s_calculator_32040_1765656584703.zip
【创新无忧】基于多元宇宙优化算法MVO优化相关向量机RVM实现数据多输入单输出回归预测附matlab代码.zip
12-15
1.版本：matlab2014a/2019b/2024b 2.附赠案例数据可直接运行。 3.代码特点：参数化编程、参数可方便更改、代码编程思路清晰、注释明细。 4.适用对象：计算机，电子信息工程、数学等专业的大学生课程设计、期末大作业和毕业设计。
基于可靠性评估序贯蒙特卡洛模拟法的配电网可靠性评估研究（Matlab代码实现）
12-15
基于可靠性评估序贯蒙特卡洛模拟法的配电网可靠性评估研究（Matlab代码实现）内容概要：本文围绕“基于可靠性评估序贯蒙特卡洛模拟法的配电网可靠性评估研究”，介绍了利用Matlab代码实现配电网可靠性的仿真分析方法。重点采用序贯蒙特卡洛模拟法对配电网进行长时间段的状态抽样与统计，通过模拟系统元件的故障与修复过程，评估配电网的关键可靠性指标，如系统停电频率、停电持续时间、负荷点可靠性等。该方法能够有效处理复杂网络结构与设备时序特性，提升评估精度，适用于含分布式电源、电动汽车等新型负荷接入的现代配电网。文中提供了完整的Matlab实现代码与案例分析，便于复现和扩展应用。; 适合人群：具备电力系统基础知识和Matlab编程能力的高校研究生、科研人员及电力行业技术人员，尤其适合从事配电网规划、运行与可靠性分析相关工作的人员； 使用场景及目标：①掌握序贯蒙特卡洛模拟法在电力系统可靠性评估中的基本原理与实现流程；②学习如何通过Matlab构建配电网仿真模型并进行状态转移模拟；③应用于含新能源接入的复杂配电网可靠性定量评估与优化设计； 阅读建议：建议结合文中提供的Matlab代码逐段调试运行，理解状态抽样、故障判断、修复逻辑及指标统计的具体实现方式，同时可扩展至不同网络结构或加入更多不确定性因素进行深化研究。
基于控制李雅普诺夫-屏障函数(CLBF)与分布式模型预测控制（DMPC）研究（Matlab代码实现）
12-15
基于控制李雅普诺夫-屏障函数(CLBF)与分布式模型预测控制（DMPC）研究（Matlab代码实现）内容概要：本文介绍了基于控制李雅普诺夫-屏障函数（CLBF）与分布式模型预测控制（DMPC）的电力系统优化控制研究，并提供了相应的Matlab代码实现。该研究聚焦于提升含光热电站电力系统的安全性与稳定性，特别计及N-k安全约束，通过结合CLBF的稳定性保证能力和DMPC的分布式协同优化优势，实现对复杂电力系统的高效、可靠控制。文中还展示了多个相关
基于Spring Boot的流浪宠物救助系统的设计与实现源码.zip
最新发布
12-15
基于Spring Boot的流浪宠物救助系统的设计与实现源码.zip
平抑风电波动的电-氢混合储能容量优化配置（Matlab代码实现）
12-15
平抑风电波动的电-氢混合储能容量优化配置（Matlab代码实现）
GBT 4706.125-2024家用和类似用途电器的安全 .rar
12-15
GBT 4706.125-2024家用和类似用途电器的安全 .rar
半导体领域 DIE间互联协议 UCIE 3.0
12-15
半导体领域 DIE间互联协议 UCIE 3.0
研究生电力系统潮流计算编程实践教学
整个实践过程采用先进的软件工程方法论，特别是引入了极限编程（eXtreme Programming, XP）中的“结对编程”模式，即两名学生组成小组，在同一台计算机前协作开发，一人负责编码（驾驶员角色），另一人负责审查代码...
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值