Unbutu下学习树

Unbutu下学习树

---

一、树是什么？

树(Tree) 是n(n>=0)个节点的有限集合T，它满足两个条件：
1、有且仅有一个特定的称为根(root)的节点；
2、其余的节点可以分为m(m>=0)个互不相交的有限集合T1、T2…Tm，
其中每一个集合又是一颗树，并称为其根的子树
表示方法：树形表示法、目录表示法

1、树的示意图

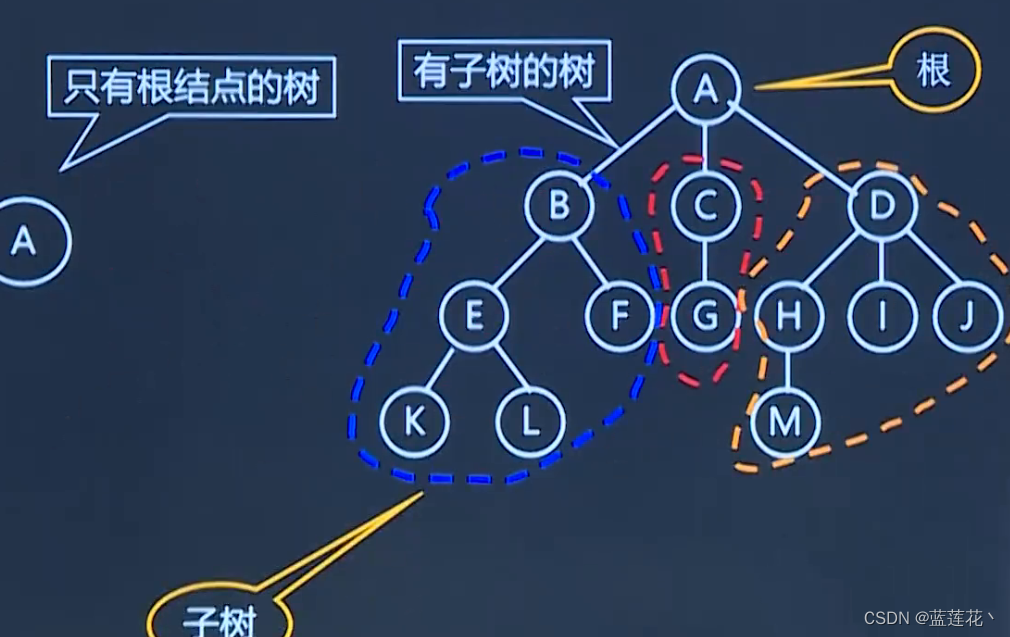
2、树的描述

1、一个节点的子树的个数称为该节点的度数
2、一颗树的度数是指该树中节点的最大度数
3、度数为零的节点称为树叶或者终端节点
4、度数不为零的节点称为分支节点
5、除根节点外的分支节点称为内部节点

3、节点关系示意图

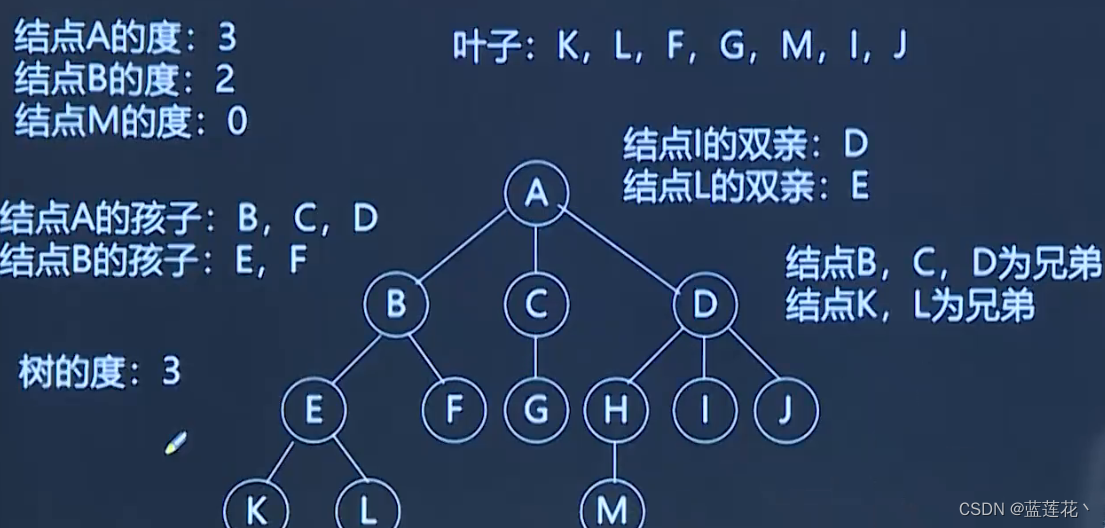
4、树的路径

1、树中节点层数的最大值称为该树的高度或深度。
2、树中任何节点都可以有零个或多个直接后继节点(子节点)，但至少只有一个直接前趋节点（父节点），根节点没有前趋节点，叶节点没有后继节点。

二、二叉树是什么？

二叉树是n(n>=0)个节点的有限集合，或者是空集(n=0)
或者是一个根节点以及两棵互不相交的，分别称为左子树和右子树的二叉树组合
严格区分左或者和右孩子，即使只有一个子节点也有区分左右。

1.二叉树示意图

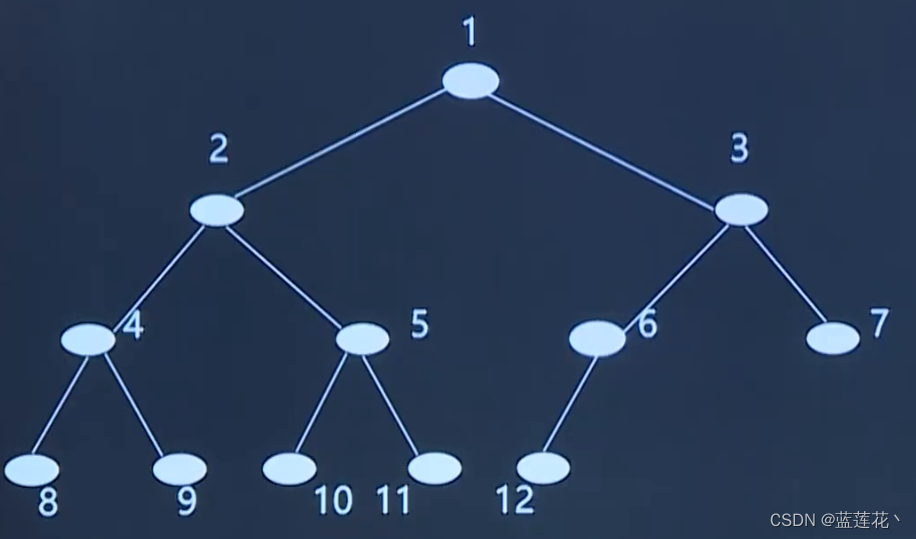
2.二叉树的性质

二叉树第i(i>=1)层上的节点最多为2^(i-1)个。
深度为k(k>=1)的二叉树最多有2^k-1个节点。
性质：
满叉数：深度为k(k>=1)时有2^(k-1)个节点的二叉树。
完全二叉树：只有最下面两层有度数小于2的节点，且最下面的一层
叶节点集中在最左边的若干位置上。
具有n个节点的完全二叉树的深度为
(log2n) +1 或 log2(n+1)

3.二叉树-顺序存储

顺序存储结构：完全二叉树节点的编号方法是从上到下，从左到右，根节点为1号节点。设完全二叉树的节点数为n，某节点编号为i
当 i>1(不是根节点)时，有父节点，其编号为 i/2
当2i<=n，有左孩子，其编号为2i，否则没有左孩子，本身是叶节点
当2i+1<=n，有右孩子，其编号为2i+1，否则没有右孩子
当i为奇数不为1，有左兄弟，其编号为i-1，否则没有左兄弟
当i为偶数小于n时，有右兄弟，其编号为i+1，否则没有右兄弟

4.二叉树遍历

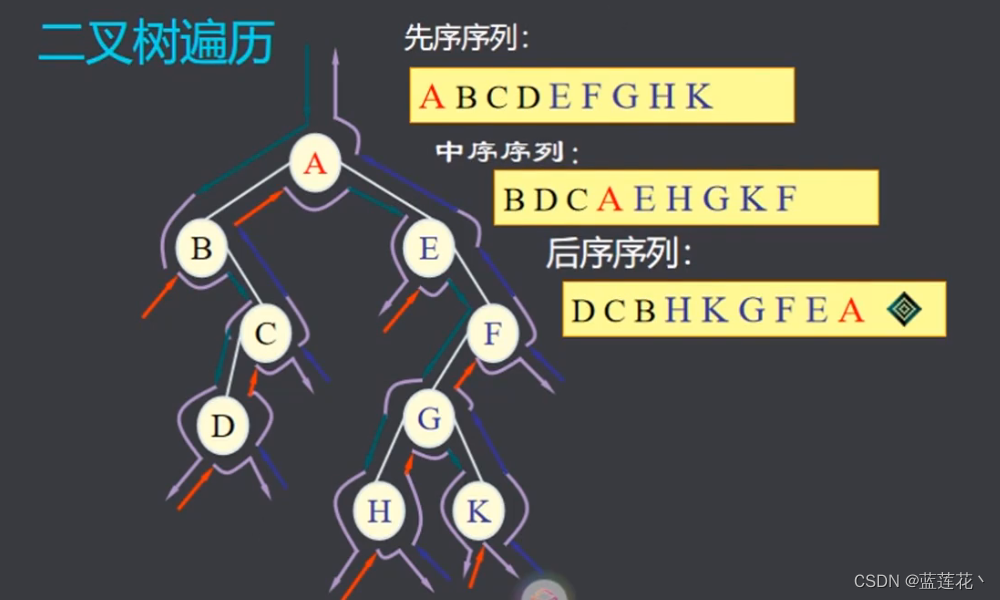
5.实例

1、创造接口文件:tree.h

2、实现接口文件:tree.c

3、测试文件:test.c

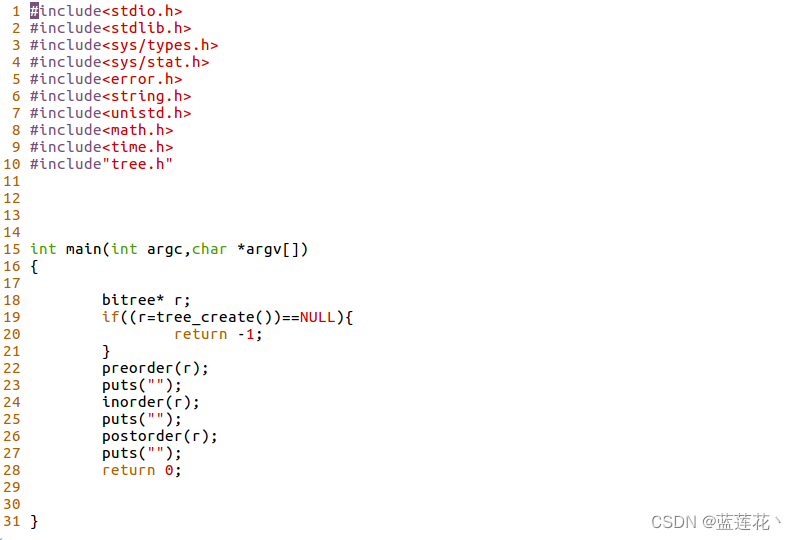
4、执行结果

5、层次遍历

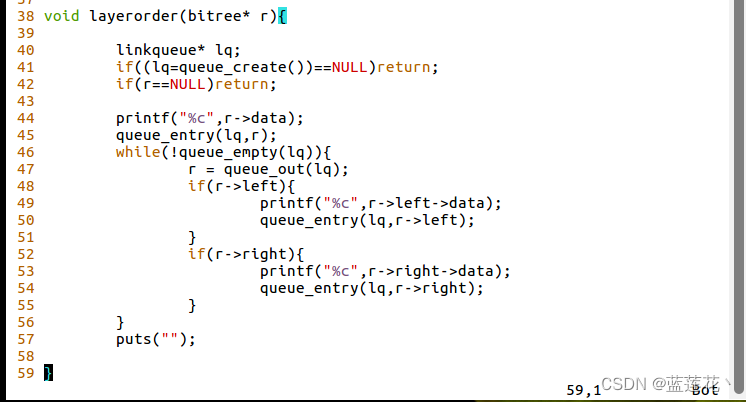
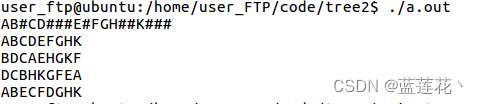
注意：重复调用头文件时

---