排序 - - - 选择排序（简单选择、堆排序）

选择排序：

基本原理:  将待排序的元素分为已排序(初始为空)和未排序两组，依次将未排序的元素中值最小的元素放入已排序的组中。

 

---

 

 简单选择排序：

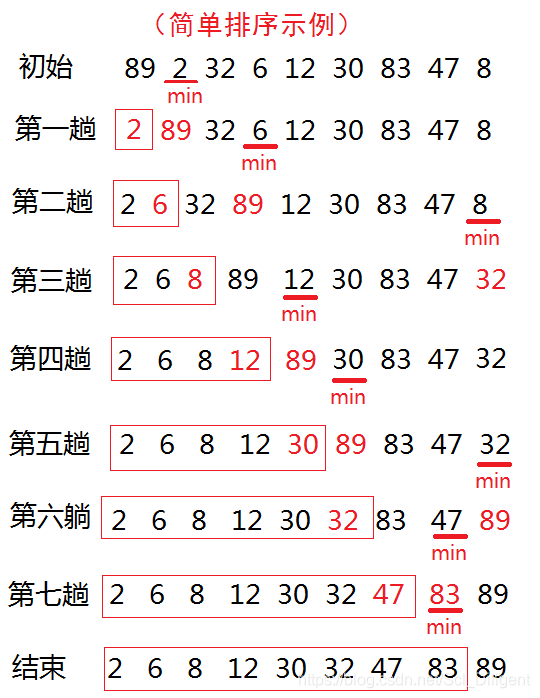
简单选择排序的基本过程为：

(1)在一组元素R[i]到R[n]中选择具有最小关键码的元素

(2)若它不是这组元素中的第一个元素，则将它与这组元素中的第一个元素对调。

(3)除去具有最小关键字的元素，在剩下的元素中重复第(1)、(2)步，直到剩余元素只有一个为止。

 

void SimpleSelectSort(int* arr, int len)
{
	for(int i = 0; i < len - 1; ++i)
	{
		int min = i;
		for(int j = i + 1; j < len; ++j)
		{
			//寻找最小元素下标
			if(arr[j] <= arr[min]) 
			{
				min = j;
			}
			//元素交换
			if(min != i)
			{
				int tmp = arr[i];
				arr[i] = arr[min];
				arr[min] = tmp;
			}
		}
	}
}

 效率分析：时间复杂度为O(n2)，因为每次都要找到最小元素，所以即使在顺序情况下时间复杂度也为O(n2)。

由于在直接选择排序中存在着不相邻元素之间的互换，因此，直接选择排序是一种不稳定的排序方法。

---

 

 堆排序：

       堆的定义： n个元素的序列 { k1， k2 ，…… ， kn }，当且仅当满足k(i) <= k(2*i) && k(i)<=k(2*i+1) 或 k(i) >= k(2*i) && k(i) >= k(2*i+1)称之为堆。（即父节点都大于或小于子结点）

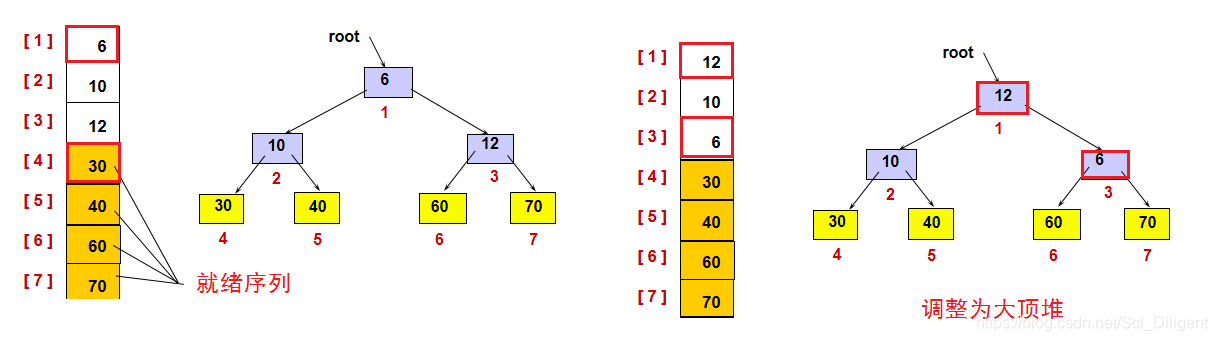
       二叉树的所有根结点值小于或等于左右孩子的值称为小顶堆；二叉树的所有根结点值大于或等于左右孩子的值称为大顶堆。

      基本思想：

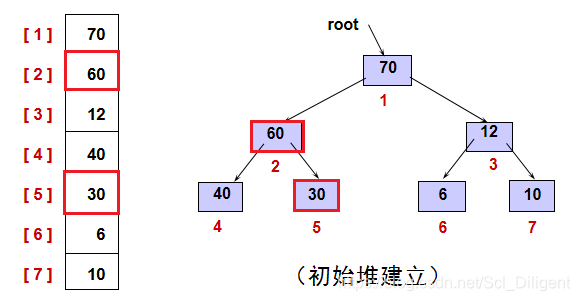
（1）建初始堆： 

将排序码k1，k2，k3，…，kn表示成一棵完全二叉树，然后从第 n/2个排序码(即树的最后一个非终端结点)开始筛选，使由该结点作根结点组成的子二叉树符合堆的定义，然后从第 n/2-1 个排序码重复刚才操作，直到第一个排序码止。这时候，该二叉树符合堆的定义，初始堆已经建立。

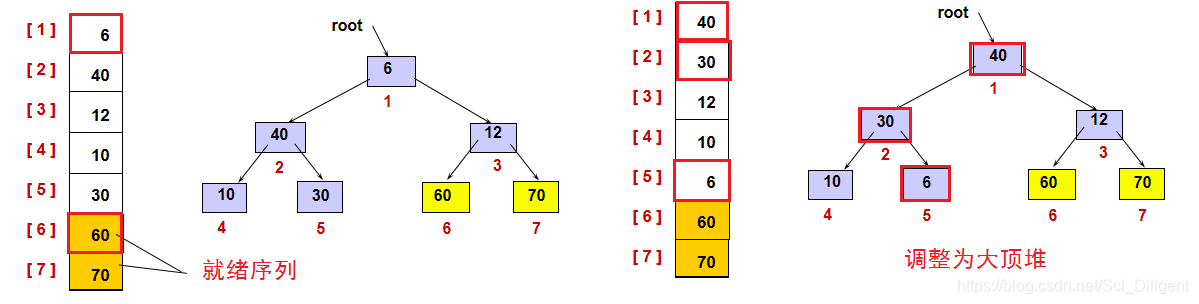
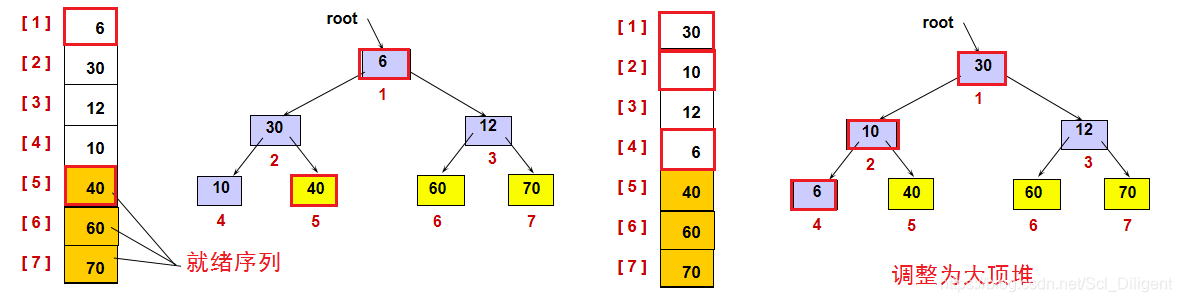
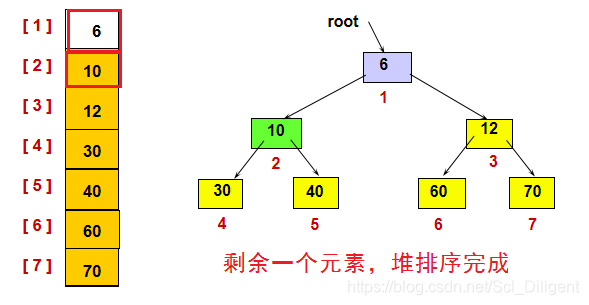
（2）堆排序：

将堆中第一个结点（二叉树根结点）和最后一个结点的数据进行交换（k1与kn），再将k1~kn-1重新建堆，然后k1和kn-1交换，再将k1~kn-2重新建堆，然后k1和kn-2交换，如此重复下去，每次重新建堆的元素个数不断减1，直到重新建堆的元素个数仅剩一个为止。这时堆排序已经完成，则排序码k1，k2，k3，…，kn已排成一个有序序列。

 

 

void HeapAdjust(int* arr, int root, int len)
{
	int  i = root;
	int tmp = 0;
	for(int j = 2 * i + 1; j < len ; j = 2 * i + 1)
	{
		//寻找左右孩子中的较大一个
		if(j < len -1 && arr[j + 1] > arr[j] )
		{
			++j;//右孩子
		}

		//大孩子小于父节点，不交换
		if(arr[j] < arr[i])
			break;

		//大孩子大于父节点，交换
		if(arr[i] < arr[j])
		{
			tmp = arr[i];
			arr[i] = arr[j];
			arr[j] = tmp;

			i = j;//以孩子结点为根节点，再进行调整
		}
	}
}

void HeapSort(int* arr, int len)
{
	//初始大顶堆，最后一个非终端结点至根节点，进行反复筛选
	for(int i = len / 2 -1; i >= 0; --i)
	{
		HeapAdjust(arr, i, len);
	}

	//将第1个到第i-1个元素调整成一个堆
	int tmp = 0;
	for(int i = len - 1; i > 0; --i)
	{
		//将堆顶元素和最后元素交换，待排序列长度-1
		tmp = arr[i] ;
		arr[i] = arr[0];
		arr[0] = tmp;

		HeapAdjust(arr, 0, i); //调整新堆
	}
}

堆排序效率分析：

在整个堆排序中，共需要进行（n/2）+ n -1次筛选运算，每次筛选运算进行双亲和孩子或兄弟结点的排序码的比较和移动次数都不会超过完全二叉树的深度（log2n）+1 ，所以，每次筛选运算的时间复杂度为O(log2n)，故整个堆排序过程的时间复杂度为O(nlog2n)。

堆排序占用的辅助空间为1（供交换元素用），故它的空间复杂度为O（1）。

堆排序是一种不稳定的排序方法。