深度学习_用LSTM+Attention与Self-Attention

笔者在重新尝试用深度学习的各个模型对序列进行预测，就LSTM进行一些使用记录

一、一些优化

1. 和keras一样的权重初始化
   • 有时候我们torch训练的LSTM， 没有keras好，可以将权重按keras的方式进行初始化
2. 增加attention 捕捉序列的周期与相似性
3. 尝试用self-attention

二、网络结构LSTM+Attention

import torch
from torch import nn
import torch.nn.functional as F
from torch.utils.data import DataLoader, TensorDataset
import typing as typ
import numpy as np
from tqdm import tqdm
from sklearn.model_selection import KFold
from collections import OrderedDict


class LSTMRegressor(nn.Module):
    def __init__(self, input_size, hidden_size=128):
        super(LSTMRegressor, self).__init__()
        self.lstm = nn.LSTM(input_size, hidden_size, batch_first=True, bidirectional=False)
        self.header = nn.Sequential(OrderedDict([
            ('fc1', nn.Linear(hidden_size, 32)),
            ('relu1', nn.ReLU(inplace=True)),
            ('dropout', nn.Dropout(0.01)),
            ('fc2', nn.Linear(32, 1)),
            ('relu2', nn.ReLU(inplace=True)),
        ]))
        self.__weight_init()
        # attention
        self.attn_ly = nn.Linear(hidden_size, 1)
        self.sft = nn.Softmax(dim=1)

    def attention_net(self, lstm_output):   
        # print('lstm_output', lstm_output.shape) # batch_size, time_step, hidden_size * layer_size
        attn_tanh = torch.tanh(self.attn_ly(lstm_output))  # batch_size, time_step, 1
        sft_res = self.sft(attn_tanh) # batch_size, time_step, 1
        attn_output = torch.sum(sft_res * lstm_output, 1) # batch_size, hidden_size
        return attn_output

    def forward(self, x):
        x_out, (hn, cn) = self.lstm(x)
        x_out = self.attention_net(x_out)
        x_out = self.header(x_out)
        return x_out

    def __weight_init(self):
        """
        Tensorflow/Keras-like initialization
        """
        for name, p in self.named_parameters():
            if 'lstm' in name:
                if 'weight_ih' in name:
                    nn.init.xavier_uniform_(p.data)
                elif 'weight_hh' in name:
                    nn.init.orthogonal_(p.data)
                elif 'bias_ih' in name:
                    p.data.fill_(0)
                    # Set forget-gate bias to 1
                    n = p.size(0)
                    p.data[(n // 4):(n // 2)].fill_(1)
                elif 'bias_hh' in name:
                    p.data.fill_(0)
            elif 'fc' in name:
                if 'weight' in name:
                    nn.init.xavier_uniform_(p.data)
                elif 'bias' in name:
                    p.data.fill_(0)

三、Self-attention

3.1 原理

考虑全部序列

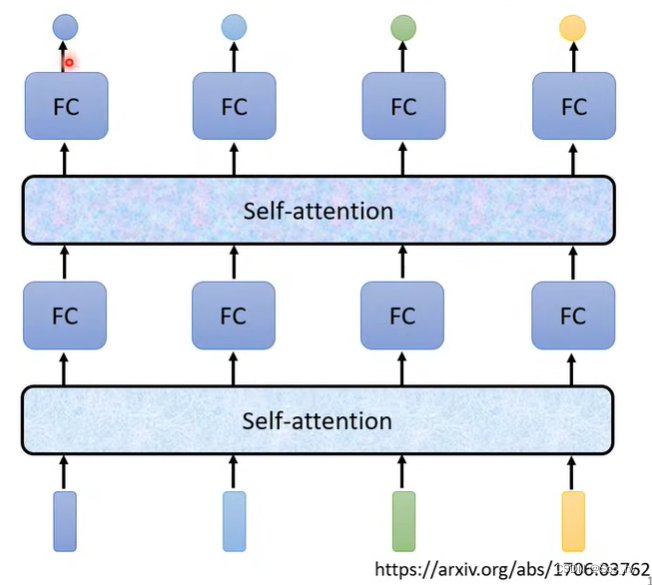
计算序列中元素之间的关系$\alpha$， 存在较多的方法进行计算，一种是直接进行乘积Dot-product，一种是concat后做一个激活函数。在self-attention中使用的是左边的进行乘积Dot-product的方法。

以序列第一个值为例，输入$q_1={\mathbf{W}}^{\mathbf{q}}{\mathbf{a}}^1$， 计算每个值和第一个值之间的相关性（用k矩阵抽取核心${\mathbf{K}}^2={\mathbf{W}}^2{\mathbf{a}}^2;$ 然后与q矩阵相乘${\alpha }_{1,2}={\mathbf{K}}^2{\mathbf{q}}_1$），抽取出相关性后，用soft-max进行归一化，增大值之间的距离。

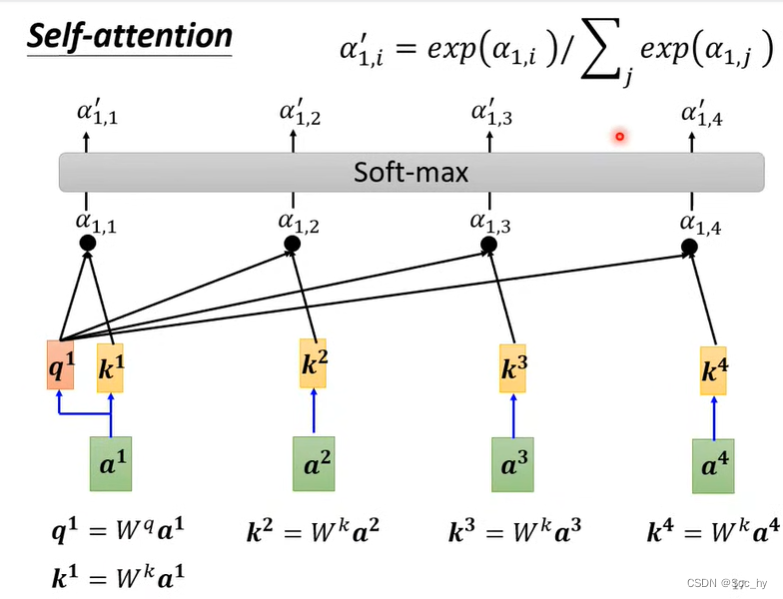
有了相关性之后对每个值(${\mathbf{v}}^2={\mathbf{W}}^{\mathbf{v}}{\mathbf{a}}^2$)都取相应相关性(${\mathbf{v}}^2{\alpha }_{1,2}^{/}$)的特征做累和
($b^1={\sum }_i{\alpha }_{1,i}^{/}{\mathbf{v}}^{\mathbf{i}}$)
然后依次的获取$b^2{b}^3{b}^4$

3.2 原理转矩阵乘法

$a^i$合并成矩阵$I$，所以

• $K^i$ 可以合并成 $K=W^{k}I$
• $q^i$ 可以合并成 $Q=W^{q}I$
• $v^i$ 可以合并成 $V=W^{q}I$
• ${\alpha }_{i,j}$ 可以合并成$A=K^{T}Q$
• ${\alpha }_{i,j}^{/}$ 可以转换成$A^{/}$
• $b^i$ 最终的输出可以转换成$O=V{A}^{/}$

所以未知参数仅仅$W^k{W}^q{W}^v$

3.3 Multi-head self-attention

其实就是多个q去找相关性。

• $q^i$ -> $Q=W^{q}I$
  • 分别用矩阵乘$Q$以得到两个Q
  • $Q^1=W^{q.1}Q$
  • $Q^2=W^{q,2}Q$
• $K^i$ -> $K=W^{k}I$
  • 分别用矩阵乘$K$以得到两个K
  • $K^1=W^{k.1}K$
  • $K^2=W^{k,2}K$
• $V^i$ -> $V=W^{v}I$
  • 分别用矩阵乘$V$以得到两个V
  • $V^1=W^{v.1}V$
  • $V^2=W^{v,2}V$
• 算出两个O
  • $A_1^{/}=softmax({K^1}^T{Q}^1)O^1=V^1{A^1}^{/}$
  • $A_2^{/}=softmax({K^2}^T{Q}^2)O^2=V^2{A^2}^{/}$
• 然后concat在一起
  • $O=W^{O}concat(O^1,O^2)$

3.4 位置的Encoding

因为前面attention并没有考虑位置的信息，所以可以加入位置的信息

• 在输入中加入到位置信息$e^i$
  • $e^i+a^i$
• 原始论文使用的是 $concat(sin(idx),cos(idx))$