368. 最大整除子集

给出一个由无重复的正整数组成的集合，找出其中最大的整除子集，子集中任意一对 (Si，Sj) 都要满足：Si % Sj = 0 或 Sj % Si = 0。

如果有多个目标子集，返回其中任何一个均可。

 

示例 1:

输入: [1,2,3]
输出: [1,2] (当然, [1,3] 也正确)

示例 2:

输入: [1,2,4,8]
输出: [1,2,4,8]

思路：较小数对较大数取余一定为0，那么问题就变成了看较大数能不能整除这个较小数。如果数组是无序的，处理起来就比较麻烦，所以我们首先可以先给数组排序，这样我们每次就只要看后面的数字能否整除前面的数字。动态规划解决，额外设置两个数组。

1、其中dp[i]表示到数字nums[i]位置最大可整除的子集合的长度。如何求dp[i]？

对于i，遍历到数组末尾，如果nums[j]能整除nums[i], 且dp[i] < dp[j] + 1的话，本来数字nums[j]位置最大可整除的子集合的长度为dp[j]，而此时nums[j]能整除nums[i]，因此，状态转移方程为：dp[i] =max(dp[i] , dp[j] + 1)(j>i).因为同一个数可能存在于好几个整除子集中，所以我们要遍历找最大的。

通过这个过程能看出，求dp[i]需要从后往前遍历，因为求前面的值要用到后面的结果。

2、由于本文需要求出集合的元素，而不仅仅是个数，因此需要第二个数组parents，其中parents[i]存取得最大可整除的子集合的前提下，上一个能整除nums[i]的数字的位置，也就是1中提到的j。最后可以根据parents[i]一点点恢复最大可整除的子集合的元素。

3、两个整型变量mx和mx_idx分别表示最大子集合的长度和起始数字的位置。最后通过mx_idx找到最大可整除的子集合的第一个元素，通过parents[i]顺次找下去，一共找mx个元素，就构成结果了。

因此，总结一下：我们可以从后往前遍历数组，对于某个数字再遍历到末尾，在这个过程中，如果nums[j]能整除nums[i], 且dp[i] < dp[j] + 1的话，更新dp[i]和parent[i]，如果dp[i]大于mx了，还要更新mx和mx_idx。

最后循环结束后，我们来填res数字，根据parent数组来找到每一个数字。

举例如下：

 

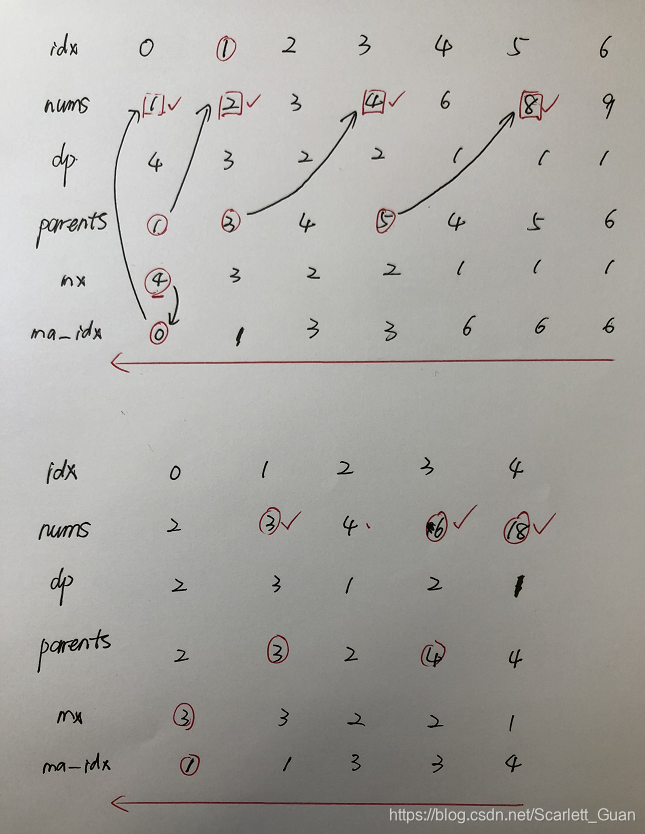
class Solution {
public:
    vector<int> largestDivisibleSubset(vector<int>& nums) {
        sort(nums.begin(), nums.end());
        vector<int>dp(nums.size(), 0), parents(nums.size(), 0), re;
        int mx=0, ma_idx=0;
        for(int i=nums.size()-1; i>=0; --i){
            for(int j=i; j<nums.size(); ++j){//因为同一个数可能存在于好几个整除子集中，所以我们要遍历找最大的
                if(nums[j]%nums[i]==0 && dp[i]<dp[j]+1){
                    dp[i]=dp[j]+1;
                    parents[i]=j;
                }
            }
            if(dp[i]>mx){
                mx=dp[i];
                ma_idx=i;
            }
        }
        //回溯找到最大的整除子集
        for(int i=0; i<mx; ++i){
            re.push_back(nums[ma_idx]);
            ma_idx=parents[ma_idx];
        }
        return re;
    }
};