CSP-J 初赛模拟卷8（CSP-J2021真题）题解

原创已于 2023-08-26 09:48:51 修改 · 1.5k 阅读

10 ·

CC 4.0 BY-SA版权

文章标签：

#算法

于 2023-08-25 15:11:19 首次发布

得分：71

注：这套原题只有答案没有题解，题解是我自己写的，如有错误或需改正的地方请大佬详解

1.以下不属于面向对象程序设计语言的是（D）。
A. C++
B. Python
C. Java
D. C

题解：傻瓜题，不讲了

知识点总结：C语言属于面向过程的语言，C++、python、java等属于面向对象的语言

2.以下奖项与计算机领域最相关的是（B）。
A. 奥斯卡奖
B. 图灵奖
C. 诺贝尔奖
D. 普利策奖

题解：傻瓜题，只有图灵这个人与计算机相关

知识点总结：图灵奖是计算机领域的最高奖项

3. 目前主流的计算机储存数据最终都是转换成（A）数据进行存储。
A. 二进制
B. 十进制
C. 八进制
D. 十六进制

题解：傻瓜题，不讲了

知识点总结：计算机都是把数据以二进制码进行存储的

4. 以比较作为基本运算，在 N 个数中找出最大数，最坏情况下所需要的最少的比较次数
为（C）。
A. N^2
B. N
C. N-1
D. N+1

题解：求最大值可以定义一个max变量，然后循环遍历这n个数，如果第i (1<=i<=n或0<=i<=n-1) 个数的值比max大，那么更新max。最后循环结束输出max，就是最大值。所以时间复杂度为O(n)

知识点总结：题干就是

5. 对于入栈顺序为 a,b,c,d,e 的序列，下列（D）不是合法的出栈序列。
A. a,b,c,d,e
B. e,d,c,b,a
C. b,a,c,d,e
D. c,d,a,e,b

题解：傻瓜题，不讲了

6. 对于有 n 个顶点，m 条边的无向连通图（m>n），需要删掉（D）条边才能使其称为一棵
树。
A. n-1
B. m-n
C. m-n-1
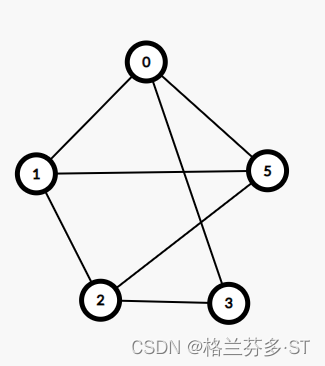
D. m-n+1

题解：这是图的一个性质。如果不知道，也可以把m和n设为一个具体的数来计算找规律，比如说下面这个图：

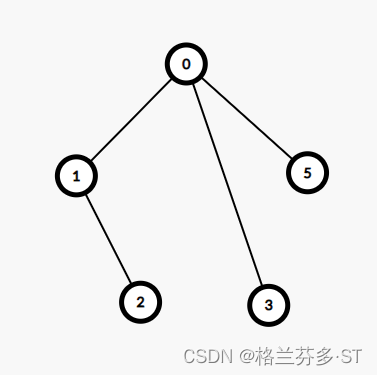
要想使它变成一棵树，（我不小心把4漏了）就需要把1和5之间、2和3之间、2和5之间的3条边删除，这个图就变成这样：

这样，这个图就变成了一棵树，这个图有5个顶点和7条边，则7-5+1=3条边

知识点总结：题干就是

7. 二进制数 101.11 对应的十进制数是（C）
A. 6.5
B. 5.5
C. 5.75
D. 5.25

题解：傻瓜题，不讲了

8. 如果一棵二叉树只有根结点，那么这棵二叉树高度为 1。请问高度为 5 的完全二叉树有
（A）种不同的形态？
A. 16
B. 15
C. 17
D. 32

题解：完全二叉树是每一层的结点必须从左到右排列，第五层共有16个节点，则此完全二叉树共有16种不同的形态

知识点总结：高度为n的完全二叉树有2^(n-1)个结点

9. 表达式 a*(b+c)*d 的后缀表达式为（B），其中“*”和“+”是运算符。
A. **a+bcd
B. abc+*d*
C. abc+d**
D. *a*+bcd

题解：中缀转后缀的两种最简单的方法（栈我觉得比较麻烦）都可以做：

（1）先按照优先级给每个单项式添上括号，再把运算符移到单项式之后，最后去掉所有的括号：a*(b+c)*d →((a*(b+c))*d) → ((a(bc)+)*d)* → abc+*d*

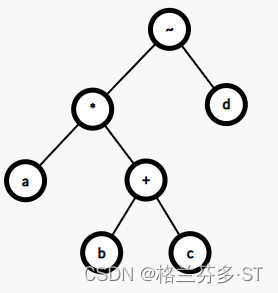
（2）生成如下的二叉树，然后后序遍历即可：（这个画树软件两个结点不能重名，所以第二个乘号用~代替，请谅解）

知识点总结：中缀表达式转前（后）缀表达式的方法：

（1）生成二叉树，然后前（后）序遍历即可

（2）按照优先级给每个单项式都添上括号，然后把运算符移到数字前面，最后去掉所有的括号

（3）符号栈。遇到数字直接输出，符号必须进栈。如果符号入栈时栈顶符号优先级大于等于将入栈符号，栈顶直接出栈，否则将入栈符号入栈。遇到左括号直接入栈，遇到右括号则把栈内元素出栈，直至左括号出栈

10. 6 个人，两个人组一队，总共组成三队，不区分队伍的编号，不同的组队情况有

（C B）种。
A. 10
B. 15
C. 30
D. 20

错解：C

正解：B

错因分析：最后忘了除以A(3,3)了

正解题解：首先从6个人里选出两个人分到第一队，再从4个人中选出两个人分到第二队，但是这是考虑队伍编号，所以还要除以A(3,3)，则总共的组队情况有C(2,6)×C(2,4)÷A(3,3)=15种

11. 在数据压缩编码种的哈夫曼编码方法，在本质是一种（B）的策略。
A. 枚举
B. 贪心
C. 递归
D. 动态规划

题解：哈夫曼编码是每次选根结点最小的两棵树，所以是贪心

知识点总结：哈夫曼编码本质上是贪心的策略

12. 由 1，1，2，2，3 这五个数字组成不同的三位数有（A）种。
A. 18
B. 15
C. 12
D. 24

题解：分类枚举，先计算出有两个1一个2的数字个数，再计算有两个2一个1的数字个数，然后计算有两个2一个3的数字个数，再然后计算有两个1一个3的数字个数，最后计算123都有的数字个数。则前四种每一种的全部情况数均为3种，最后一种的情况数是3的全排列=6种。则总情况数=3×4+6=18种

13. 考虑如下递归算法
solve(n)
if n<=1 return 1
else if n>=5 return n*solve(n-2)
else return n*solve(n-1)
则调用 solve(7)得到的返回结果为（C）。
A. 105
B. 840
C. 210
D. 420

题解：傻瓜题。注意不要算错，递归计算量较大

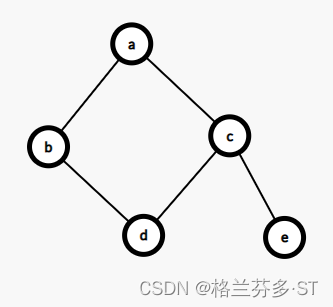
14. 以 a 为起点，对右边的无向图进行深度优先遍历，则 b,c,d,e 四个点中有可能作为最后
一个遍历到的点的个数为（B）。

A. 1
B. 2
C. 3
D. 4

题解：对这个图进行DFS，共有两条最优路线：abdce和acedb。首先查找起点a的邻接点，分别为b和c，b除a以外的邻接点只有d，因为d不是a的邻接点，所以d不可能是最后遍历到的点；c还有两个邻接点d和e，已知d不可能是最后遍历到的，那么查找e除c以外的的邻接点，发现不存在这样的一个点，故e可以最后一个遍历到。则总共有两个点可以最后遍历到

15. 有四个人要从 A 点坐一条船过河到 B 点，船一开始在 A 点。该船一次最多可坐两个
人。已知这四个人中每个人独自坐船的过河时间分别为 1，2，4，8，且两个人坐船的过河
时间为两人独自过河时间的较大者。则最短（B）时间可以让四个人过河到 B 点（包括从 B
点把船开回 A 点的时间）。
A. 14
B. 15
C. 16
D. 17

题解：用贪心的思想很容易：

设过河时间由快到慢排序，四个人的编号分别为ABCD。

两种优选策略（选最优的一种）：
（1）最快和最慢过去，最快回；最快和次慢过去，最快回；
（2）最快和次快过去，最快回；最慢和次慢过去，次快回。

经过比较，发现按照优选策略1所需时间：

8+1+4+1+2=16

按照优选策略2所需时间：

2+1+8+2+2=15

优选策略2所需时间较少

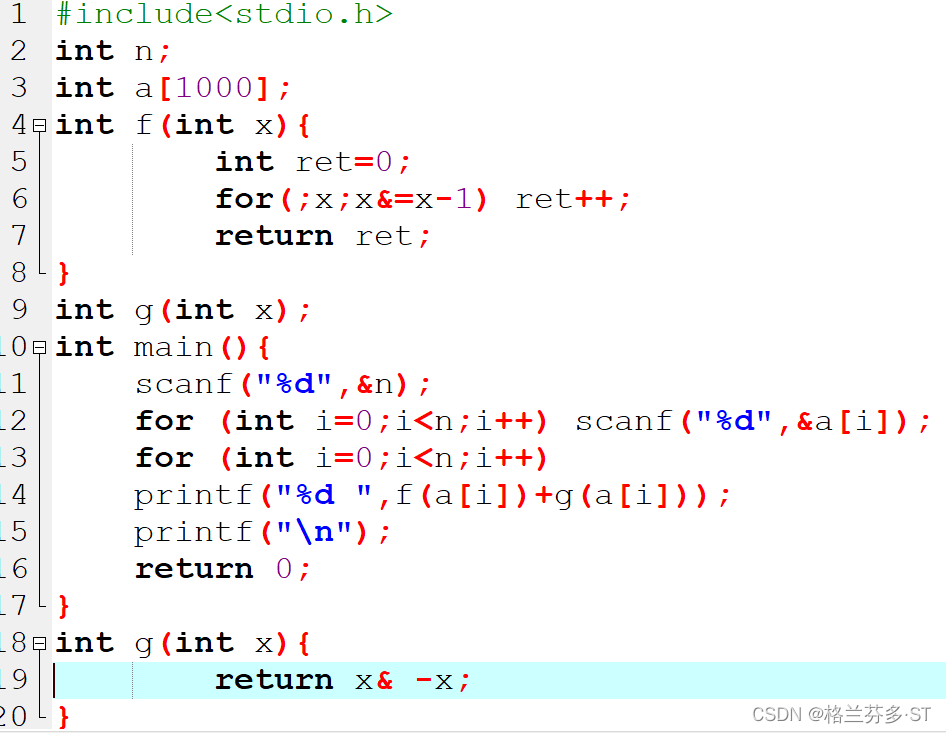
16. 阅读程序（程序输入不超过数组或字符串定义的范围，共计 40 分）
#include <stdio.h>

int n;
int a[1000];

int f(int x)
{
        int ret = 0;
        for(; x; x &= x - 1) ret ++;
        return ret;
}

int g(int x)
 {
        return x & - x;
}

int main()
 {
        scanf("%d", &n);
        for (int i = 0; i < n; i++) scanf("%d", &a[i]);
        for (int i = 0; i < n; i++)
        printf("%d ", f(a[i]) + g(a[i]));
        printf("\n");
        return 0;
}
输入的 n 等于 1001 时，程序不会发生下标越界。这句话描述是否正确？A B
A.正确
B.错误

17.【单选】1.5 分
输入的 a[i]必须全为正整数，否则程序将陷入死循环。这句话的描述是否正确？B
A.正确
B.错误

18.【单选】1.5 分
当输入为“5 2 11 9 16 10”时，输出为“3 4 3 17 5”。这句话的描述是否正确？B
A.正确
B.错误

19.【单选】1.5 分
当输入为“1 511998”时，输出为“18”。这句话的描述是否正确？A
A.正确
B.错误

20.【单选】1.5 分
将源代码中 g 函数的定义（13-16 行）移到 main 函数的后面，程序可以正常编译运行。这
句话的描述是否正确？B
A.正确
B.错误

21.【单选】3 分
当输入为“2 -65536 2147483647”时，输出为（B）
A."65532 33"
B."65552 32"
C."65535 34"
D."65554 33"

错因分析：第一题把“不会”看成“会”了

正解题解：
（1）a数组只开了1000个，下标表示范围只有0~999。输入1001下标即使从0开始，a[1000]也属于越界访问

（2）输入小数或字符只会直接退出或输出全0，不会死循环，比如：

（3）（4）（6）代入计算即可

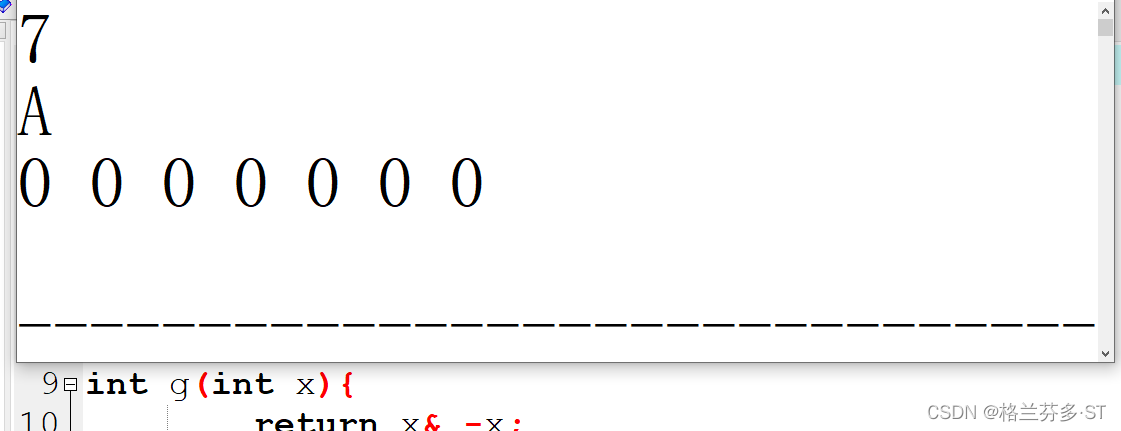
（5）在main函数中调用非库函数，函数必须先声明才能调用，如果函数体写在了main函数之后，那么必须先声明函数类型、函数名和参数才行，不能加大括号。如果把g函数直接移到main函数之后：

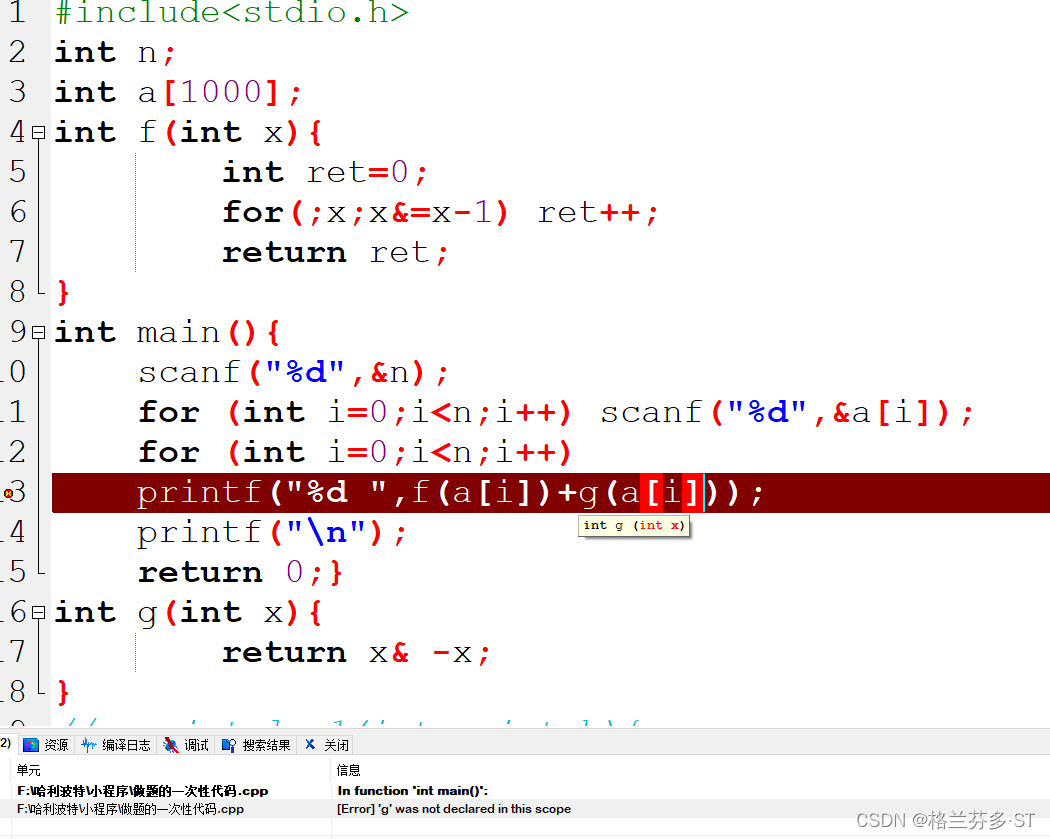
此处程序报错：“[Error] 'g' was not declared in this scope”意思是名叫g的变量或函数未定义，如果改成这样：

编译结果：

这样就通过编译了

22.【单选】1.5 分
#include <stdio.h>
#include <string.h>

char base[64];
char table[256];
char str[256];
char ans[256];

void init()
{
        for (int i = 0; i < 26; i++) base[i] = 'A' + i;
        for (int i = 0; i < 26; i++) base[26 + i] = 'a' + i;
        for (int i = 0; i < 10; i++) base[52 + i] = '0' + i;
        base[62] = '+', base[63] = '/';

        for (int i = 0; i < 256; i++) table[i] = 0xff;
        for (int i = 0; i < 64; i++) table[base[i]] = i;
        table['='] = 0;
}

void decode(char *str)
{
        char *ret = ans;
        int i, len = strlen(str);
        for (i = 0; i < len; i += 4){
                (*ret++) = table[str[i]] << 2 | table[str[i + 1]] >> 4;
                if(str[i + 2] != '=')
                (*ret++) = (table[str[i + 1]] & 0x0f) << 4 | table[str[i + 2]] >> 2;
                if(str[i + 3] != '=')
                (*ret++) = table[str[i + 2]] << 6 | table[str[i + 3]];
}
}

int main()
 {
        init();
        printf("%d\n", (int)table[0]);

        scanf("%s", str);
        decode(str);
        printf("%s\n", ans);
        return 0;
}
输出的第二行一定是由小写字母、大写字母、数字和“+”、“/”、“=”构成的字符串。这句话的
描述是否正确？A B
A.正确
B.错误

23.【单选】1.5 分
可能存在输入不同，但输出的第二行相同的情形。这句话的描述是否正确？A
A.正确
B.错误

24.【单选】1.5 分
输出的第一行为“-1”。这句话的描述是否正确？A
A.正确
B.错误

25.【单选】3 分
设输入字符串长度为 n，decode 函数的时间复杂度为（B）
A.O(√n)
B.O(n)
C.O(nlogn)
D.O(n^2)

26.【单选】3 分
当输入为“Y3Nx”时，输出的第二行为（C B）
A.“csp”
B.“csq”
C.“CSP”
D.“Csp”

27.【单选】3.5 分
当输入为“Y2NmIDIwMjE=”时，输出的第二行为（A C）
A.“ccf2021”
B.“ccf2022”
C.“ccf 2021”
D.“ccf 2022”

错因分析：这个算法好像是base64（可以理解为六十四进制），所以直接按照base64的规则答得题，最后两题算错了

正解题解：

（1）也可以出现其他字符，不信你试试（不过因为ans数组被table数组赋值，而table数组提前全部初始化为255 (0xff) ，所以有时会输出乱码

（2）中间如果有换行符，可以使输入相同，输出第二行不同。

（3）因为ans数组被table数组赋值，而table数组提前全部初始化为255 (0xff) ，此处用8位二进制存储，255的二进制本来是1111 1111，但是最高位是符号位，所以这个数再转回8位二进制就是-1

（4）decode函数中，循环从0到字符串的长度，也就是题目设的n。不用管后面的i到底每次怎么变化，近似时间复杂度是O(n)

（5）

代入计算即可
Y3Nx 每个字符对应6个比特位、
Y=24=011 000
3=55=110 111
N=13=001 101
x=49=110 001

把数据拼接并重新编码：
01100011 01110011 01110001
99->c 115->s 113->q

（6）同第五题

28.【单选】1.5 分
#include<stdio.h>

#define n 100000
#define N n + 1

int m;
int a[N],b[N],c[N],d[N];
int f[N],g[N];

void init()
{
        f[1] = g[1] = 1;
        for(int i = 2;i <= n;i++){
        if(!a[i]) {
                b[m++] = i;
                c[i] = 1,f[i] = 2;
                d[i] = 1,g[i] = i + 1;
        }
        for(int j = 0;j < m && b[j] * i <= n;j++){
                int k = b[j];
                a[i * k] = 1;
                        if(i * k == 0){
                                c[i * k] = c[i] + 1;
                                f[i * k] = f[i] / c[i * k] * (c[i * k] + 1);
                                d[i * k] = d[i];
                                g[i * k] = g[i] * k + d[i];
                                break;
                        }
                        else{
                                c[i * k] = 1;
                                f[i * k] = 2 * f[i];
                                d[i * k] = g[i];
                                g[i * k] = g[i] * (k + 1);
                        }
                }
        }
}

int main()
{
        init();

        int x;
        scanf("%d",&x);
        printf("%d %d\n",f[x],g[x]);
        return 0;
}
若输入不为“1”，把第 12 行删去不会影响输出的结果。这句话的描述是否正确？B A
A.正确
B.错误

29.【单选】2 分
第 24 行的“f[i] / c[i * k]”可能存在无法整除而向下取整的情况。这句话的描述是否正确？A B
A.正确
B.错误

30.【单选】2 分
在执行完 init()后，f 数组不是单调递增的，但 g 数组是单调递增的。这句话的描述是否
正确？（B）
A.正确
B.错误

31.【单选】3 分
init 函数的时间复杂度为（D A）。
A.O(n)
B.O(nlogn)
C.O(n√n)
D.O(n^2)

32.【单选】3 分
在执行完 init()后，f[1]，f[2]，f[3] …… f[100]中有（B C）个等于 2。
A.23
B.24
C.25
D.26

33.【单选】4 分
当输入为“1000”时，输出为（C）
A.”15 1340”
B.”15 2340”
C.”16 2340”
D.”16 1340”

错因分析：看着像是欧拉筛代码，但是它多了很多变量。所以我以为它是个新的没接触的算法，不好分析

正解题解：

a数组表示标记数组 a[i]为false，表示i是质数。
b数组表示存储所有质数
f数组表示存储x的因数个数
g数组表示x的所有因数之和（我没搞清这些数组的关系）

（1）循环从2开始，所以不会考虑1

（2）c[i*k]是f[i]的因数，所以不存在不能整除的情况

（3）g数组存储x的所有因数之和，肯定不可能是单调递增的，一个数的因数个数不相同，和也不会是单调递增的；f数组不会是单调递增的，因为因数个数也有多有少，不是单调递增的

（4）欧拉筛时间复杂度为O(n)

（5）因数个数为2的数只可能是质数，100以内共有25个质数

（6）代入计算即可

34.【单选】3 分
完善程序。
（Josephus 问题）有 n 个人围成一个圈，一次标号 0 至 n-1，从 0 号开始，依次 0，1，
0，1，. . . . 交替报数，报道 1 的人会离开，直至圈中只剩下一个人，求最后剩下人的编
号。
试补全模拟程序
#include<stdio.h>

const int MAXN=1000000;
int F[MAXN];

int main(){
    int n;
    scanf("%d",&n);
    int i=0,p=0,c=0;
    while( ① ){
        if(F[i]==0){
            if( ② ){
                F[i]=1;
                ③;
            }
        ④ ;
        }
        ⑤ ;
    }
    int ans=-1;
    for(int i=0;i<n;i++)
        if(F[i]==0)
            ans=i;
    printf("%d\n",ans);
    return 0;
}
①处填（D）
A.i<n
B.c<n
C.i<n-1
D.c<n-1

35.【单选】3 分
②处填（C）
A.i%2==0
B.i%2==1
C.p
D.!p

36.【单选】3 分
③处填（C）
A.i++
B.i=(i+1)%n
C.c++
D.p^=1

37.【单选】3 分
④处填（D）
A.i++
B.i=(i+1)%n
C.c++
D.p^=1

38.【单选】3 分
⑤处填（B）
A.i++
B.i=(i+1)%n
C.c++
D.p^=1

题解：

i是数组下标，c是已经筛掉了多少人，还需要一个变量记录当前这个人报0还是1，就是p。

（1）如果除最后剩下的人的其他所有人都被筛掉，循环结束，所以循环条件是c<n-1

（2）（3）判断p是否等于1。如果等于1计数器c就加一

（4）p每次需要异或1，这样才能交替循环

（5）无论是否被筛掉都需要进行此操作，就是让i从前往后循环的扫描，因为是一个环，所以最后还有个取余操作。

39.【单选】3 分
（矩形计数）平面上有 n 个关键点，求有多少个四条边都和 x 轴或者 y 轴平行的矩
形，满足四个顶点都是关键点。给出的关键点可能有重复，但完全重合的矩形只计一次。
试补全枚举算法。
#include <stdio.h>

struct point{
    int x, y, id;
};

int equals(struct point a,struct point b){
    return a.x == b.x && a.y == b.y;
}

int cmp(struct point a, struct point b){
    return ①;
}

void sort(struct point A[], int n){
    for(int i = 0; i < n; i++)
        for(int j = 1; j < n; j++)
            if(cmp(A[j], A[j - 1])){
                struct point t=A[j];
                A[j] = A[j - 1];
                A[j - 1] = t;
            }
}

int unique(struct point A[],int n){
    int t=0;
    for(int i = 0; i < n; i++)
        if(②)
        A[t++] = A[i];
    return t;
}

int binary_search(struct point A[], int n, int x, int y){
    struct point p;
    p.x = x;
    p.y = y;
    p.id = n;
    int a = 0, b = n - 1;
    while(a < b){
        int mid=③;
        if(④)
            a = mid + 1;
        else
            b = mid;
    }
    return equals(A[a], p);
}

#define MAXN 1000
struct point A[MAXN];

int main(){
    int n;
    scanf("%d",&n);
    for(int i = 0; i < n; i++){
        scanf("%d %d", &A[i].x, &A[i].y);
        A[i].id = i;
    }
    sort(A,n);
    n = unique(A, n);
    int ans = 0;
    for(int i = 0; i < n; i++)
        for(int j = 0; j < n; j++)
            if(⑤&& binary_search(A, n, A[i].x, A[j].y) && binary_search(A, n, A[j].x,
            A[i].y)){
                ans++;
            }
    printf("%d\n", ans);
    return 0;
}
①处应填（D B）
A.a.x != b.x ? a.x < b.x : a.id < b.id
B.a.x != b.x ? a.x < b.x : a.y< b.y
C.equals(a,b) ? a.id<b.id:a.x<b.x
D.equals(a,b) ? a.id<b.id: (a.x != b.x ? a.x < b.x : a.y< b.y)

40.【单选】3 分
②处应填（B D）
A.i == 0 || cmp(A[i], A[i - 1])
B.t == 0 || equals(A[i], A[t - 1])
C.i == 0 || !cmp(A[i], A[i - 1])
D.t == 0 || !equals(A[i], A[t -1])

41.【单选】3 分
③处应填（C）
A.b – (b – a) / 2 + 1
B.(a + b + 1) >> 1
C.(a + b) >> 1
D.a + (b – a + 1) / 2

42.【单选】3 分
④处应填（B）
A.!cmp(A[mid], p)
B.cmp(A[mid], p)
C.cmp(p, A[mid])
D.!cmp(p, A[mid])

43.【单选】3 分
⑤处应填（C D）
A. A[i].x == A[j].x
B.A[i].id < A[j].id
C.A[i].x == A[j].x && A[i].id < A[j].id
D.A[i].x<A[j].x && A[i].y < A[j].y

错因分析：太长了，我尽管分析了，但是还是毫无头绪

正解题解（题解我实在写不出来，抄的人家的，敬请谅解）：
（1）以x为第一关键字,y为第二关键字进行升序排列。
（2）第一个点或者不重复的点，保留下来.
（3）二分查找左边界，不用+1.
（4）A[mid]小于p的情况，故A[mid]在前。
（5）为了避免重复，必须前面的点坐标小于后面的点。