1、卡诺图的构成

卡诺图的排列有一定规律,可以说是真值表的直观图,在保证任意相邻格子只有一个变量不同的情况下,从上到下从左到右依次排列。
2、逻辑函数在卡诺图上的表示
F(A,B,C,D)=∑m(1,2,3,8,9,10,15),表示如下。∑代表每一个格子对应一个最小项,括号里数字是m的下标,对应的格子填上1,其余格子填上0.
F (A,B,C,D) =∏m(0, 4, 5 ,6 ,7 ,11 ,12 , 13, 14)的表示,也是下图,∏代表每一个格子对应一个最大项,对应的格子填上0,其余格子填上1.正好与最小项的情况相反。
当逻辑函数的形式是F(A,B,C,D)=AB+CD的时候,直接用01表示逻辑表达式,再在对应的格子里填上1和0就好了。
3.通过卡诺图化简逻辑函数
假设下面的逻辑值都为 1:
m0 m1 m4 m5 合并后等于非A非C
m0 m1 m8 m9 合并后等于非A非D
m0 m2 m10 m8合并后等于非B非D
m0 m1 m2 m3合并后等于非C非D
一行对应两个变量
两行对应一个变量
例题:
F=∑m(2,4,6,8)
非A非B非C+AB非CD=0
求最简或-与表达式
解:第一步:
画出卡诺图:
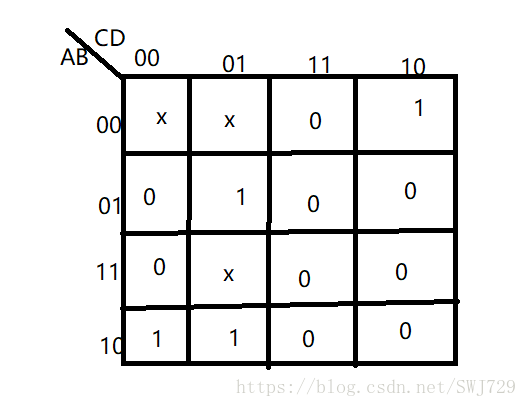
约束项是由最小项组成,约束项为0,每个最小项都为0。
化简时,约束项在卡诺图上的取值,可以根据需要看作0或1。
本题求的时最小项,只需要用卡诺圈圈出0所在的格子就可以了。
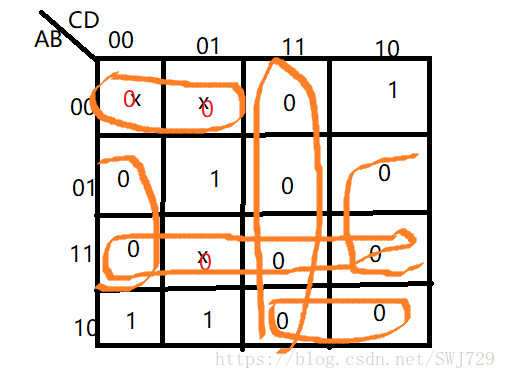





 本文介绍了卡诺图的构成原则,逻辑函数在卡诺图上的表示方式,以及如何通过卡诺图化简逻辑函数。通过实例展示了如何使用卡诺图解决逻辑函数最简表达式的问题。
本文介绍了卡诺图的构成原则,逻辑函数在卡诺图上的表示方式,以及如何通过卡诺图化简逻辑函数。通过实例展示了如何使用卡诺图解决逻辑函数最简表达式的问题。
















 7997
7997

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








