图的深度优先搜索遍历实现

原创已于 2022-03-25 23:46:35 修改 · 2.4k 阅读

4 ·

CC 4.0 BY-SA版权

文章标签：

#c++ #数据结构 #dfs

于 2022-03-25 21:24:53 首次发布

数据结构专栏收录该内容

5 篇文章

订阅专栏

1、题目描述

对图的邻接矩阵和邻接表表示分别进行深度优先搜索遍历算法的实现。

2、设计思路

图的邻接矩阵表示方法中有一个记录各个顶点信息的顶点表和一个表示各个顶点之间关系的邻接矩阵。邻接矩阵中若两个顶点之间没有直接的边相连，则置为∞，否则存储边的信息。对于判断某顶点的度，判断两顶点之间是否有边比较方便，但对于稀疏图的存储尤其浪费空间。
图的邻接表中，同一个顶点发出的边链接在同一个边链表中，每一个链结点代表一条边，边结点中有另一顶点的下标dext和指针link，对于带权图，还要保存该边的权值cost。
无向图的邻接表如下图所示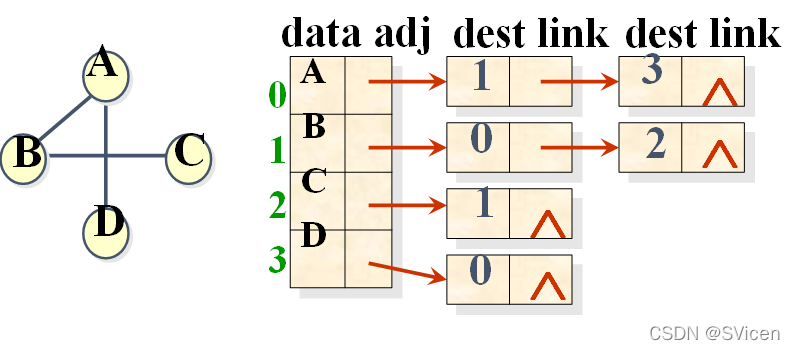： 在这里插入图片描述
邻接矩阵代码实现

#define DefaultVertices 20
#define maxWeight 2147483647    //无穷 
#include<iostream>
using namespace std; 
//邻接矩阵
template <class T, class E>
class Graph1
{
public:
	Graph1(int sz = DefaultVertices);
	~Graph1();
	//插入点
	void addVertices(T v);
	//插入边
	void addEdge(int i, int j, E e);
	//深度优先查找
	void DFSTraverse();
	void DFS(int i);
	friend istream& operator >> (istream& in, Graph1<T, E>& G);   //输入 
	friend ostream& operator << (ostream& out, Graph1<T, E>& G);  //输出 
	//顶点表
	T* VerticesList;        
	//邻接矩阵 
	E** Edge;
	//访问标志数组；
	int* visited;
	//图中最大顶点数 
	int maxVertices;  
	//当前顶点数 
	int numVertices; 
	//当前边数  
	int numEdges;  
	//给出顶点vertex在图中位置 
	int getVertexPos(T vertex)
	{      
		for (int i = 0; i < numVertices; i++)
		{
			if (VerticesList[i] == vertex)
			{
				return i;
			}
		}
		return -1;
	};
};

template <class T, class E>
Graph1<T,E>::Graph1(int sz)
{
	maxVertices = sz;
	numVertices = 0;
	numEdges = 0;
	visited = new int[maxVertices];
	int i, j;
	VerticesList = new T[maxVertices];  //创建顶点表   
	//邻接矩阵    
	Edge = (E**) new E * [maxVertices];
	for (i = 0; i < maxVertices; i++)
	{
		Edge[i] = new E[maxVertices];
	}    
	//矩阵初始化  
	for (i = 0; i < maxVertices; i++)
	{
		for (j = 0; j < maxVertices; j++)
		{
			Edge[i][j] = (i == j) ? 0 : maxWeight;
		}
	}

}

template <class T, class E>
Graph1<T, E>::~Graph1()
{
	delete[] VerticesList;
	for (int i = 0; i < numVertices; i++)
	{
		delete[] Edge[i];
	}
	delete[] Edge;
}

template <class T, class E>
void Graph1<T, E>::addVertices(T v)
{
	VerticesList[numVertices] = v;
	numVertices += 1;
}

template <class T, class E>
void Graph1<T, E>::addEdge(int i, int j, E e)
{
	Edge[i - 1][j - 1] = e;
	Edge[j - 1][i - 1] = e;
	numEdges++;
}

template <class T, class E>
void Graph1<T, E>::DFS(int i)
{
	int j;
	visited[i] = 1;
	cout << VerticesList[i] << " ";
	for ( j = 0; j < numVertices; j++)
	{
		if (Edge[i][j] == 1 && Edge[i][j] != maxWeight && !visited[j])
		{
			DFS(j);
		}
	}
}

template <class T, class E>
void Graph1<T, E>::DFSTraverse()
{
	int i;
	for ( i = 0; i < numVertices; i++)
	{
		visited[i] = 0;
	}
	for ( i = 0; i < numVertices; i++)
	{
		if (!visited[i])
		{
			DFS(i);
		}
	}
}

template <class T, class E>
ostream& operator << (ostream& out, Graph1<T, E>& G)
{
	int i, j;
	out << "节点个数" << G.numVertices << "边个数是：" << G.numEdges << "\n";
	out << "节点为：" << "\n";
	for ( i = 0; i < G.numVertices; i++)
	{
		out << G.VerticesList[i] << " ";
	}
	out << "\n";
	out << "邻接矩阵为：" << "\n";
	for ( i = 0; i < G.numVertices; i++)
	{
		for ( j = 0; j < G.numVertices; j++)
		{
			out << G.Edge[i][j] << " ";
		}
		out << "\n";
	}
	return out;
}
template <class T, class E>
void print(Graph1<T, E>& G)
{
	int i, j;
	cout << "节点个数" << G.numVertices << "边个数是：" << G.numEdges << "\n";
	cout << "节点为：" << "\n";
	for (i = 0; i < G.numVertices; i++)
	{
		cout << G.VerticesList[i] << " ";
	}
	cout << "\n";
	cout << "邻接矩阵为：" << "\n";
	for (i = 0; i < G.numVertices; i++)
	{
		for (j = 0; j < G.numVertices; j++)
		{
			cout << G.Edge[i][j] << " ";
		}
		cout << "\n";
	}
}

int main()
{
	int n = 0;
	Graph1<char, int> G;
	cout << "输入的节点数：";
	cin >> n;
	for (int i = 0; i < n; i++)
	{
		char str;
		cin >> str;
		G.addVertices(str);
	}
	cout << "输入的边数：";
	cin >> n;
	for (int i = 0; i < n; i++)
	{
		int a, b;
		cin >> a >> b;
		G.addEdge(a, b, 1);
	}
	print(G);  //输出邻接矩阵 
	cout<<"DFS搜索顺序：";
	G.DFSTraverse();
	return 0;
}

邻接表代码实现：

#include<iostream>
#define DefaultVertices 20
#define maxWeight 2147483647    //无穷 
using namespace std;
//邻接表
// 定义边表结点
template <class T, class E>
struct ArcNode
{
	int adjvex;// 邻接点域
	E wight;
	ArcNode<T,E>* next;

	ArcNode()
	{
		next = NULL;
	}

	ArcNode(E e,int i, ArcNode<T, E>* n = NULL)
	{
		wight = e;
		adjvex = i;
		next = n;
	}

};
// 定义顶点表结点
template <class T, class E>
struct VertexNode
{
	T data;
	ArcNode<T, E>* firstedge;

	VertexNode()
	{
		firstedge = NULL;
	}
};

template <class T, class E>
class Graph2
{
public:
	Graph2(int sz = DefaultVertices);
	~Graph2();
	//插入点
	void addVertices(T v);
	//插入边
	void addEdge(int i, int j, E e);
	//深度优先查找
	void DFSTraverse();
	void DFS(int i);
	//顶点表
	VertexNode<T,E>* VerticesList;
	//访问标志数组；
	int* visited;
	//图中最大顶点数 
	int maxVertices;
	//当前顶点数 
	int numVertices;
	//当前边数  
	int numEdges;
	//给出顶点vertex在图中位置 
	int getVertexPos(T vertex)
	{
		for (int i = 0; i < numVertices; i++)
		{
			if (VerticesList[i].data == vertex)
			{
				return i;
			}
		}
		return -1;
	};

};

template <class T, class E>
Graph2<T,E>::Graph2(int sz)
{
	maxVertices = sz;
	numVertices = 0;
	numEdges = 0;
	visited = new int[maxVertices];
	VerticesList = new VertexNode<T, E>[maxVertices];  //创建顶点表   

}

template <class T, class E>
Graph2<T, E>::~Graph2(){}

template <class T, class E>
void Graph2<T, E>::addVertices(T v)
{
	VerticesList[numVertices].data = v;
	numVertices++;
}

template <class T, class E>
void  Graph2<T, E>::addEdge(int i, int j, E e)
{
	ArcNode<T, E>* ptredge1 = NULL;
	ptredge1 = VerticesList[i].firstedge;
	while (ptredge1 != NULL)
	{
		ptredge1 = ptredge1->next;
	}
	ptredge1 = new ArcNode<T, E>(e, j);

	ArcNode<T, E>* ptredge2 = NULL;
	ptredge2 = VerticesList[j].firstedge;
	while (ptredge2 != NULL)
	{
		ptredge2 = ptredge2->next;
	}
	ptredge2 = new ArcNode<T, E>(e, i);
	numEdges++;
}

template <class T, class E>
void Graph2<T, E>::DFSTraverse()
{
	int i;
	for ( i = 0; i < numVertices; i++)
	{
		visited[i] = 0;
	}
	for (i = 0; i < numVertices; i++)
	{
		if (!visited[i])
		{
			DFS(i);
		}
	}
}

template <class T, class E>
void Graph2<T, E>::DFS(int i)
{
	ArcNode<T, E>* ptredge = NULL;
	visited[i] = 1;
	cout << VerticesList[i].data << " ";
	ptredge = VerticesList[i].firstedge;
	while (ptredge != NULL)
	{
		if (!visited[ptredge->adjvex])
		{
			DFS(ptredge->adjvex);
		}
		ptredge = ptredge->next;
	}
}

int main()
{
	
	int n = 0;
	Graph2<char, int> G;
	cout << "输入的节点数：";
	cin >> n;
	for (int i = 0; i < n; i++)
	{
		char str;
		cin >> str;
		G.addVertices(str);
	}
	cout << "输入的边数：";
	cin >> n;
	for (int i = 0; i < n; i++)
	{
		int a, b;
		cin >> a >> b;
		G.addEdge(a, b, 1);
	}
	cout << "DFS搜索序列：";
	G.DFSTraverse();
	cout << endl;
	return 0;
}