动态规划-最长公共子序列

最新推荐文章于 2024-04-19 21:11:21 发布

原创最新推荐文章于 2024-04-19 21:11:21 发布 · 359 阅读

8 ·

CC 4.0 BY-SA版权

文章标签：

#动态规划 #算法

文章讲述了如何使用动态规划解决给定两个排列的最长公共子序列问题，通过状态转移方程f[i][j]=max(f[i-1][j],f[i][j-1])或f[i][j]=f[i-1][j-1]+1来计算最长公共子序列的长度。

题目描述

给出 1,2,…,n 的两个排列 P1 和 P2 ，求它们的最长公共子序列。

输入

第一行是一个数 n。

接下来两行，每行为 n 个数，为自然数 1,2,…,n 的一个排列

输出

一个数，即最长公共子序列的长度。

样例输入

3 2 1 4 5

1 2 3 4 5

样例输出

首先,我们先要画一个表格

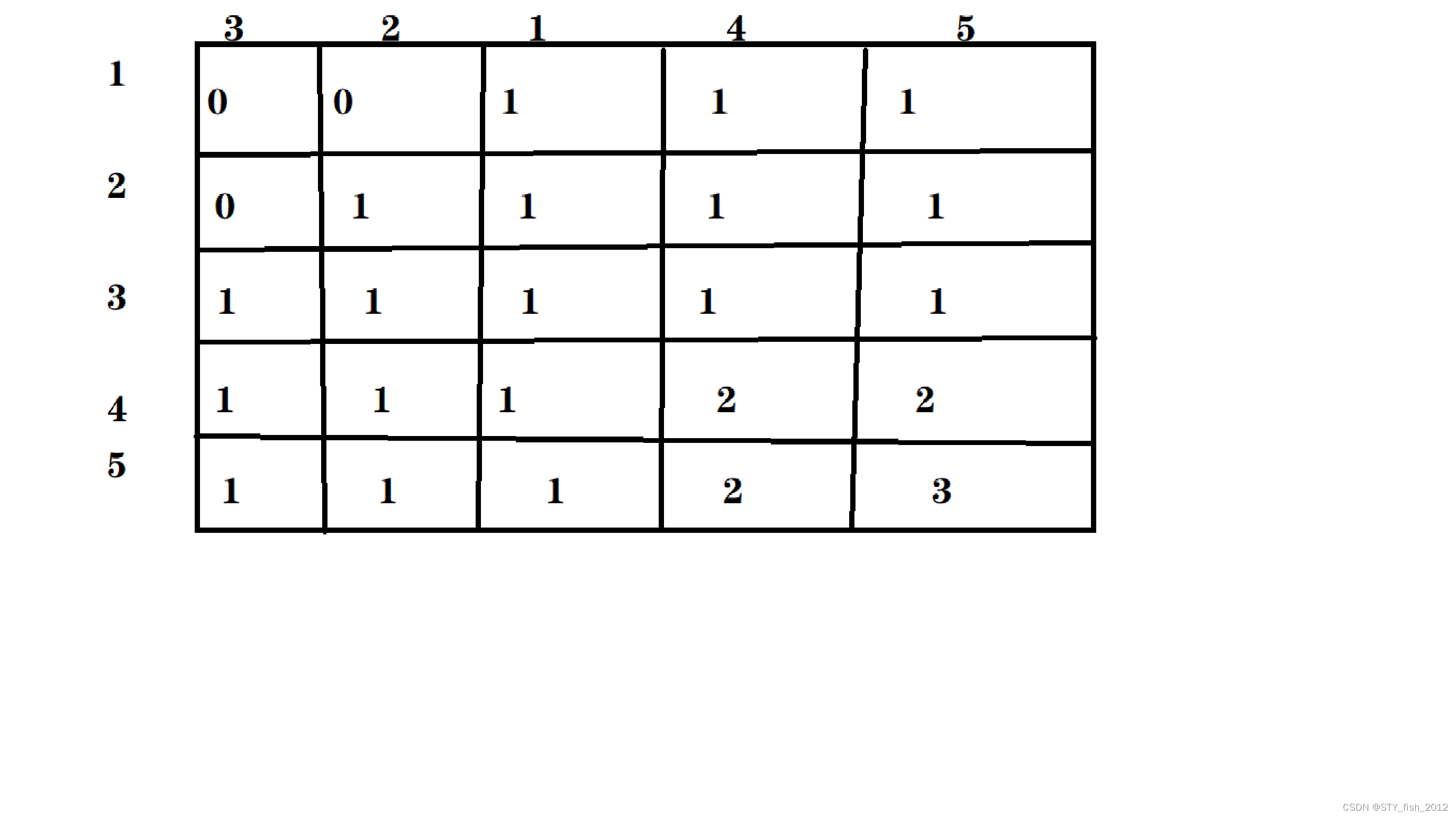
接着,就要找到状态转移方程

我圈出来了几个地方,不难发现,这几个数行号列号都是一样的

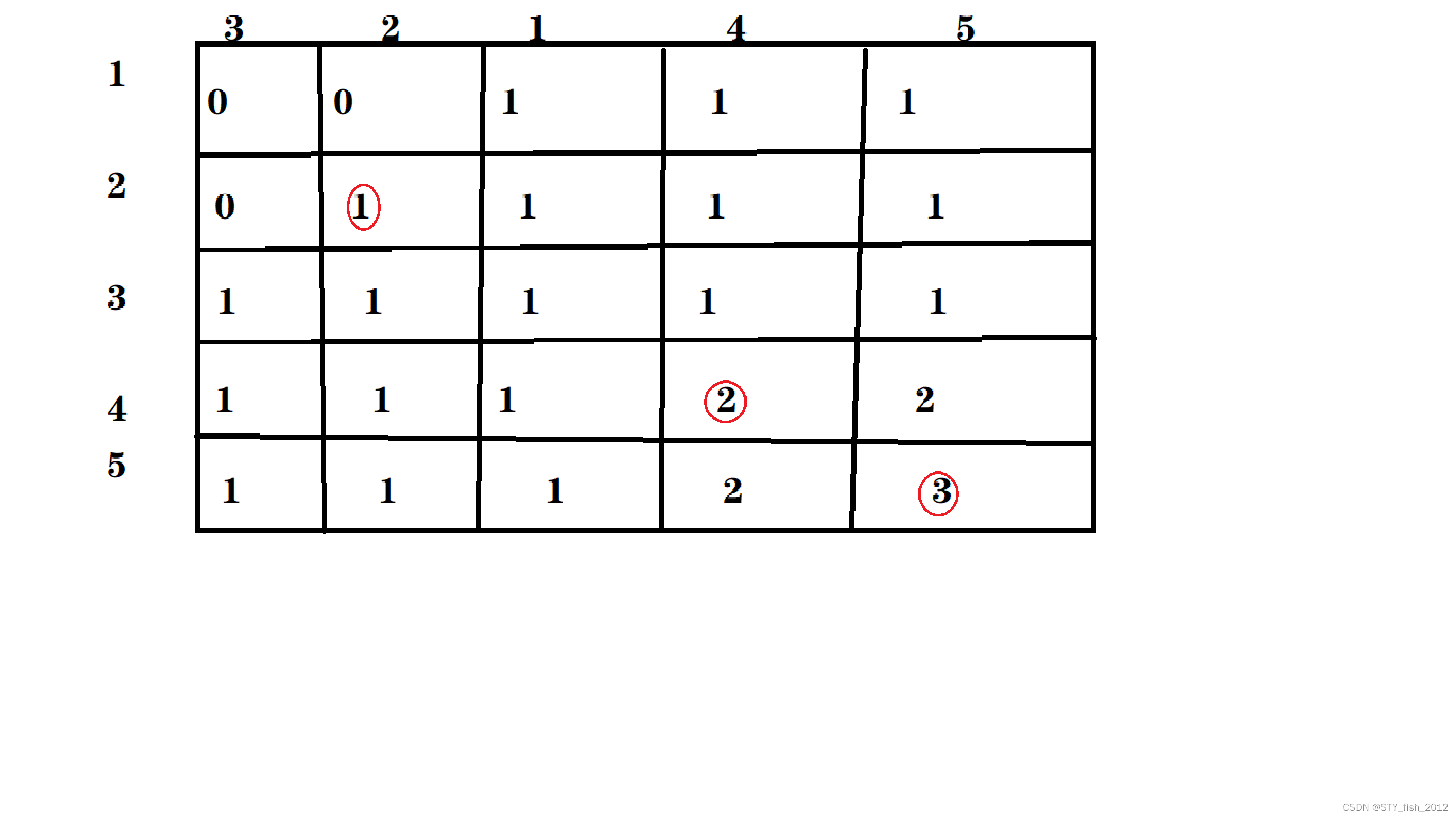
所以可以推出:如果行号的值等于列号,那么这个值就要做改变(在前面的基础上加一)

状态转移方程为

如果行号的值等于列号的值:

f[i][j]=f[i-1][j-1]+1;

否则就继承之前的:

f[i][j]=max(f[i-1][j],f[i][j-1]);

完整代码为:

#include<bits/stdc++.h>
using namespace std;
int n;
int a[5001];
int b[5001];
int f[5001][5001];
int main(){
	cin>>n;
	for(int i=1;i<=n;i++)cin>>a[i];
	for(int i=1;i<=n;i++)cin>>b[i];
	for(int i=1;i<=n;i++)
		for(int j=1;j<=n;j++){
			if(a[i]==b[j])
				f[i][j]=f[i-1][j-1]+1;
			else 
				f[i][j]=max(f[i-1][j],f[i][j-1]);
			}
	cout<<f[n][n];
 	return 0;
}