代码随想录算法训练营第三十二天|动态规划理论基础，509 斐波那契数、70 爬楼梯、746 使用最小花费爬楼梯

 动态规划理论基础

1、动态规划的常见题型（基础类）

• 背包问题（面试常考）
• 打家劫舍
• 股票问题
• 子序列问题

2、动态规划的误区

        注意力全部放在递推公式上，有一种掌握递推公式就可以正确解题的感觉。

        其实，递推公式只是动态规划的一部分，大家稀里糊涂把题目通过了，但其实还是没有掌握动态规划本质性的解题步骤。

3、动态规划的解题步骤（解题时必须要思考清楚的）

（1）动态规划五部曲

• DP数组的含义和下标的含义

        在做题时，有可能就会不清楚DP数组的定义；例如，在子序列问题中，DP数组有可能是二维数组；在背包问题中，有时候也是二维数组(dp[i][j])；那么i表示什么意思，j又表示什么意思；就需要弄清楚

• 递推公式

        递推公式很重要，但也只是动态规划的一部分；大家在做题时就会发现，除了递推公式还有很多重要的步骤需要仔细想清楚。

• DP数组如何初始化

        如果在第一步“DP数组的含义和下标的含义”都没有想清楚，那么这一步大家也是凭借感觉去初始化的；其实，在初始化这里也是很有考究的，在每一道动态规划题目里都涉及到初始化，只是大家没有注意到。

• 遍历顺序

        例如，背包问题在遍历顺序上是非常重要的，反而递推公式非常简单，在01背包里有两层for循环，一个遍历背包，一个遍历物品。那么，为什么是先遍历背包后遍历物品，调换顺序可不可以，为什么是从前到后遍历，从后到前行不行。包括完全背包问题，在求排列和求组合这里，两层for循环是截然不同的遍历顺序。

• 打印DP数组

        有些朋友可能代码和题解代码都差不多了，就是提交通过不了，那么，其实检查问题最直接的方式就是打印DP数组，通过自己对DP数组和下标含义的理解，看看打印出来的数值是不是按照自己的逻辑打印出来的每一个数值。如果，打印的数值和你理解的一样，那就是2-4步中出现了问题，这样思路会更加清晰。如果打印数值和正常结果不一样，那就通过2-4步推导为什么是错误的数值。

（2）五部曲总结

        动态规划五部曲非常重要，如果一道动态规划的题目这五步都思考到位，那么题目就分析的很透彻了，简单题也一定要用这五步，虽然会让题目变得有点复杂，但是这五步是贯彻整个动态规划的，简单题用这五步分析清楚了，难的题依然可以用这五步分析清楚。

一、509 斐波那契数

class Solution {
public:
    int fib(int N) {
        if (N <= 1) return N;
        vector<int> dp(N + 1);
        dp[0] = 0;
        dp[1] = 1;
        for (int i = 2; i <= N; i++) {
            dp[i] = dp[i - 1] + dp[i - 2];
        }
        return dp[N];
    }
};

二、70 爬楼梯

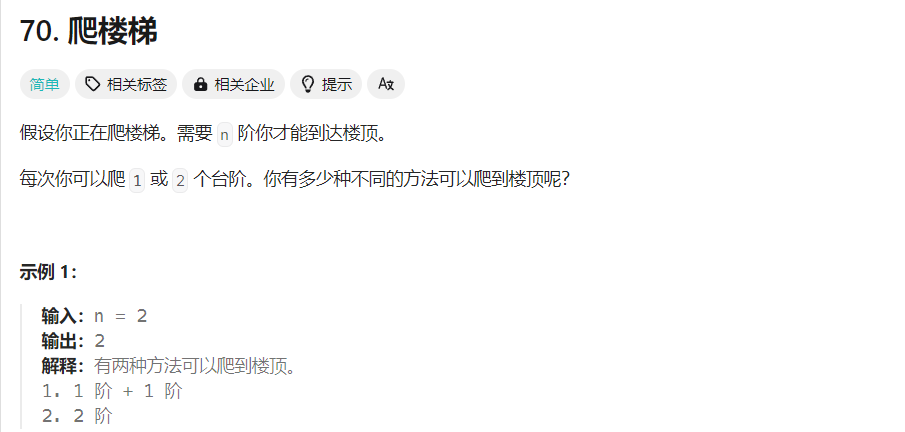
class Solution {
public:
    int climbStairs(int n) {
        vector<int>dp(n+1);
        if(n<=1)
            return 1;
        dp[1] = 1;
        dp[2] = 2;
        for(int i=3;i<=n;i++){
            dp[i] = dp[i-1] + dp[i-2];
        }
        return dp[n];
    }
};

三、746 使用最小花费爬楼梯

class Solution {
public:
    int minCostClimbingStairs(vector<int>& cost) {
        vector<int>dp(cost.size()+1);
        dp[0] = 0;
        dp[1] = 0;//因为可以选择从下标0或1开始爬，不需要花费
        for(int i=2;i<dp.size();i++){
            dp[i] = min(dp[i-1]+cost[i-1],dp[i-2]+cost[i-2]);
        }
        return dp[cost.size()];
    }
};