【DFS】I Like Matrix Forever!

Description

对一个 n ∗ m 的零矩阵 A 进行 q 次操作：
• 1 i j：将 A i,j 取反；
• 2 i：将矩阵 A 第 i 行的所有元素全部取反；
• 3 j：将矩阵 A 第 j 列的所有元素全部取反；
• 4 k：将矩阵 A 还原为第 k 次操作之后的状态。
进行每一次操作之后，询问当前矩阵所有元素的和。

Input

第一行包含三个整数 n，m 和 q。
之后 q 行每行包含两个或三个整数，表示一次操作的所有参数。

Output

共 q 行每行包含一个整数 ans，表示当前矩阵所有元素的和。

Sample Input

2 2 4
2 1
1 1 2
4 1
3 2

Sample Output

2
1
2
2

Hint

对于 30% 的数据：n,m ≤ 300，q ≤ 1000
对于 60% 的数据：n,m ≤ 1000，q ≤ 5000
对于 100% 的数据：n,m ≤ 1000，q ≤ 100000

思路

树形DFS
把他记作一棵树
如果操作不是4
就连接上一个操作，也就是节点
如果操作时4
就连接到他还原到哪一步的节点
样例数据的树为

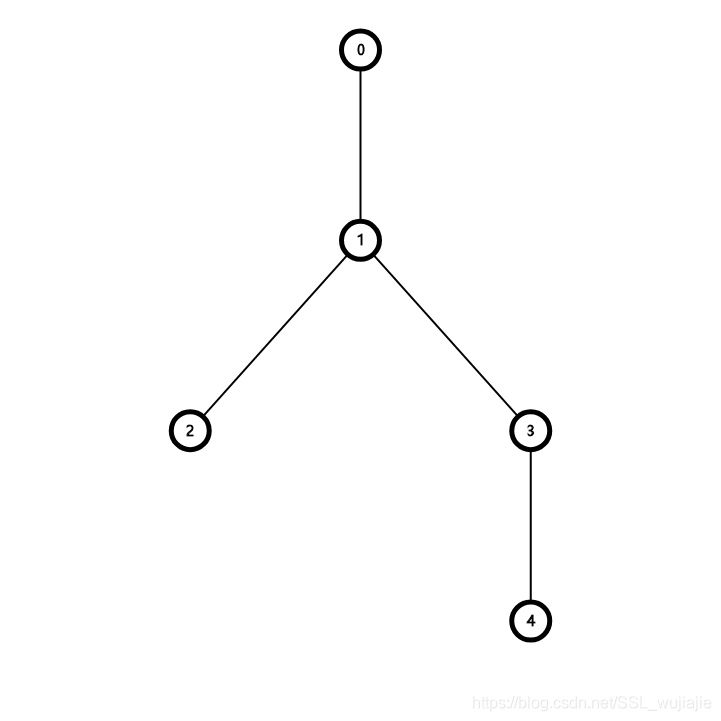
然后进行DFS
注意
要从0开始搜
因为有些可能会从头开始
其他详细见代码

//#pragma GCC optimize("O2")
//#pragma GCC optimize("O3")
#include<Algorithm>
#include<Iostream>
#include<Cstring>
#include<Cstdio>
#include<Cmath>
using namespace std;
int Ans[100250],k[100250],x[100250],y[100250];
int A[1025][1025],h[100250];
int Sum,n,m,tot,t;
struct whw
{
	int w,h;
}wh[100025];
void hw(int x,int y)
{wh[++t]=(whw){y,h[x]};h[x]=t;}//建边
int read() //快读
{
	int x=0,flag=1;char ch=getchar();
	while(ch<'0'||ch>'9'){if(ch=='-')flag=-1;ch=getchar();}
	while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
	return x*flag;
}
void write(int x)//快输
{
    if(x<0){x=-x;putchar('-');}
	if(x>9)write(x/10);
	putchar(x%10+48);
	return;
}
void Dfs(int dep)//树形DFS
{
	switch (k[dep])//进行操作
	{
		case 1:
		{
			Sum+=1-(A[x[dep]][y[dep]]<<1);
			A[x[dep]][y[dep]]^=1;
			break;
		}
		case 2:
		{
			for(int i=1;i<=m;++i)
			{
				Sum+=1-(A[x[dep]][i]<<1);
				A[x[dep]][i]^=1;
			}
			break;
		}
		case 3:
		{
			for(int i=1;i<=n;++i)
			{
				Sum+=1-(A[i][x[dep]]<<1);
				A[i][x[dep]]^=1;
			}
			break;
		}
	}
	Ans[dep]=Sum;//记录答案
	for(int i=h[dep];i;i=wh[i].h)//往下搜
		Dfs(wh[i].w);
	switch (k[dep])//还原操作
	{
		case 1:
		{
			Sum+=1-(A[x[dep]][y[dep]]<<1);
			A[x[dep]][y[dep]]^=1;
			break;
		}
		case 2:
		{
			for(int i=1;i<=m;++i)
			{
				Sum+=1-(A[x[dep]][i]<<1);
				A[x[dep]][i]^=1;
			}
			break;
		}
		case 3:
		{
			for(int i=1;i<=n;++i)
			{
				Sum+=1-(A[i][x[dep]]<<1);
				A[i][x[dep]]^=1;
			}
			break;
		}
	}
	return;
}
int main()
{
	n=read();m=read();tot=read();
	for(int i=1;i<=tot;++i)
	{
		k[i]=read();x[i]=read();
		if(k[i]==1)y[i]=read();
		if(k[i]!=4)hw(i-1,i);//如果不是4，就往下接
		else hw(x[i],i);//如果是4，往还原的地方下面接
	}
	Dfs(0);//从0开始
	for(int i=1;i<=tot;++i)write(Ans[i]);
	return 0;
}