ST表简介——处理RMQ问题的利器
前言:什么是RMQ,就是在线性表内处理出一段区间的最大值和最小值问题。如果你利用普通的for查找的话,时间复杂度为O(l-r+1),但是如果你用ST表预处理一下,时间复杂度为O(nlogn)加上每次查询的复杂度为O(1)是不是快捷很多。
比如一个线性表长度为1e5,查询次数为1e6,那么毫无疑问,朴素算法直接爆炸,
但是ST表就不会,而且到了后面的查询会十分迅速。
开始介绍算法原理,如果我们要存一个长度为n的线性表,并构建ST表的的话,我们要建一个
st[n][
n
l
o
g
2
\ n{log2}
nlog2] 这样长度的二维表。
设st_min[n][ n l o g 2 \ n{log2} nlog2],则st_min[i][j]所表示的内容则为i~i+2^j-1范围内的min值。那么对于st[i][0]时,很显然就是原数组[i]本身。那么我们怎么向j>0的范围扩展呢。
先放代码:
int t=log(n)/log(2)+1;
for(int j=1;j<t;j++)
for(int i=1;i<=n-(1<<j)+1;i++)
num1[i][j]=max(num1[i][j-1],num1[i+(1<<(j-1))][j-1]);
我们来看一下,为了确定覆盖了整个原数组的范围,要加上个一。
假设初始数据为这样:
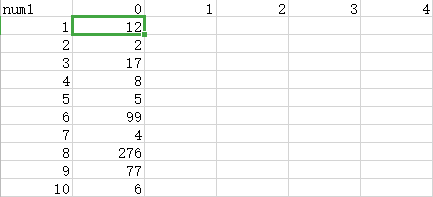
我们来走一下,第一步:i=j=1,num1[1][1]=min(num1[1][0],num[2][0]),是不是符合上面ST表的定义
那么就变成这样

第二步:i=2,j=1,num1[2][1]=min(num1[2][0],num1[3][0]);则第三步为:
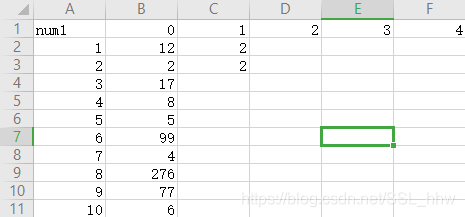
这个时候大家就知道for循环的大概一个趋势是一个下三角的趋势。(脑补一下)
那么预处理就完成了。接下来怎么查询的问题,已知查询区间,L和R,那么我们可以定义一个k,吧查询长度转换成上文的j,即:
k=log(r-l+1)/log(2);
那么我们怎么处理呢,我们知道,一个数它一般是不能一2^K表示出来的,所以单单只有num1[l][k]肯定是不够的,那么我们怎么样去“补全"这个区间呢?我们可以从r- 2^k 出发查找到r,那么这样就可保证覆盖了整个查找区间,如图所示。
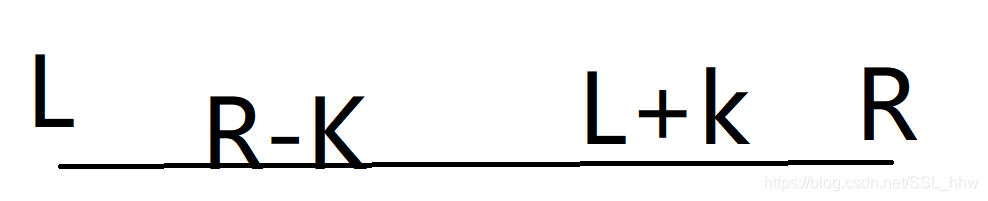
就是这个样子,推荐大家一个例题。
#CODE
#include<iostream>
#include<cstdio>
#include<cmath>
#include<cstring>
#include<algorithm>
using namespace std;
int n,m;
int a[50001];
int l,r;
int num1[50001][51],num2[50001][51];
int main()
{
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)
scanf("%d",&a[i]);
for(int i=1;i<=n;i++)
num1[i][0]=a[i],num2[i][0]=a[i];
int t=log(n)/log(2)+1;
for(int j=1;j<t;j++)
for(int i=1;i<=n-(1<<j)+1;i++)
num1[i][j]=max(num1[i][j-1],num1[i+(1<<(j-1))][j-1]),num2[i][j]=min(num2[i][j-1],num2[i+(1<<(j-1))][j-1]);
for(int i=1,k;i<=m;i++)
{
scanf("%d%d",&l,&r);
k=log(r-l+1)/log(2);
printf("%d\n",max(num1[l][k],num1[r-(1<<k)+1][k])-min(num2[l][k],num2[r-(1<<k)+1][k]));
}
return 0;
}





 本文介绍了如何使用ST表(Segment Tree)解决在线性表中查找区间最大值和最小值(RMQ)问题,通过预处理将查询时间复杂度降至O(nlogn) + O(1),在大规模数据和频繁查询场景中表现出色。
本文介绍了如何使用ST表(Segment Tree)解决在线性表中查找区间最大值和最小值(RMQ)问题,通过预处理将查询时间复杂度降至O(nlogn) + O(1),在大规模数据和频繁查询场景中表现出色。
















 1541
1541

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








