[DFS][类哈希][DP]坑带的树

最新推荐文章于 2025-02-16 23:03:20 发布

Vagari_

最新推荐文章于 2025-02-16 23:03:20 发布

阅读量345

点赞数

CC 4.0 BY-SA版权

本文链接：https://blog.youkuaiyun.com/SSL_QYH0Ice/article/details/81089060

本文讨论了一种特殊的无向图——仙人掌树，并提出了一个问题：如何通过节点重新编号，使得变换后的图与原图相同。文章通过DFS和动态规划（DP）方法分析解决方案，并提到在处理环的定义时需要考虑对称性，可以通过类哈希方法判断结构的对称或相等。最后给出了数据约束和样例输入输出。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

题目描述

“我不适合你，你有更好的未来。”
当小A当上主持的那一天，他接受记者采访的时候，回忆起了10年前小N离开自己的那句话。
小A出家，其实是因为他已经勘探到了宇宙的奥秘，他希望遁入佛门，通过自己的可修，创造出超越宇宙的秘法，从而突破宇宙的束缚，达到大无畏之境界。
好吧，小A最近碰到了一个挺恶心的问题。
首先，先介绍仙人掌树。仙人掌树是一张无向图，但是每个节点最多只会在一个环里面，而且这张图的环全部都是简单环，即A->B->C->A这种。
比如下图就是一颗仙人掌树。
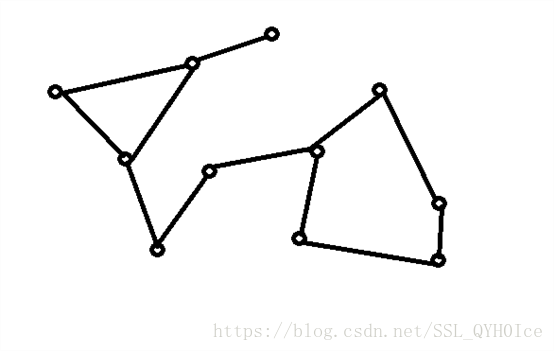
这里写图片描述
好的，知道了仙人掌树之后，我们现在要计算一个东西。
我们现在已经知道了一个N个节点的仙人掌树，称作为原图。接下来，我们要用1-N的一个排列A[1]-A[N]去变换这棵树，具体的，如果原图中有一条边i-j，那么变换出来的图中必须有一条A[i]-A[j]的边。同样的，如果变换出来的图中有一条A[i]-A[j]的边，那么原图中必有一条i-j的边。（简单而言就是点重新编号）
小A为了超脱宇宙的束缚，必须要知道，有多少种排列，可以使得变换出来的新图和原图是一模一样的，具体的，原图中如果存在一条i-j的边，新图也存在一条i-j的边，新图中存在一条i-j的边，原图中也存在i-j的边。
方案数目答案mod 1000000003。

Input
第一行有两个正整数，N和M，节点个数和边的个数。
接下来M行，每行有2个正整数S，T，表示一条原图的无向边。数据保证没有重边。

Output
一行一个正整数表示方案书目。

Sample Input
5 5
1 2
2 3
3 4
4 5
1 5

Sample Output
10
解释：
所有的答案包括(i,(i+1) % 5 + 1,(i+2) % 5 + 1,(i+3) % 5 + 1,(i+4) % 5 + 1)和(i,(i+4) % 5 + 1,(i+3) % 5 + 1,(i+2) % 5 + 1,(i+1) % 5 + 1)这两种类型。每种类型的i可以是12345，所以答案是2*5=10。

Data Constraint
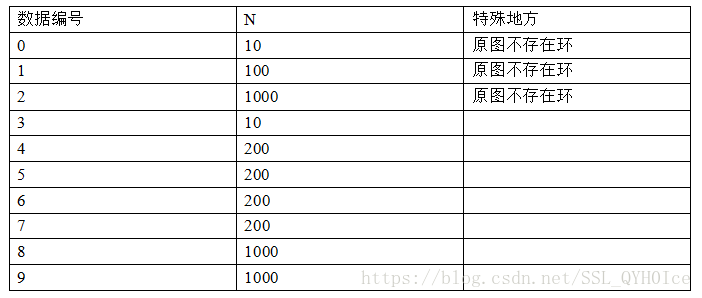
这里写图片描述

分析

我们把一棵以i为根的子树的同构方案总数即fi
那么我们有两种情况：
1、接下来走的点是该点的儿子（树的定义）
2、接下来走的点是该点的兄弟（环的定义）
儿子兄弟容易判断，跑个DFS就行
然后显然初始值为1，用乘积转移上来
然后对于环兄弟，值也差不多，但是注意：对于对称的环，我们要给方案数×2
那么问题上来了：怎么求几个点在结构上对称或相等呢？
我们想到了哈希（虽然我没有打，不过类似了）
可以给该点一个特征值，这个特征值由多重因素影响如：
1、所处深度
2、子树大小
3、环兄弟大小
还有一些可以自己加入，也可不加
但是我们考虑到，这样一棵树，以不同的点作为根可能会有结构完全相同的情况，那么我们需要判断根节点的特征值是否一样，一样就说明根节点也可以变换

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <memory.h>
#define rep(i,a,b) for (i=a;i<=b;i++)
typedef long long ll;
const int N=1001;
const int MOD=1e9+3;
using namespace std;
int n,m;
int to[N*(N-1)],nx[N*(N-1)],lt[2*N],fa[N],bel[2*N],sz[2*N],cnt=1,Cnt;
ll f[N],ty[N],fact[N];
bool b[N],bm[N*(N-1)];

void Add(int u,int v) {to[++cnt]=v;nx[cnt]=lt[u];lt[u]=cnt;}

void Init() {
    int i;
    scanf("%d%d",&n,&m);
    cnt=1;
    fact[0]=1;
    rep(i,1,n) fact[i]=fact[i-1]*i%MOD;
    rep(i,1,m) {
        int u,v;
        scanf("%d%d",&u,&v);
        Add(u,v);Add(v,u);
    }
    Cnt=n;
}

void Circle_to_point(int u,int f) {
    b[u]=1;fa[u]=f;
    for (int i=lt[u];i;i=nx[i])
    if (to[i]!=f)
    {
        if (b[to[i]]) {
            if (bel[to[i]]) continue;
            Cnt++;
            sz[Cnt]=1;bel[to[i]]=Cnt;fa[to[i]]=u;
            for (int j=u;j!=to[i];j=fa[j])
            sz[Cnt]++,bel[j]=Cnt;
        }
        else Circle_to_point(to[i],u);
    }
}

void Get_all_together() {
    int i;
    rep(i,1,n)
    if (!bel[i]) {
        bel[i]=++Cnt;
        sz[Cnt]++;
    }
}

void Solve(int root,int dep) {
    int i,j=1;
    f[root]=ty[root]=1;
    for (i=lt[root];i;i=nx[i])
    if (bel[root]!=bel[to[i]]&&!bm[i]) {
        bm[i]=bm[i^1]=1;
        Solve(to[i],dep+1);
        f[root]=f[root]*f[to[i]]%MOD;
        bm[i]=bm[i^1]=0;
    }
    int circle[N],crt=0,sot=0;
    ll sty[N];
    bool sym=1;
    if (!b[bel[root]]&&sz[bel[root]]>1) {
        b[bel[root]]=1;
        for (i=fa[root];i!=root;i=fa[i])
        Solve(i,dep+1),f[root]=f[root]*f[i]%MOD,circle[++crt]=i;
        rep(i,1,crt/2) if (ty[circle[i]]!=ty[circle[crt-i+1]]) {sym=0;break;}
        if (sym) f[root]=f[root]*2%MOD;
        b[bel[root]]=0;
    }
    for (i=lt[root];i;i=nx[i])
    if (bel[root]!=bel[to[i]]) sty[++sot]=ty[to[i]];
    sort(sty+1,sty+sot+1);
    rep(i,2,sot)
    if (sty[i]==sty[i-1]) j++;
    else f[root]=f[root]*fact[j]%MOD,j=1;
    f[root]=f[root]*fact[j]%MOD;
    rep(i,1,crt) sty[++sot]=ty[circle[i]]*sz[bel[root]]+min(i,crt-i+1);
    sort(sty+1,sty+sot+1);
    rep(i,1,sot) ty[root]=ty[root]*10+sty[i];
    ty[root]=ty[root]*dep;
}

int main() {
    Init();
    Circle_to_point(1,0);
    Get_all_together();
    memset(b,0,sizeof b);
    Solve(1,1);
    int i,j=1;
    ll ty1=ty[1],ans=f[1];
    rep(i,2,n) {
        memset(ty,0,sizeof ty);
        Solve(i,1);
        if (ty[i]==ty1) j++;
    }
    printf("%lld",ans*j%MOD);
}