如何判断模型中是否存在自相关？

在做回归分析，尤其是 时间序列回归、面板数据回归以及一些具有“顺序结构”的数据分析时，研究者最常担心的几个问题包括：多重共线性、异方差、自相关。其中，自相关（Autocorrelation）往往是最容易被忽视、但对模型破坏力极强的一个。

很多同学做完 OLS 回归后，以为只要显著性 OK、R² 好看，就可以放心写论文。但如果你的误差项存在自相关，那么 t 检验、F 检验、标准误差、显著性判断几乎都会 “统统失效”——模型可能在“骗你”。

为了避免在论文盲审、答辩或者科研中出错，我们必须学会：如何识别模型中是否存在自相关？

本文将系统讲解判断自相关的主要方式，并配套流程图、操作思路、判定标准，以及如何在 SPSSAU 中快速检测并自动输出诊断结果。

一、什么是自相关？

自相关（Autocorrelation）是指：回归模型中的残差项之间并非独立，而是彼此相关，尤其是随时间或序列位置变化出现规律性。最典型的情况是时间序列。例如：今年的误差项可能与去年的误差项相关；某一时段的预测不足或过度，会延续到之后。

直觉理解：就像气温变化具有连续性，误差如果也存在“惯性”，那就会呈现系统模式，而不是“完全随机”的白噪声。如果误差项相关，那么 OLS 的一个核心假设“独立性”就被破坏 → 标准误偏差 → 显著性判断失效。

二、我们为什么必须判断自相关？

自相关会导致：

• OLS 不再是有效（efficient）的，估计量方差偏大/偏小；
• t 值、F 值可能不可靠；
• 显著性检验失真；
• 预测不准确；
• 模型稳定性受损，容易产生伪回归假象。

在论文、项目报告、学术发表中，自相关是被严格审查的部分，尤其是在：

• 经济数据（GDP、CPI、汇率…）
• 金融数据（股价、收益率…）
• 教育连续数据（年度投入、产出…）
• 医疗连续观测数据
• 各类“时间序列结构”的研究中

几乎都不可避免。因此：“判断是否存在自相关”是一个高频且必不可少的步骤。

三、判断是否存在自相关的常见方法总览

下面列出学界与实务中最常见的判断标准：

1. DW（Durbin–Watson）检验 → 检查一阶自相关
2. LM 检验（Breusch–Godfrey Test） → 检查高阶自相关，应用更广
3. 残差图（ACF、PACF）观察法 → 直观判断
4. 滞后残差散点图 → 看是否存在趋势性
5. Run Test（游程检验） → 判断残差随机性
6. Ljung–Box Q 检验 → 时序模型常用
7. 对比模型调整前后 AIC/BIC
8. 在软件中使用自动诊断（如 SPSSAU）

为了更高效掌握，下文将所有方法做系统梳理，并配合操作逻辑与判断标准。

四、判断自相关的整体流程（Mermaid 流程图）

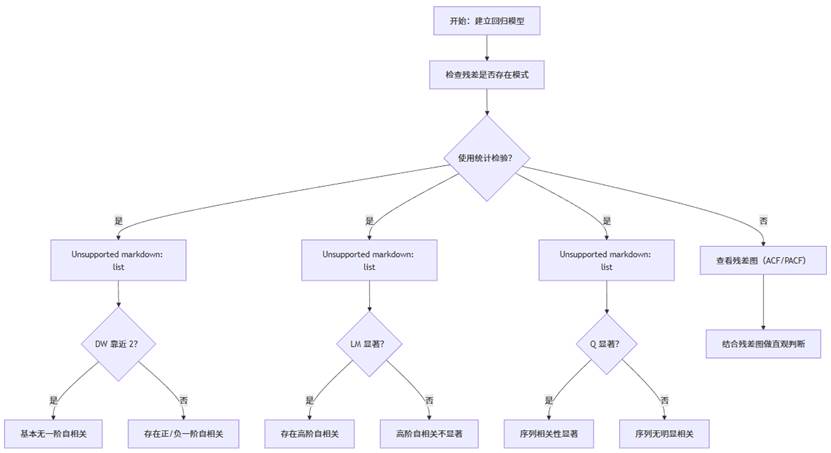
流程图说明：该图展示了判断残差自相关的完整路径，既可以通过统计量（DW、BG、LBQ），也可以通过图形（ACF/PACF、残差序列图）来辅助判断。
在实际科研中，建议使用：DW + BG + 图形法 作为常规组合。

方法 1：Durbin–Watson（DW）检验 —— 判断一阶自相关

DW 是最经典、最常用的自相关检验方法，对“一阶自相关”极其敏感。DW 越接近 2，说明越没有自相关。判断标准如下：

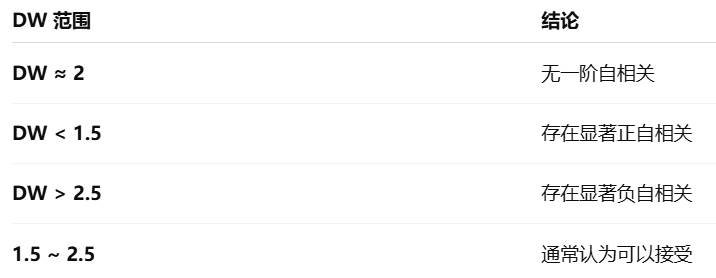
DW 的优点：简单易懂、输出自动化、大部分软件默认提供；

缺点：只能检验 一阶 自相关、部分模型结构下不适用（如带滞后变量）。

例如SPSSAU线性回归会直接输出D-W值：

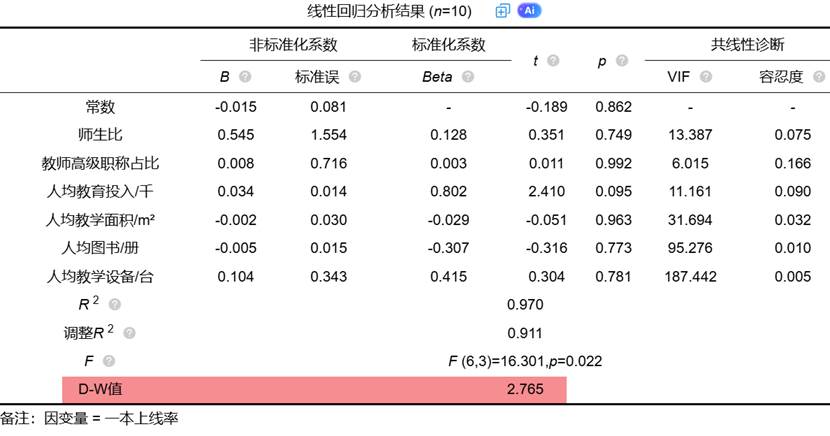
方法 2：Breusch–Godfrey LM 检验（BG 检验）——判断高阶自相关的首选

相比 DW 的局限，LM 检验（BG 检验）几乎适用于所有场景，是更强大、也更专业的自相关检验方法。LM 检验的逻辑——检查残差是否与其多个滞后项相关。

优点：可以检验 任意阶数的自相关；可以应用于含滞后因变量的模型；统计界普遍推荐。

判断标准：

• p < 0.05 → 存在自相关
• p ≥ 0.05 → 不存在自相关

方法 3：残差图（ACF/PACF 图）观察法

除了统计检验，图形是十分直观的辅助方式。

① ACF（自相关函数图）

若残差的 ACF 图中：多个滞后项显著超出置信区间 → 存在自相关；大部分在置信区间内 → 无明显自相关。

② PACF（偏自相关图）

PACF 进一步判断“控制前序滞后后”的相关性。常见特征：

• ACF 拖尾、PACF 截尾 → AR 型特征
• PACF 拖尾、ACF 截尾 → MA 型特征

虽然这是时间序列理论，但在判断残差结构中非常有帮助。

在 SPSSAU【计量经济研究】模块可选择【偏(自)相关图】，会直接输出ACF图和PACF图。

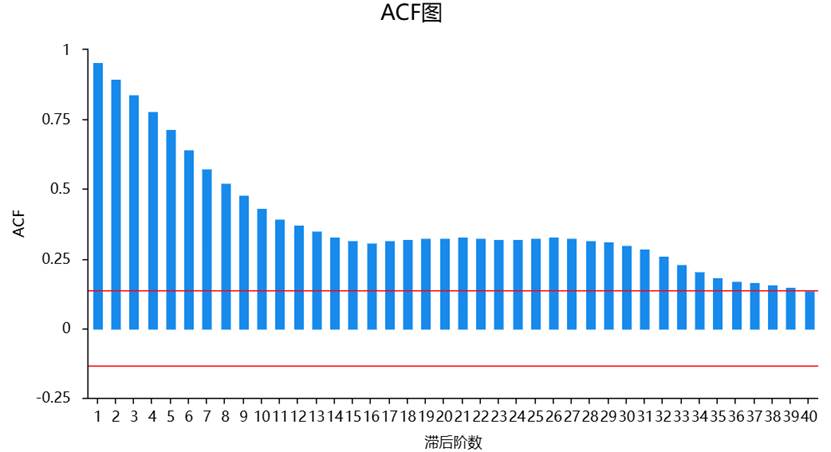
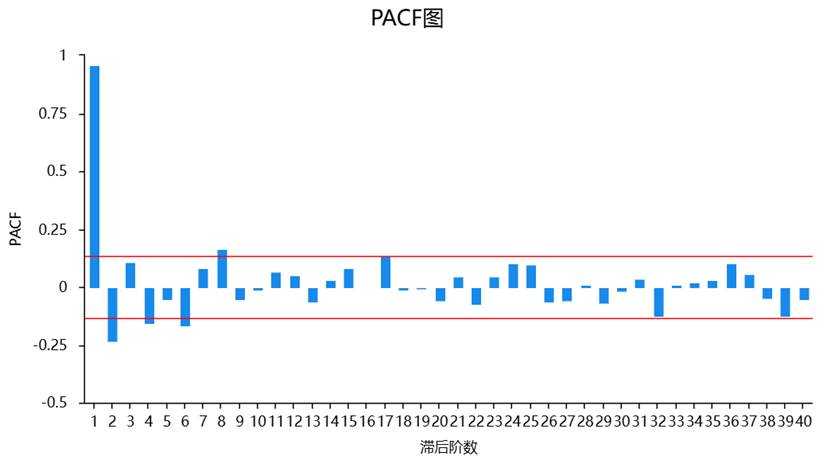
方法 4：残差序列图（滞后散点图）

这是一个非常简单但效果极高的方法。若残差散点图呈直线或曲线趋势 → 有自相关；若完全随机散布 → 无自相关。

方法 5：Ljung–Box Q 检验（时间序列模型必用）

在 ARIMA/时间序列分析中，Ljung–Box Q（LBQ）是判断残差是否为白噪声的重要方法。

判断标准：Q 检验的 p 值 < 0.05 → 残差非白噪声 → 存在自相关；p ≥ 0.05 → 可认为残差随机 → 无明显自相关。SPSSAU 的 ARIMA 模型模块也自动输出 LBQ 检验，非常适合写预测类论文。

结束语

自相关是回归分析中不可忽视的问题。如果不提前检查，很可能出现“模型显著但结论错误”的情况。
希望通过本文，你已经掌握了如何系统判断自相关，以及如何结合软件工具（如 SPSSAU）高效完成诊断。