主成分分析实例分析与软件操作

主成分分析(PCA)是一种常用的降维技术，通过线性变换将原始变量转换为一组线性不相关的变量(主成分)，广泛应用于综合评价、数据降维等领域。下面我将通过一个完整案例，详细介绍如何在SPSSAU(在线SPSS)中进行主成分分析。

一、案例背景

假设我们研究我国不同省份铁路运输能力情况，收集到以下指标数据：铁路客运量、铁路旅客周转量、铁路货运总量、铁路营业里程、铁路货物总周转量、铁路运输职工人数。

二、SPSSAU操作步骤

1.数据准备

• • 登录SPSSAU(网页SPSS)平台
  • 上传整理好的Excel数据文件

2.分析操作

• • 在【进阶方法】模块选择【主成分分析】
  • 将所有5个变量拖拽到右侧分析框
  • 勾选"成分得分"与"综合得分"选项
  • 点击"开始分析"按钮

3.关键设置说明

• • 标准化处理：由于指标量纲不同，SPSSAU会自动进行标准化
  • 主成分数量：可手动指定或由系统自动确定

三、结果解读

1. KMO和Bartlett检验

KMO值>0.7，说明数据适合做主成分分析

• Bartlett检验显著，拒绝变量独立的原假设

2.方差解释率表

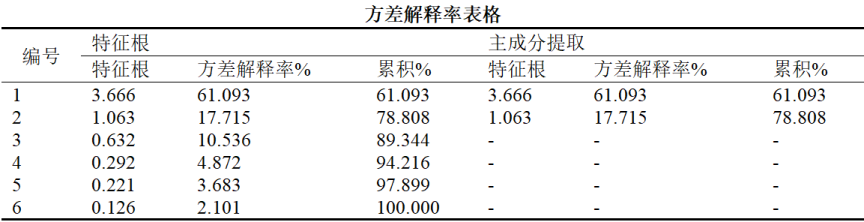
• 前两个主成分累计解释78.808%的方差，可保留这两个主成分

3. 载荷系数表格

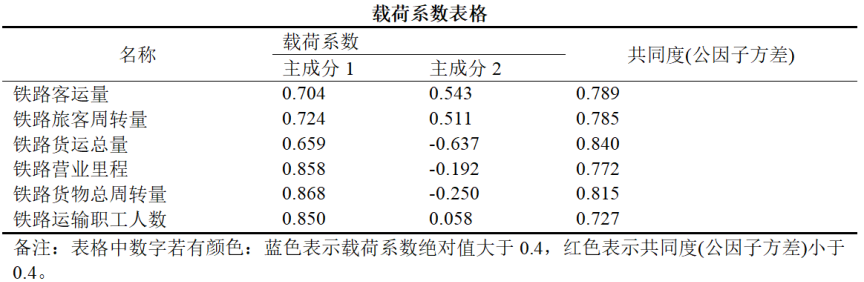
• 主成分1主要反映铁路营业里程、铁路货物总周转量、铁路运输职工人数
• 主成分2主要反映铁路客运量、铁路旅客周转量、铁路货运总量

4.线性组合系数矩阵

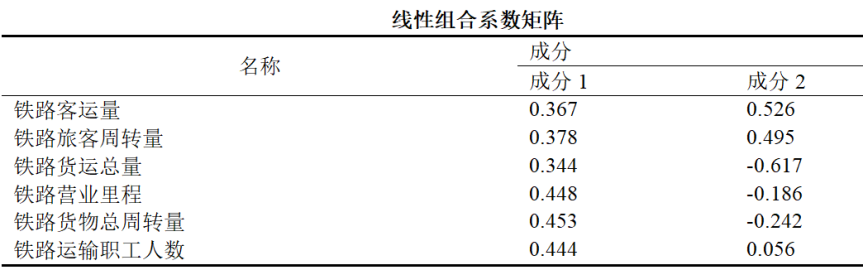
用于计算各样本在主成分上的得分：

• 成分得分F1=0.367*铁路客运量+0.378*铁路旅客周转量+0.344*铁路货运总量+0.448*铁路营业里程+0.453*铁路货物总周转量+0.444*铁路运输职工人数
• 成分得分F2=0.526*铁路客运量+0.495*铁路旅客周转量-0.617*铁路货运总量-0.186*铁路营业里程-0.242*铁路货物总周转量+0.056*铁路运输职工人数5. 综合得分计算

综合得分 = (61.093%*F1 + 17.715%*F2)/78.808%

SPSSAU(在线SPSS)会自动计算并保存成分得分与综合得分，可用于省份排名。

四、结果应用建议

1.综合评价：利用综合得分对各省铁路运输能力进行排名

2.降维处理：用两个主成分代替原始五个变量进行后续分析

3.指标权重：根据成分矩阵计算各指标的贡献权重

五、注意事项

1.主成分分析前建议进行标准化处理

2.主成分数量的选择需结合方差解释率和实际意义

3.主成分命名应基于载荷较高的原始变量

4.综合得分的计算方式可根据研究目的调整

通过SPSSAU(网页SPSS)平台，主成分分析变得简单高效，研究者可以快速完成从数据准备到结果解读的全流程分析。如需更详细的操作演示，可参考SPSSAU官方教程或帮助文档。