技术分享︱大型稀疏线性方程组求解技术——工业仿真的底层核心

最新推荐文章于 2025-11-25 00:06:26 发布

原创

最新推荐文章于 2025-11-25 00:06:26 发布 · 917 阅读

8 ·

CC 4.0 BY-SA版权

文章标签：

#算法 #稀疏线性方程组 #UNAP #流体力学 #结构力学 #高性能计算 #性能优化

技术分享︱大型稀疏线性方程组求解技术——工业仿真的底层核心的图1

一、背景

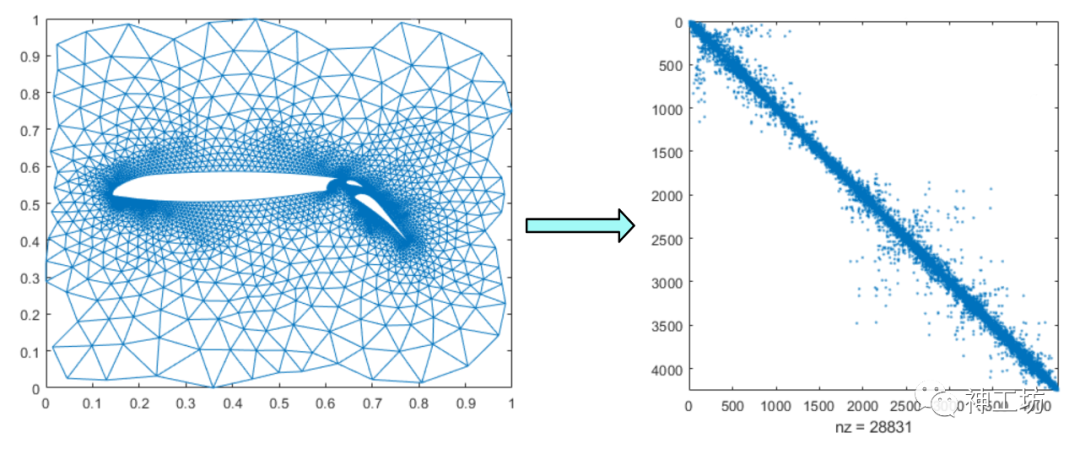
在工业仿真领域，对各种现实世界的问题进行数值模拟时，如流体动力学分析、电磁场仿真、结构力学应力应变分析等，其控制方程通常是偏微分方程组，在经过不同方法的隐式离散之后最终都可转化为大型稀疏线性方程组。随着人们对计算精度要求的不断提高，方程组的阶数也从上千阶、几十万阶提高到百万、千万阶甚至更高，所需的计算量以及存储需求也随之迅速膨胀。根据一般经验，方程组求解时间会占总计算时间的70%以上，往往是整个计算过程中的性能瓶颈。如果说求解器是工业CAE软件的核心模块，那么大型稀疏线性方程组的求解技术将毫无疑问是底层求解器的核心。

大型稀疏线性方程组求解技术——工业仿真的底层核心的图1 — NASA翼型网格经过离散得到的稀疏矩阵（素材来源于网络）

二、方法

众所周知，稀疏线性方程组的求解方法可以分为直接法和迭代法，两类方法各有优劣，特点比较如下：

迭代法[1]：

对于不同类型稀疏矩阵表现差异较大，存在收敛性与收敛速度问题，催生了许多预处理技术（Preconditioners）；
对原矩阵的编辑很少，SpMV(Sparse matrix-vector multiplication)是其核心运算；
内存需求小，求解速度较快，算法复杂度低；
较易实现并行化。

直接法[2]：

通用、稳定；通过前后处理，能够保证计算的收敛性与精度；
对原矩阵的编辑多（分解、排序、缩放等）；
内存需求大，求解速度慢，算法复杂度更高；
并行度有限。

其中迭代法的种类很多，可以分为定常（Stationary）迭代法与非定常迭代法[3]。经典的定常迭代法有Jacobi迭代法、Gauss-Seidel迭代法、SOR迭代法等，这些方法均可基于矩阵分裂推导得到；而在数值模拟中，非定常迭代法则显得更加重要，常见的有共轭梯度法（Conjugate Gradient CG）、广义最小残量方法（Generalized Minimal Residual GMRES）、稳定双共轭梯度法（Biconjugate Gradient Stabilized Bi-CGSTAB）等，这些算法都属于Krylov子空间方法。如今高性能共轭梯度（HPCG）测试包已成为国际上评测超级计算机性能的主要工具[4]，Krylov子空间方法也被评为20世纪最伟大的十大算法之一[5]。还有一些迭代算法则比较特殊，它们基于特殊结构和性质，例如我们耳熟能详的多重网格（Multigrid MG）方法，它更多地被称为数值计算领域中一种加速迭代收敛的技术，而不仅仅是一种单纯的算法。