【算法竞赛学习笔记】Purfer序列

原创于 2022-05-09 22:16:04 发布 · 554 阅读

2 ·

CC 4.0 BY-SA版权

文章标签：

#算法 #c++ #动态规划 #图论 #数据结构

ACM 同时被 3 个专栏收录

117 篇文章

订阅专栏

图论

19 篇文章

订阅专栏

组合数学

1 篇文章

订阅专栏

本文详细介绍了Prufer序列的性质及其在树的构造与计数中的应用，包括从序列构建树和从树构建序列的方法。此外，还讨论了完全图的生成树计数、图的连通方案数以及相关算法实现，如快速幂和基尔霍夫矩阵。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

title : Prufer
date : 2022-5-9
tags : ACM,计数，图论
author : Linno

文章目录

Purfer序列

Purfer序列

Prufer是一种将带符号的树用一个唯一的整数序列表示的方法。可以用来证明凯莱定理（Cayley’s formula:一个含有n个节点的完全图的生成树个数为 $n^{n-2}$ ,即带有标号的n个结点的无根树的个数为 $n^{n-2}$ ），也可以计算一个图加边使得图连通的方案。

性质

在构造完Prufer序列后原树中会剩下两个结点，其中一个一定是编号最大的点n
每个结点在序列中出现的次数是其度数-1（没有出现的就是叶子结点）
purfer序列与带编号无根树形成双射。
对于给定度数d1~dn的一棵无根树，一共有 $\frac{(n-2)!}{\prod_{i-1}^n(d_i-1)!},其中sum=n-2-\sum_{j-1}^{i-1}(d_j-1)$

对树建立Prufer序列

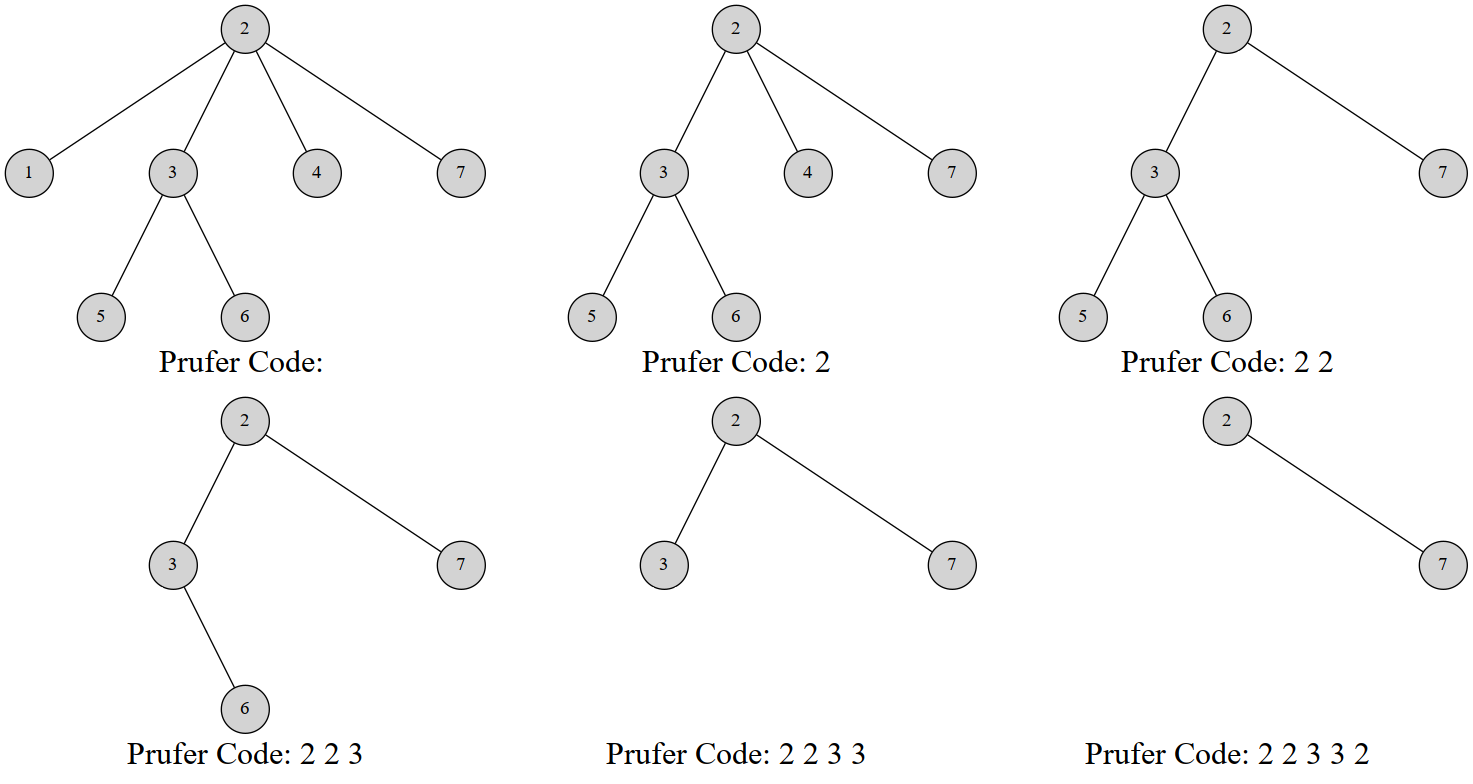
prufer

（图片转自OI-WIKI）

每次选择一个编号最小的叶子结点删除，如何在序列中记录下它连接到的那个结点，重复n-2次，就只剩下两个结点，算法结束。

堆O(nlogn)

vector<int>prufer(){
    set<int>leafs;
    for(int i=0;i<n;i++){
        deg[i]=adj[i].size();//adj为邻接矩阵
        if(deg[i]==1) leafs.insert(i);
    }
    vector<int>code(n-2);
    for(int i=0;i<n-2;i++){
        int leaf=*leafs.begin();
        leafs.erase(leafs.begin());
        kill[leaf]=1;
        int v;
        for(int u:adj[leaf]) if(!kill[u]) v=u;
        code[i]=v;
        if(--deg[v]==1) leafs.insert(v);
    }
    
}

线性构造

维护一个指针指向我们要删除的结点，一开始p指向编号最小的叶子节点。复杂度 $O (n)$ 操作过程如下：

删除p指向的结点，并检查是否产生新的叶子结点。
如果产生新的叶子结点x，我们比较p,x的大小关系。如果x>p，那么不做其他操作；否则立刻删除x，然后检查删除x后是否产生新的叶子结点，重复直到未产生新结点或者新结点的编号>p
让指针p指针直到遇到一个未被删除叶子结点为止。

vector<vector<int>>G;
vector<int>fa;
void dfs(int x){
    for(auto to:G[x]){
        if(to!=fa[x]) fa[to]=x,dfs(to);
    }
}

vector<int>prufer(){
    int n=G.size();
    fa.resize(n);
    fa[n-1]=-1;
    dfs(n-1);
    int ptr=-1;
    vector<int>deg(n);
    for(int i=0;i<n;i++){
        deg[i]=G[i].size();
        if(deg[i]==1&&ptr==-1) ptr=i;//找到编号最小的叶子结点
    }
    vector<int>code(n-2);
    int leaf=ptr;
    for(int i=0;i<n-2;i++){
        int nxt=fa[leaf];
        code[i]=nxt;
        if(--deg[nxt]==1&&nxt<prt) leaf=nxt; //如果父亲编号更小，就是下一个要删除的对象
        else{
            ptr++;
            while(deg[ptr]!=1) ptr++; //自增到最小的叶子节点
            leaf=ptr;
        }
    }
    return code;
}

对Prufer序列构造树

我们由上述性质可以求出树上每个点的度数，每次我们选择一个编号最小的叶子节点，与当前枚举到的Prufer序列进行连边，然后同时减掉两边的度数，重复n-2次就只剩下两个度数为1的结点了，其中一个为根节点，连接即可。

显然既可以用堆，也可以线性构造，就是上述过程的逆过程。

【模板】Prufer 序列

很简单的一道模板，但是自己写的比较繁琐就搬了洛谷的置顶题解。

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=5e6+7;
int n,o,f[N],p[N],d[N],ans;

inline void rd(int &data){	int x=0,f=1;char ch=getchar();while(ch<'0'||ch>'9'){if(ch=='-') f=f*-1;ch=getchar();}while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}data=f*x;}
inline void write(int x){if(x>9) write(x/10);putchar(x%10+'0');}

inline void TP(){
	for (int i = 1; i < n; i++) rd(f[i]), ++d[f[i]];
	for (int i = 1, j = 1; i <= n - 2; i++, j++) {
		while (d[j]) ++j; p[i] = f[j];
		while (i <= n - 2 && !--d[p[i]] && p[i] < j) p[i+1] = f[p[i]], ++i;
	}
	for (int i = 1; i <= n - 2; i++) ans ^= 1ll * i * p[i];
}

inline void PT() {
	for (int i = 1; i <= n - 2; i++) rd(p[i]), ++d[p[i]]; p[n-1] = n;
	for (int i = 1, j = 1; i < n; i++, j++) {
		while (d[j]) ++j; f[j] = p[i];
		while (i < n && !--d[p[i]] && p[i] < j) f[p[i]] = p[i+1], ++i;
	}
	for (int i = 1; i < n; i++) ans ^= 1ll * i * f[i];
}

signed main() {
	rd(n), rd(o), o == 1 ? TP() : PT(), write(ans);
	return 0;
}

UVA10843 Anne’s game

给定一个n个结点的完全图，求生成树的个数。

Purfer题解

题目满足Prufer序列的特性：

①prufer序列与无根树一一对应

②prufer序列中某个编号出现的次数就等于这个编号的结点在无根树中的度数-1

③n个点的完全图所构成的生成树计数就是 $n^{n-2}$

一个n个结点的树，它的prufer序列长度是n-2,每个位置都有n种选择，那么直接用快速幂就做完了。代码非常简短。

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int mod=2000000011ll;
 
int fpow(int a,int b){
	int res=1;
	while(b){
		if(b&1) res=res*a%mod;
		a=a*a%mod;
		b/=2;
	}
	return res;
}

int n,x;

signed main(){
	cin>>n;
	for(int i=1;i<=n;i++){
		cin>>x;
		cout<<"Case #"<<i<<": "<<fpow(x,x-2)<<"\n";
	}
	return 0;
}

基尔霍夫矩阵

这个矩阵基本可以解决生成树计数问题，复杂度 $O(n^3)$ （高斯消元）。原理在我MST的博客上有提到，构造方式很好记：K(基尔霍夫矩阵)=D(度数矩阵)-A(邻接表)

//#pragma GCC optimize("Ofast", "inline", "-ffast-math")
//#pragma GCC target("avx,sse2,sse3,sse4,mmx")
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int mod=2000000011ll;

//int read(){	int x=0,f=1;char ch=getchar();while(ch<'0'||ch>'9'){if(ch=='-') f=f*-1;ch=getchar();}while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}return x*f;}
//void write(int x){if(x>9) write(x/10);putchar(x%10+'0');}

int n,sq[105][105]; 

void Solve(int id){
	cin>>n;
	for(int i=1;i<=n;i++) for(int j=1;j<=n;j++){
		if(i==j) sq[i][j]=n-1;
		else sq[i][j]=-1;
	}
	int res=1;
	for(int i=2;i<=n;i++){
		for(int j=i+1;j<=n;j++){
			while(sq[j][i]){
				int t=sq[i][i]/sq[j][i];
				for(int k=i;k<=n;k++) sq[i][k]=(sq[i][k]-sq[j][k]*t);
				for(int k=i;k<=n;k++) swap(sq[i][k],sq[j][k]);
				res=-res;
			}
		}
		res*=sq[i][i];
		res%=mod;
	}
	if(res<0) res=-res;
	cout<<"Case #"<<id<<": "<<res<<"\n";
}

signed main(){
	ios::sync_with_stdio(0);
	cin.tie(0);cout.tie(0);
	int T;
	cin>>T;
	for(int t=1;t<=T;t++){
		Solve(t);
	}
	return 0;
}

图连通方案数

给定一个n个点m条边的带标号无向图有k个连通块，求添加k-1条边使得整个图连通的方案数。

如果是对已经有部分连通的图进行计数，恐怕没有比purfer序列更好处理的方法了。我们假设 $s_i$ 为每个连通块的大小，尝试对 $k$ 个连通块构造Prufer后，最终答案可以由结论得出： $ans=n^{k-2}\prod_{i=1}^ks_i$ （证明略）

树的计数

给定n个结点的树以及每个结点的度数，求满足条件的树有多少棵。

这道题正可以用于对最后一条性质的解释，考虑一个组合数学问题，度数为 $d_i$ 的结点会在prufer序列中出现 $d_i-1$ 次，那么题目就转化为了求 $d_i-1个i$ 的全排列个数。

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=200;

int n,C[N][N],deg[N];

void init(int m){
	for(int i=0;i<=m;i++){
		C[i][0]=C[i][i]=1;
		for(int j=1;j<=i;j++) C[i][j]=C[i-1][j]+C[i-1][j-1];
	}
}

signed main(){
	cin>>n;
	init(n);
	int sum=0,ans=1;
	for(int i=1;i<=n;i++) cin>>deg[i],sum+=deg[i]-1;
	if(n==1) cout<<(deg[1]^1ll)<<"\n";
	else if(sum!=n-2) cout<<"0\n";
	else{
		for(int i=1;i<=n;i++){
			if(!deg[i]){
				cout<<"0\n";
				return 0;
			}
			ans=ans*C[sum][deg[i]-1];
			sum-=deg[i]-1;
		}
		cout<<ans<<"\n";
	}
	return 0;
}