参考博客:https://blog.youkuaiyun.com/jiabiao1602/article/details/39177125
1.导入数据,R自带研究共线性的数据集
该数据集有7个变量,其中GNP.deflator可以作为yyy
rm(list=ls())
data=longley
print(data)

2.对全变量建立回归模型
model=lm(GNP.deflator~.,data=data)
summary(model)

结论:\color{red}{结论:}结论:从上面的结果可以看出,6个自变量中,只有两个变量的ppp值是显著的,此处看结果,要知道,多元线性回归的检验两种:一种是对回归方程的检验(F检验),另一种是对各个回归系数的检验,因为在回归方程中,即使回归方程显著,也不能说明每个自变量对y的影响都是显著的,因此我们总想从回归方程中剔除哪些次要的,可有可无的变量,重新建立更简单的方程。所以需要我们对每个自变量进行显著性检验。其中对自变量进行检验使用的t检验,从上面的summary()可以看出,Residual standard error是sigma_hat的估计
3.t检验计算,以GNP为例
# 显然此处p=6,此处的model$fitted_value与predict(model)是相同的值
# 这个和glm模型的值是不一样的
#
sig_2=sum((data$GNP.deflator-predict(model))*(data$GNP.deflator-predict(model)))
sig_hat=sqrt(sig_2/9)
#我一直不知道R里面把拟合的sigma_hat怎么取出来,可以以下面的方式
#不要以为summary(model)只是返回结果,如果输入a=summary(model)
#那么a是一个对象,那么就可以以a$sigma来获得sigma的估计值了
# 其余的属性也是类似的,其中拟合优度为a$r.squared
y=data[,1];
design_matrix=data[,c(-1)];
design_matrix=cbind(interc=rep(1,16),design_matrix)#直接Ctrl+enter就可以运行
design_matrix=as.matrix(design_matrix)
y=as.matrix(y)
beta=solve(t(design_matrix)%*%design_matrix)%*%t(design_matrix)%*%y
t_test=beta/(sqrt(diag(solve(t(design_matrix)%*%design_matrix)))*sig_hat)
print(t_test)

此处可以看到,对于截距项的检验也是t检验算出来的(虽然一般不看这个),
检验的公式为t=β^j(cjj)σ^t=\frac{\hat\beta_{j}}{\sqrt(c_{jj})\hat\sigma}t=(cjj)σ^β^j
4.计算方差扩大因子VIFVIFVIF,通常用来检验是否存在多重共线性
该包中的VIF不能对一元线性回归进行计算,会报错
library(car)
print(vif(model))#如果不用print,会有警告
#计算GNP的方差膨胀因子
data1=data[,c(-1)]
model_GNP=lm(GNP~.,data=data1)
R_Square=summary(model_GNP)$r.squared
VIF_GNP=1/(1-R_Square)
print(VIF_GNP)
可以看到完全一致,但是书上说VIF有另一个定义:对自变量进行中心标准化后,自变量的相关阵的主对角线元素VIF=cjjVIF=c_{jj}VIF=cjj,也是xjx_{j}xj的方差扩大因子
5.验证VIF的另一个定义
#自变量的相关阵
scale_fun=function(dat)
{
return(apply(dat,2,function(x) (x-mean(x))/sqrt(sum((x-mean(x))^2))))
}#这个地方和之前的标准化不一样,这个是除以了残差平方和的开平方,而非标准差
#,所以是不能是使用scale函数
scale_data=scale_fun(data[,c(-1)])
scale_data=as.matrix(scale_data);
C=solve(t(scale_data)%*%scale_data)
print(C)
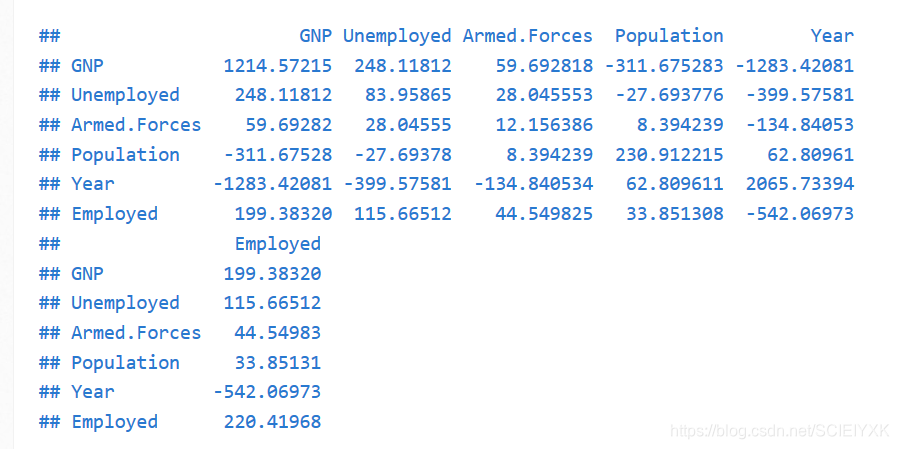
可以看到两者确实是相等的
6.画任意两个变量之间的相关关系图
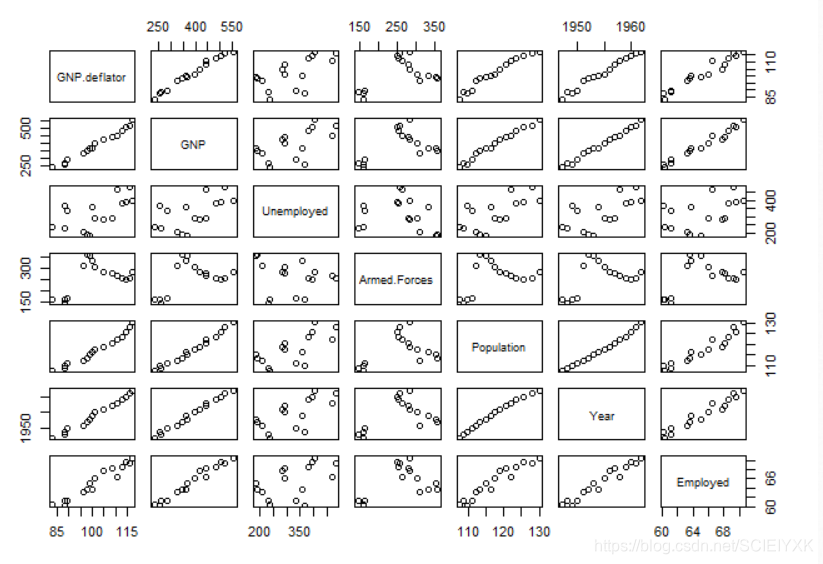
pairs(data)
cor(data[,2:7])
可以看到确实存在严重的多重共线性
7.利用step()函数来进行变量的筛选
model.step=step(model,direction = "backward")
summary(model.step)
8.验证一个东西,F−valueF-valueF−value 与R2R^2R2的关系
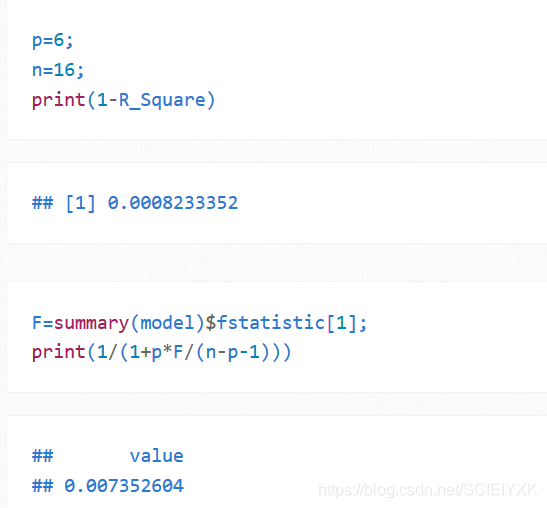
设自变量的个数为ppp,设计矩阵的维数为(n,p+1)(n,p+1)(n,p+1),那么1−R2=(1+Fpn−p−1)−11-R^{2}=(1+\frac{Fp}{n-p-1})^{-1}1−R2=(1+n−p−1Fp)−1
p=6;
n=16;
print(1-R_Square)
F=summary(model)$fstatistic[1];
print(1/(1+p*F/(n-p-1)))





 本文通过R语言介绍方差膨胀因子(VIF)的概念及其在检测多重共线性中的应用。首先导入研究共线性的数据集,建立回归模型,接着对自变量进行t检验,计算VIF值,并验证其另一种定义。通过相关关系图发现存在严重的多重共线性问题。最后,使用step()函数筛选变量,并探讨F-value与R2的关系。
本文通过R语言介绍方差膨胀因子(VIF)的概念及其在检测多重共线性中的应用。首先导入研究共线性的数据集,建立回归模型,接着对自变量进行t检验,计算VIF值,并验证其另一种定义。通过相关关系图发现存在严重的多重共线性问题。最后,使用step()函数筛选变量,并探讨F-value与R2的关系。

















 2466
2466

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








