Matlab在信号处理中的基本应用———学习笔记
第0个实例——matlab基本操作(FFT频谱分析)
设计要求
1.用MATLAB产生正弦波及白噪声信号,并显示各自时域波形图
2.进行FFT变换,显示各自频谱图。
3.做出两种种信号的均方根图谱,功率图谱,以及对数方均根图谱。
4.用IFFT傅里叶反变换恢复信号,并显示时域波形图。

%*********************正弦波*********************
clc;
fs=60; %抽样频率100Hz
N=128; %采样点数
t=0:1/fs:(N-1)/fs; %时域长度=点数 x 采样间隔=点数/采样频率
f0=10; %信号1的频率10HZ
x=sin(2*pi*f0*t);
figure(1);subplot(231);plot(t,x);grid;
xlabel("时间/s");ylabel("幅度");title("时域波形");
%*********************进行FFT变换******************
y=fftshift(fft(x,N));
mag=abs(y);
f=(floor(-(N-1)/2):floor((N-1)/2))/(N-1)*fs;%乘以信号长度分之一(频率分辨率)
subplot(232);plot(f,mag);grid;axis([-50, 50, 0, 100]);
xlabel("频率/Hz");ylabel("幅值");title("幅频图");

求三种谱,先忽略
ifft恢复出原信号
fftshift 将零频率移到中点。 用法y=fftshift(fft(x,N));
ifftshift 就是撤消 fftshift 的结果。 用法y=fftshift(fft(x2,N));
%*********************用ifft恢复原始信号******************
x2=ifft(ifftshift(y),N);
t2=(0:length(x2)-1)/fs;
subplot(233);plot(t2,x2);grid;
xlabel("时间/s");ylabel("幅度");title("恢复时域波形");
%*********************恢复信号进行FFT变换******************
y=fftshift(fft(x2,N));
mag=abs(y);
f=(floor(-(N-1)/2):floor((N-1)/2))/(N-1)*fs;
%f=(0:length(y)-1)*fs/length(y);
subplot(234);plot(f,mag);grid;axis([-50, 50, 0, 100]);
xlabel("频率/Hz");ylabel("幅值");title("恢复信号的幅频图");
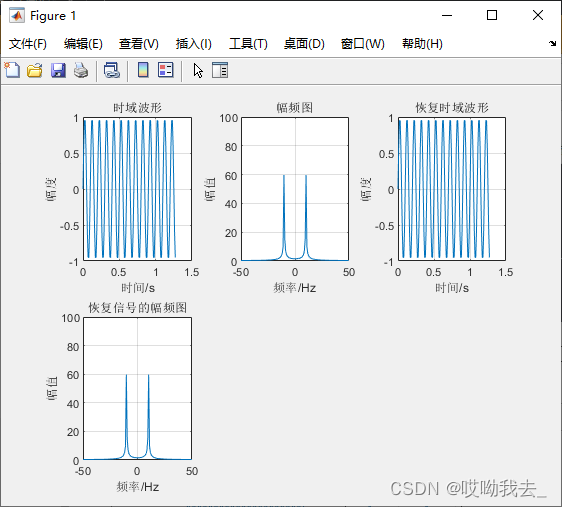





 该博客介绍了如何使用MATLAB进行信号处理,包括生成正弦波和白噪声信号的时域波形,进行FFT变换展示幅频图,以及利用IFFT恢复原始信号并重新进行FFT变换。此外,还涉及了信号的均方根、功率和对数方均根图谱的绘制。
该博客介绍了如何使用MATLAB进行信号处理,包括生成正弦波和白噪声信号的时域波形,进行FFT变换展示幅频图,以及利用IFFT恢复原始信号并重新进行FFT变换。此外,还涉及了信号的均方根、功率和对数方均根图谱的绘制。
















 1082
1082

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








