例子
接下来我们考虑一些随机问题,并展示如何使用RM算法来解决它们。
首先,考虑简单的均值估计问题:计算
w=E[X]w = \mathbb{E}[X]w=E[X]
基于X的一些独立同分布样本{x}。
- 通过写出g(w)=w−E[X]g(w) = w - \mathbb{E}[X]g(w)=w−E[X],我们可以将该问题重新表述为一个根查找问题
g(w)=0g(w) = 0g(w)=0
- 由于我们只能获得X的样本{x},带噪声的观测为
g~(w,η)=w−x=(w−E[X])+(E[X]−x)≐g(w)+η\tilde{g}(w,η) = w - x = (w - \mathbb{E}[X]) + (\mathbb{E}[X] - x) \doteq g(w) + ηg~(w,η)=w−x=(w−E[X])+(E[X]−x)≐g(w)+η
- 求解g(w)=0g(w) = 0g(w)=0的RM算法为
wk+1=wk−αkg~(wk,ηk)=wk−αk(wk−xk)w_{k+1} = w_k - α_k\tilde{g}(w_k,η_k) = w_k - α_k(w_k - x_k)wk+1=wk−αkg~(wk,ηk)=wk−αk(wk−xk)
其次,考虑一个稍微复杂一点的问题。即估计函数v(X)的均值,
w=E[v(X)]w = \mathbb{E}[v(X)]w=E[v(X)]
基于X的一些独立同分布随机样本{x}。
- 为了解决这个问题,我们定义
g(w)=w−E[v(X)]g~(w,η)=w−v(x)=(w−E[v(X)])+(E[v(X)]−v(x))≐g(w)+ηg(w) = w - \mathbb{E}[v(X)] \\ \tilde{g}(w,η) = w - v(x) = (w - \mathbb{E}[v(X)]) + (\mathbb{E}[v(X)] - v(x)) \doteq g(w) + ηg(w)=w−E[v(X)]g~(w,η)=w−v(x)=(w−E[v(X)])+(E[v(X)]−v(x))≐g(w)+η
- 然后,这个问题就变成一个根查找问题:g(w)=0g(w) = 0g(w)=0。相应的RM算法为
wk+1=wk−αkg~(wk,ηk)=wk−αk[wk−v(xk)]w_{k+1} = w_k - α_k\tilde{g}(w_k,η_k) = w_k - α_k[w_k - v(x_k)]wk+1=wk−αkg~(wk,ηk)=wk−αk[wk−v(xk)]
第三,考虑一个更复杂的问题:计算
w=E[R+γv(X)]w = \mathbb{E}[R + γv(X)]w=E[R+γv(X)]
其中R, X是随机变量,γ是一个常数,v(·)是一个函数。
- 假设我们可以获得X和R的样本{x}和{r}。我们定义
g(w)=w−E[R+γv(X)]g~(w,η)=w−[r+γv(x)]=(w−E[R+γv(X)])+(E[R+γv(X)]−[r+γv(x)])≐g(w)+ηg(w) = w - \mathbb{E}[R + γv(X)] \\ \tilde{g}(w,η) = w - [r + γv(x)]= (w - \mathbb{E}[R + γv(X)]) + (\mathbb{E}[R + γv(X)] - [r + γv(x)])\doteq g(w) + ηg(w)=w−E[R+γv(X)]g~(w,η)=w−[r+γv(x)]=(w−E[R+γv(X)])+(E[R+γv(X)]−[r+γv(x)])≐g(w)+η - 然后,这个问题就变成一个根查找问题:g(w)=0g(w) = 0g(w)=0。相应的RM算法为
wk+1=wk−αkg~(wk,ηk)=wk−αk[wk−(rk+γv(xk))]w_{k+1} = w_k - α_k\tilde{g}(w_k,η_k) = w_k - α_k[w_k - (r_k + γv(x_k))]wk+1=wk−αkg~(wk,ηk)=wk−αk[wk−(rk+γv(xk))]
state value的时间差分学习
算法描述
算法所需的数据/经验:
(s0,r1,s1,...,st,rt+1,st+1,...)(s_0, r_1, s_1,..., s_t, r_{t+1}, s_{t+1},...)(s0,r1,s1,...,st,rt+1,st+1,...) 或 {(st,rt+1,st+1)}t\{(s_t, r_{t+1}, s_{t+1})\}_t{(st,rt+1,st+1)}t 是按照给定策略π生成的。
这都是记录智能体在环境中按策略π交互的轨迹,每个元组(st,rt+1,st+1)(s_t, r_{t+1}, s_{t+1})(st,rt+1,st+1)表示在状态sts_tst执行动作后获得奖励rt+1r_{t+1}rt+1并转移到st+1s_{t+1}st+1。
核心目标:学习估计策略π下的状态值函数vπ(st)v_π(s_t)vπ(st),即从状态sts_tst出发的长期累积回报期望
TD学习算法为
vt+1(st)=vt(st)−αt(st)[vt(st)−[rt+1+γvt(st+1)]],(1)vt+1(s)=vt(s),∀s≠st,(2)v_{t+1}(s_t) = v_t(s_t) - α_t(s_t)[v_t(s_t) - [r_{t+1} + γv_t(s_{t+1})]], \quad (1) \\
v_{t+1}(s) = v_t(s), \quad \forall s \neq s_t, \quad (2)vt+1(st)=vt(st)−αt(st)[vt(st)−[rt+1+γvt(st+1)]],(1)vt+1(s)=vt(s),∀s=st,(2)
其中t=0,1,2,...t = 0,1,2,...t=0,1,2,...。
- vt(st)v_t(s_t)vt(st):当前对状态sts_tst的估值,即vπ(st)v_π(s_t)vπ(st)的估计状态值
- αt(st)α_t(s_t)αt(st):是sts_tst在时间t的学习率(0 < α < 1)
- rt+1r_{t+1}rt+1:从sts_tst到st+1s_{t+1}st+1获得的即时奖励reward
- γγγ:折扣因子(0 ≤ γ ≤ 1)
- vt(st+1)v_t(s_{t+1})vt(st+1):当前对下一个状态st+1s_{t+1}st+1的估值
公式(1)表示在时间t,只更新访问状态sts_tst的值,
公式(2)表示未访问状态s≠sts \neq s_ts=st的值保持不变。
公式变形: vt+1(st)=(1−α)vt(st)+α[rt+1+γvt(st+1)]v_{t+1}(s_t) = (1 - α)v_t(s_t) + α[r_{t+1} + γv_t(s_{t+1})]vt+1(st)=(1−α)vt(st)+α[rt+1+γvt(st+1)] (可看作当前估值与TD目标的加权平均)
算法属性
公式拆解
TD算法可以被注解为:
vt+1(st)⏟new estimate=vt(st)⏞current estimate−αt(st)[vt(st)−[rt+1+γvt(st+1)]⏟TD target vˉt⏞TD error δt],(3)
\underbrace{v_{t+1}(s_t)}_{\textcolor{red}{\text{new estimate}}} = \overbrace{v_t(s_t)}^{\textcolor{red}{\text{current estimate}}} - \alpha_t(s_t) \bigg[ \overbrace{v_t(s_t) - \underbrace{\left[ r_{t+1} + \gamma v_t(s_{t+1}) \right]}_{\textcolor{red}{\text{TD target } \bar{v}_t}}}^{\textcolor{red}{\text{TD error } \delta_t}} \bigg],\quad (3)
new estimatevt+1(st)=vt(st)current estimate−αt(st)[vt(st)−TD target vˉt[rt+1+γvt(st+1)]TD error δt],(3)
其中左边vt+1(st)v_{t+1}(s_t)vt+1(st)为新估计,vt(st)v_t(s_t)vt(st)为当前估计,[rt+1+γvt(st+1)][r_{t+1} + γv_t(s_{t+1})][rt+1+γvt(st+1)]为TD目标,
方括号内的整个表达式为TD误差δtδ_tδt。
这里,vˉt≐rt+1+γv(st+1)\bar{v}_t \doteq r_{t+1} + γv(s_{t+1})vˉt≐rt+1+γv(st+1)被称为TD目标,是当前状态sts_tst的即时奖励加上下一状态st+1s_{t+1}st+1估值的折扣值,作为当前状态估值的 “短期目标”。
δt≐v(st)−[rt+1+γv(st+1)]=v(st)−vˉtδ_t \doteq v(s_t) - [r_{t+1} + γv(s_{t+1})] = v(s_t) - \bar{v}_tδt≐v(st)−[rt+1+γv(st+1)]=v(st)−vˉt被称为TD误差,是当前估值与 TD 目标的差值。
显然,新估计vt+1(st)v_{t+1}(s_t)vt+1(st)是当前估计vt(st)v_t(s_t)vt(st)和TD误差的组合。
分析拆解项
首先,为什么vˉt\bar{v}_tvˉt被称为TD目标?
这是因为算法将v(st)v(s_t)v(st)驱动向vˉt\bar{v}_tvˉt。
为了看到这一点,
vt+1(st)=vt(st)−αt(st)[vt(st)−vˉt] ⟹ vt+1(st)−vˉt=vt(st)−vˉt−αt(st)[vt(st)−vˉt] ⟹ vt+1(st)−vˉt=[1−αt(st)][vt(st)−vˉt] ⟹ ∣vt+1(st)−vˉt∣=∣1−αt(st)∣∣vt(st)−vˉt∣v_{t+1}(s_t) = v_t(s_t) - α_t(s_t)[v_t(s_t) - \bar{v}_t] \\ \implies v_{t+1}(s_t) - \bar{v}_t = v_t(s_t) - \bar{v}_t - α_t(s_t)[v_t(s_t) - \bar{v}_t] \\ \implies v_{t+1}(s_t) - \bar{v}_t = [1 - α_t(s_t)][v_t(s_t) - \bar{v}_t] \\ \implies |v_{t+1}(s_t) - \bar{v}_t| = |1 - α_t(s_t)||v_t(s_t) - \bar{v}_t|vt+1(st)=vt(st)−αt(st)[vt(st)−vˉt]⟹vt+1(st)−vˉt=vt(st)−vˉt−αt(st)[vt(st)−vˉt]⟹vt+1(st)−vˉt=[1−αt(st)][vt(st)−vˉt]⟹∣vt+1(st)−vˉt∣=∣1−αt(st)∣∣vt(st)−vˉt∣
由于αt(st)α_t(s_t)αt(st)是一个小的正数,我们有0<1−αt(st)<10 < 1 - α_t(s_t) < 10<1−αt(st)<1因此,∣vt+1(st)−vˉt∣≤∣vt(st)−vˉt∣|v_{t+1}(s_t) - \bar{v}_t| \leq |v_t(s_t) - \bar{v}_t|∣vt+1(st)−vˉt∣≤∣vt(st)−vˉt∣这意味着v(st)v(s_t)v(st)被驱动向vˉt\bar{v}_tvˉt!
第二,TD error的解释是什么?
δt=v(st)−[rt+1+γv(st+1)]\delta_t = v(s_t) - [r_{t+1} + \gamma v(s_{t+1})]δt=v(st)−[rt+1+γv(st+1)]
- 它是两个连续时间步之间的差异。
- 它反映了vtv_tvt和vπv_\pivπ之间的不足。为了说明这一点,当使用真实值函数vπv_\pivπ时,误差为δπ,t\delta_{\pi,t}δπ,t,记为
δπ,t≐vπ(st)−[rt+1+γvπ(st+1)]\delta_{\pi,t} \doteq v_\pi(s_t) - [r_{t+1} + \gamma v_\pi(s_{t+1})]δπ,t≐vπ(st)−[rt+1+γvπ(st+1)]
注意,根据贝尔曼方程,真实值函数有vπ(st)=E[Rt+1+γvπ(St+1)∣St=st]v_\pi(s_t) = \mathbb{E}[R_{t+1} + \gamma v_\pi(S_{t+1}) | S_t = s_t]vπ(st)=E[Rt+1+γvπ(St+1)∣St=st],那么δπ,t\delta_{\pi,t}δπ,t期望必然为0,即
E[δπ,t∣St=st]=vπ(st)−E[Rt+1+γvπ(St+1)∣St=st]=0.\mathbb{E}[\delta_{\pi,t}|S_t = s_t] = v_\pi(s_t) - \mathbb{E}[R_{t+1} + \gamma v_\pi(S_{t+1})|S_t = s_t] = 0.E[δπ,t∣St=st]=vπ(st)−E[Rt+1+γvπ(St+1)∣St=st]=0. - 如果vt=vπv_t = v_\pivt=vπ,那么δt\delta_tδt应该为零(在期望意义上)。
- 因此,如果δt\delta_tδt不为零,则vtv_tvt不等于vπv_\pivπ。
- TD error可以被解释为innovation,这意味着从经验(st,rt+1,st+1)(s_t, r_{t+1}, s_{t+1})(st,rt+1,st+1)中获得的新信息。
其他特性:
vt+1(st)=vt(st)−αt(st)[vt(st)−[rt+1+γvt(st+1)]],v_{t+1}(s_t) = v_t(s_t) - α_t(s_t)[v_t(s_t) - [r_{t+1} + γv_t(s_{t+1})]],vt+1(st)=vt(st)−αt(st)[vt(st)−[rt+1+γvt(st+1)]],
- 上式中的TD算法仅估计给定策略的状态价值。
- 它不估计动作价值。
- 它不搜索最优策略。
稍后,我们将了解如何估计动作价值,然后搜索最优策略。
尽管如此,(3)中的TD算法对于理解核心思想是基础的。
算法思想
首先,贝尔曼方程的一个新表达式。
π的状态价值的定义是
vπ(s)=E[R+γG∣S=s],s∈S(4)v_\pi(s) = \mathbb{E}[R + \gamma G|S = s], \quad s \in \mathcal{S} \quad (4)vπ(s)=E[R+γG∣S=s],s∈S(4)
其中G是折扣回报。由于
E[G∣S=s]=∑aπ(a∣s)∑s′p(s′∣s,a)vπ(s′)=E[vπ(S′)∣S=s],\mathbb{E}[G|S = s] = \sum_a \pi(a|s)\sum_{s'} p(s'|s,a)v_\pi(s') = \mathbb{E}[v_\pi(S')|S = s],E[G∣S=s]=a∑π(a∣s)s′∑p(s′∣s,a)vπ(s′)=E[vπ(S′)∣S=s],
其中S’是下一个状态,我们可以将(4)重写为
vπ(s)=E[R+γvπ(S′)∣S=s],s∈S.(5)v_\pi(s) = \mathbb{E}[R + \gamma v_\pi(S')|S = s], \quad s \in \mathcal{S}. \quad (5)vπ(s)=E[R+γvπ(S′)∣S=s],s∈S.(5)
方程(5)是Bellman方程的另一种表达式。它有时被称为Bellman期望方程,是设计和分析TD算法的重要工具。
第二,使用RM算法求解(5)中的Bellman方程。
特别地,通过定义
g(v(s))=v(s)−E[R+γvπ(S′)∣s],g(v(s)) = v(s) - \mathbb{E}[R + \gamma v_\pi(S')|s],g(v(s))=v(s)−E[R+γvπ(S′)∣s],
我们可以将(5)重写为
g(v(s))=0g(v(s)) = 0g(v(s))=0
由于我们只能获得R和S’的样本r和s’,我们所拥有的噪声观测是
g~(v(s))=v(s)−[r+γvπ(s′)]=(v(s)−E[R+γvπ(S′)∣s])⏟g(v(s))+(E[R+γvπ(S′)∣s]−[r+γvπ(s′)])⏟η\tilde{g}(v(s)) = v(s) - [r + \gamma v_\pi(s')] \\ = \underbrace{(v(s) - \mathbb{E}[R + \gamma v_\pi(S')|s])}_{g(v(s))} + \underbrace{(\mathbb{E}[R + \gamma v_\pi(S')|s] - [r + \gamma v_\pi(s')])}_{\eta}g~(v(s))=v(s)−[r+γvπ(s′)]=g(v(s))(v(s)−E[R+γvπ(S′)∣s])+η(E[R+γvπ(S′)∣s]−[r+γvπ(s′)])
因此,用于解决g(v(s)) = 0的RM算法是
vk+1(s)=vk(s)−αkg~(vk(s))=vk(s)−αk(vk(s)−[rk+γvπ(sk′)]),k=1,2,3,…(6)v_{k+1}(s) = v_k(s) - \alpha_k\tilde{g}(v_k(s))\\ = v_k(s) - \alpha_k\left(v_k(s) - [r_k + \gamma v_\pi(s'_k)]\right), \quad k = 1, 2, 3, \ldots \quad (6)vk+1(s)=vk(s)−αkg~(vk(s))=vk(s)−αk(vk(s)−[rk+γvπ(sk′)]),k=1,2,3,…(6)
其中vk(s)v_k(s)vk(s)是第k步时vπ(s)v_π(s)vπ(s)的估计值;rkr_krk, v(sk′)v(s'_k)v(sk′)是第k步获得的reward, 和它到达的下一个状态S’的状态价值的样本。
RM算法(6)有两个值得特别注意的假设。
• 我们必须拥有经验集{(s,r,s′)(s, r, s')(s,r,s′)},对于k = 1, 2, 3, …
• 我们假设对于任何s′s's′,vπ(s′)v_π(s')vπ(s′)已经是已知的。
因此,用于解决g(v(s))=0g(v(s)) = 0g(v(s))=0的RM算法是
vk+1(s)=vk(s)−αkg~(vk(s))=vk(s)−αk(vk(s)−[rk+γvπ(sk′)]),k=1,2,3,…v_{k+1}(s) = v_k(s) - \alpha_k\tilde{g}(v_k(s)) \\ = v_k(s) - \alpha_k\left(v_k(s) - [r_k + \gamma v_\pi(s'_k)]\right), \quad k = 1,2,3,\ldotsvk+1(s)=vk(s)−αkg~(vk(s))=vk(s)−αk(vk(s)−[rk+γvπ(sk′)]),k=1,2,3,…
其中vk(s)v_k(s)vk(s)是第k步时vπ(s)v_\pi(s)vπ(s)的估计值;rk,sk′r_k, s'_krk,sk′是第k步获得的R,S′R, S'R,S′的样本。
为了消除RM算法中的两个假设,我们可以对其进行修改。
- 一个修改是将{(s,r,s′)}\{(s, r, s')\}{(s,r,s′)}更改为{(st,rt+1,st+1)}\{(s_t, r_{t+1}, s_{t+1})\}{(st,rt+1,st+1)},这样算法就可以利用一个回合中的顺序样本。
- 另一个修改是用它的估计值替代vπ(s′)v_\pi(s')vπ(s′),因为我们事先并不知道它。
算法的收敛性
vt+1(st)=vt(st)−αt(st)[vt(st)−[rt+1+γvt(st+1)]]v_{t+1}(s_t) = v_t(s_t) - α_t(s_t)[v_t(s_t) - [r_{t+1} + γv_t(s_{t+1})]]vt+1(st)=vt(st)−αt(st)[vt(st)−[rt+1+γvt(st+1)]]
通过TD算法(1),即上式,当t→∞t \rightarrow \inftyt→∞时,如果对所有s∈Ss \in \mathcal{S}s∈S满足∑tαt(s)=∞\sum_t \alpha_t(s) = \infty∑tαt(s)=∞且∑tαt2(s)<∞\sum_t \alpha_t^2(s) < \infty∑tαt2(s)<∞,则vt(s)v_t(s)vt(s)以概率1收敛到vπ(s)v_\pi(s)vπ(s)。
注意:
- 该定理表明对于给定的策略π\piπ,可以通过TD算法找到状态价值。
- ∑tαt(s)=∞\sum_t \alpha_t(s) = \infty∑tαt(s)=∞和∑tαt2(s)<∞\sum_t \alpha_t^2(s) < \infty∑tαt2(s)<∞必须对所有s∈Ss \in \mathcal{S}s∈S有效。在时间步ttt,如果s=sts = s_ts=st,意味着时间ttt访问了状态sss,则αt(s)>0\alpha_t(s) > 0αt(s)>0;否则,对于所有其他s≠sts \neq s_ts=st,αt(s)=0\alpha_t(s) = 0αt(s)=0。这要求每个状态必须被访问无限(或足够多)次。
- 访问状态与学习率的关系
- 在强化学习的TD算法中,学习率αt(s)\alpha_t(s)αt(s)决定了在状态sss下,基于新获得的信息(即时奖励和下一个状态的估计值)对当前状态估计值进行更新的程度。
- 当在时间步ttt访问了状态sss(即s=sts = s_ts=st)时,αt(s)>0\alpha_t(s)>0αt(s)>0,这是因为只有访问了这个状态,才能根据这个状态下的信息(如即时奖励rt+1r_{t + 1}rt+1和下一个状态的估计值vt(st+1)v_t(s_{t+1})vt(st+1))来更新该状态的估计值vt(s)v_t(s)vt(s)。如果没有访问这个状态,就没有新的信息来更新它,所以对于所有其他s≠sts\neq s_ts=st,αt(s)=0\alpha_t(s) = 0αt(s)=0。
- 状态必须被访问足够多次的原因
- 对于收敛条件∑tαt(s)=∞\sum_t\alpha_t(s)=\infty∑tαt(s)=∞和∑tαt2(s)<∞\sum_t\alpha_t^2(s)<\infty∑tαt2(s)<∞,∑tαt(s)=∞\sum_t\alpha_t(s)=\infty∑tαt(s)=∞这个条件要求对每个状态s∈Ss\in\mathcal{S}s∈S,总的学习率之和要趋近于无穷。从直观上理解,这意味着每个状态都需要被访问足够多次,以便积累足够的更新信息来使估计值能够不断调整。
- 例如,假设某个状态sss很少被访问,那么αt(s)\alpha_t(s)αt(s)只有在很少的时间步才不为零。如果这种情况持续下去,∑tαt(s)\sum_t\alpha_t(s)∑tαt(s)就不会趋近于无穷,那么这个状态的估计值vt(s)v_t(s)vt(s)就可能无法充分地根据新信息进行更新,从而无法保证收敛到真实的状态价值vπ(s)v_{\pi}(s)vπ(s)。只有当每个状态都被访问无限(或足够多)次,才能保证有足够的信息来让估计值不断地向真实值靠拢,最终实现收敛。
- 访问状态与学习率的关系
- 学习率α\alphaα通常被选择为一个小常数。在这种情况下,条件∑tαt2(s)<∞\sum_t \alpha_t^2(s) < \infty∑tαt2(s)<∞不再有效。当α\alphaα是常数时,仍然可以证明算法在期望意义上收敛。
TD learning与MC learning
MC learning:https://blog.youkuaiyun.com/Rsbstep/article/details/146240629?spm=1001.2014.3001.5502
尽管TD学习和MC学习都是无模型的,与MC学习相比,TD学习有哪些优势和劣势?
| TD/Sarsa learning | MC learning |
|---|---|
| online: TD学习是在线的。它可以在接收到奖励后立即更新状态/动作值。 | offline: MC学习是离线的。它必须等到一个回合完全收集完毕。 |
| Continuing tasks: 由于TD学习是在线的,它可以处理既有情节性任务也有持续性任务。 | Episodic tasks: 由于MC学习是离线的,它只能处理有终止状态的情节性任务。 |
尽管TD学习和MC学习都是无模型的,与MC学习相比,TD学习有哪些优势和劣势?
| TD/Sarsa learning | MC learning |
|---|---|
| bootstrap: TD是自举的,因为值的更新依赖于该值的先前估计。因此,它需要初始猜测。 | Non-bootstrapping: MC不是自举的,因为它可以直接估计状态/动作值,无需任何初始猜测。 |
| 低估计方差: TD的方差比MC低,因为它涉及的随机变量更少。例如,Sarsa只需要Rt+1R_{t+1}Rt+1,St+1S_{t+1}St+1,At+1A_{t+1}At+1。 | 高估计方差: 要估计qπ(st,at)q_\pi(s_t,a_t)qπ(st,at),我们需要Rt+1+γRt+2+γ2Rt+3+…R_{t+1} + \gamma R_{t+2} + \gamma^2 R_{t+3} + \ldotsRt+1+γRt+2+γ2Rt+3+…的样本。假设每个回合的长度为LLL,则有AL\mathcal{A}^LAL种可能的回合。 |
在强化学习中,“bootstrap”(自举)是一个技术术语,指的是一种利用估计值来更新估计值的方法。
具体来说:
- 当TD(时间差分)学习算法使用自举时,它会使用当前状态值的估计来更新另一个状态值的估计。例如,在上面的TD算法中,我们使用下一个状态的估计值V(st+1)V(s_{t+1})V(st+1)来更新当前状态的估计值V(st)V(s_t)V(st),这是一种自举方法。
- 这与MC(蒙特卡洛)方法形成对比,MC方法不使用自举,而是直接使用实际观察到的回报(从当前到终止状态的所有奖励的折现总和)来更新估计值。
- 自举可以加速学习过程,因为它允许算法在观察到完整的回报之前就开始学习,但它也可能引入偏差,特别是如果初始估计不准确的话。
- 在表格中提到TD需要"初始猜测"正是因为这个自举特性:由于每次更新都依赖于其他状态的估计值,所以需要给所有状态赋予一些初始估计值作为起点。
TD learning of action values: Sarsa
算法介绍
首先,我们的目标是估计给定策略π\piπ的动作价值。
假设我们有一些经验{(st,at,rt+1,st+1,at+1)}t\{(s_t, a_t, r_{t+1}, s_{t+1}, a_{t+1})\}_t{(st,at,rt+1,st+1,at+1)}t。
我们可以使用以下Sarsa算法来估计动作价值:
qt+1(st,at)=qt(st,at)−αt(st,at)[qt(st,at)−[rt+1+γqt(st+1,at+1)]],qt+1(s,a)=qt(s,a),∀(s,a)≠(st,at),q_{t+1}(s_t, a_t) = q_t(s_t, a_t) - \alpha_t(s_t, a_t)[q_t(s_t, a_t) - [r_{t+1} + \gamma q_t(s_{t+1}, a_{t+1})]], \\
q_{t+1}(s, a) = q_t(s, a), \quad \forall(s, a) \neq (s_t, a_t),qt+1(st,at)=qt(st,at)−αt(st,at)[qt(st,at)−[rt+1+γqt(st+1,at+1)]],qt+1(s,a)=qt(s,a),∀(s,a)=(st,at),
其中t=0,1,2,…t = 0, 1, 2, \ldotst=0,1,2,…
- qt(st,at)q_t(s_t, a_t)qt(st,at)是qπ(st,at)q_\pi(s_t, a_t)qπ(st,at)的估计;
- αt(st,at)\alpha_t(s_t, a_t)αt(st,at)是取决于st,ats_t, a_tst,at的学习率。
为什么这个算法被称为Sarsa?
这是因为算法的每一步都涉及(st,at,rt+1,st+1,at+1)(s_t, a_t, r_{t+1}, s_{t+1}, a_{t+1})(st,at,rt+1,st+1,at+1)。
Sarsa是状态-动作-奖励-状态-动作(state-action-reward-state-action)的缩写。
Sarsa与之前的TD学习算法有什么关系?
我们可以通过将TD算法中的状态价值估计v(s)v(s)v(s)替换为动作价值估计q(s,a)q(s, a)q(s,a)来得到Sarsa。
因此,Sarsa是TD算法的动作价值版本。
Sarsa算法在数学上做什么?
Sarsa的表达式表明它是一个随机近似算法,用于解决以下方程:
qπ(s,a)=E[R+γqπ(S′,A′)∣s,a],∀s,a.q_\pi(s, a) = \mathbb{E}[R + \gamma q_\pi(S', A')|s, a], \quad \forall s, a.qπ(s,a)=E[R+γqπ(S′,A′)∣s,a],∀s,a.
这是用动作价值表示的Bellman方程的另一种表达形式。
算法收敛性
通过Sarsa算法,当t→∞t \rightarrow \inftyt→∞时,如果对所有(s,a)(s, a)(s,a)满足∑tαt(s,a)=∞\sum_t \alpha_t(s, a) = \infty∑tαt(s,a)=∞和∑tαt2(s,a)<∞\sum_t \alpha_t^2(s, a) < \infty∑tαt2(s,a)<∞,则qt(s,a)q_t(s, a)qt(s,a)以概率1收敛到动作价值qπ(s,a)q_\pi(s, a)qπ(s,a)。
该定理表明可以通过Sarsa找到给定策略π\piπ的动作价值。
Sarsa的实现
强化学习的最终目标是找到最优策略。
为了实现这一目标,我们可以将Sarsa与策略改进步骤相结合。这种组合算法也被称为Sarsa。
伪代码:通过Sarsa进行策略搜索
对于每个episode,如果当前的sts_tst不是目标状态:
- 收集经验(st,at,rt+1,st+1,at+1)(s_t, a_t, r_{t+1}, s_{t+1}, a_{t+1})(st,at,rt+1,st+1,at+1):
- 按照πt(st)\pi_t(s_t)πt(st)选择动作ata_tat,生成rt+1r_{t+1}rt+1,st+1s_{t+1}st+1,
- 然后按照πt(st+1)\pi_t(s_{t+1})πt(st+1)选择动作at+1a_{t+1}at+1。
- 更新q值:
- qt+1(st,at)=qt(st,at)−αt(st,at)[qt(st,at)−[rt+1+γqt(st+1,at+1)]]q_{t+1}(s_t, a_t) = q_t(s_t, a_t) - \alpha_t(s_t, a_t)[q_t(s_t, a_t) - [r_{t+1} + \gamma q_t(s_{t+1}, a_{t+1})]]qt+1(st,at)=qt(st,at)−αt(st,at)[qt(st,at)−[rt+1+γqt(st+1,at+1)]]
- 更新策略:
- πt+1(a∣st)=1−ϵ∣A∣(∣A∣−1)\pi_{t+1}(a|s_t) = 1 - \frac{\epsilon}{|\mathcal{A}|}(|\mathcal{A}| - 1)πt+1(a∣st)=1−∣A∣ϵ(∣A∣−1) 若 a=argmaxaqt+1(st,a)a = \arg\max_a q_{t+1}(s_t, a)a=argmaxaqt+1(st,a)
- 否则πt+1(a∣st)=ϵ∣A∣\pi_{t+1}(a|s_t) = \frac{\epsilon}{|\mathcal{A}|}πt+1(a∣st)=∣A∣ϵ
关于该算法的说明:
- sts_tst的策略在q(st,at)q(s_t, a_t)q(st,at)更新后立即更新。这是基于广义策略迭代的思想。
- 策略是ϵ\epsilonϵ-贪婪而不是纯贪婪,以便很好地平衡利用与探索。
明确核心思想和复杂性:
- 核心思想很简单:即使用算法求解给定策略的Bellman方程。
- 复杂性出现在我们尝试寻找最优策略并高效工作时。
Sarsa算法的例子
任务描述:
- 任务是从特定起始状态到目标状态找到一条好的路径。
- 这个任务与之前所有需要为每个状态找出最优策略的任务不同!
- 每个回合从左上角状态开始,在目标状态结束。
- rtarget=0r_{\text{target}} = 0rtarget=0,rforbidden=rboundary=−10r_{\text{forbidden}} = r_{\text{boundary}} = -10rforbidden=rboundary=−10,且rother=−1r_{\text{other}} = -1rother=−1。学习率为α=0.1\alpha = 0.1α=0.1,ϵ\epsilonϵ的值为0.1。
结果:
- 左侧图显示了Sarsa获得的最终策略。
- 并非所有状态都有最优策略。
- 右侧图显示了每个回合的总奖励和长度。
- 每回合总奖励的指标将被频繁使用
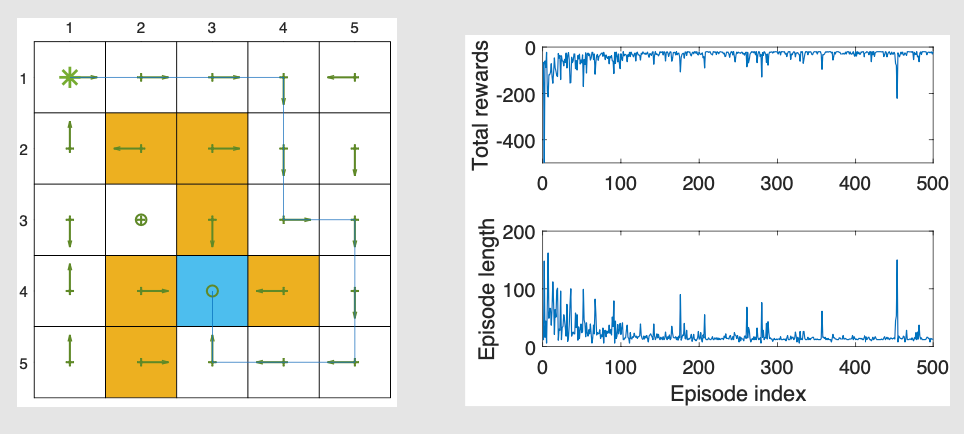
- 每回合总奖励的指标将被频繁使用
“Episode length”(回合长度)在强化学习中是指一个回合(episode)从开始到结束所经历的时间步(time steps)数量。
在上文中:
- 每个回合从起始状态(左上角)开始,到达目标状态结束
- 回合长度表示智能体从起始状态到达目标状态所需的步数
- 较短的回合长度通常意味着找到了更高效的路径
- 图中右下方显示的"Episode length"图表展示了随着训练进行,每个回合的长度变化
TD learning of action values: Expected Sarsa
Sarsa的一个变体是Expected Sarsa算法:
qt+1(st,at)=qt(st,at)−αt(st,at)[qt(st,at)−(rt+1+γE[qt(st+1,A)])],qt+1(s,a)=qt(s,a),∀(s,a)≠(st,at),q_{t+1}(s_t, a_t) = q_t(s_t, a_t) - \alpha_t(s_t, a_t)[q_t(s_t, a_t) - (r_{t+1} + \gamma\mathbb{E}[q_t(s_{t+1}, A)])], \\
q_{t+1}(s, a) = q_t(s, a), \quad \forall(s, a) \neq (s_t, a_t),qt+1(st,at)=qt(st,at)−αt(st,at)[qt(st,at)−(rt+1+γE[qt(st+1,A)])],qt+1(s,a)=qt(s,a),∀(s,a)=(st,at),
其中
E[qt(st+1,A)])=∑aπt(a∣st+1)qt(st+1,a)=vt(st+1)\mathbb{E}[q_t(s_{t+1}, A)]) = \sum_a \pi_t(a|s_{t+1})q_t(s_{t+1}, a) = v_t(s_{t+1})E[qt(st+1,A)])=a∑πt(a∣st+1)qt(st+1,a)=vt(st+1)
是在策略πt\pi_tπt下qt(st+1,a)q_t(s_{t+1}, a)qt(st+1,a)的期望值。
与Sarsa相比:
- TD目标发生了变化,从Sarsa中的rt+1+γqt(st+1,at+1)r_{t+1} + \gamma q_t(s_{t+1}, a_{t+1})rt+1+γqt(st+1,at+1)变为Expected Sarsa中的rt+1+γE[qt(st+1,A)]r_{t+1} + \gamma\mathbb{E}[q_t(s_{t+1}, A)]rt+1+γE[qt(st+1,A)]。
- 需要更多计算。但它的好处在于降低了估计方差,因为它将Sarsa中的随机变量从{st,at,rt+1,st+1,at+1}\{s_t, a_t, r_{t+1}, s_{t+1}, a_{t+1}\}{st,at,rt+1,st+1,at+1}减少到{st,at,rt+1,st+1}\{s_t, a_t, r_{t+1}, s_{t+1}\}{st,at,rt+1,st+1}。
算法的数学性分析
Expected Sarsa是一种随机近似算法,用于解决以下方程:
qπ(s,a)=E[Rt+1+γEAt+1∼π(St+1)[qπ(St+1,At+1)]∣St=s,At=a],∀s,a.q_\pi(s, a) = \mathbb{E}\left[R_{t+1} + \gamma\mathbb{E}_{A_{t+1}\sim\pi(S_{t+1})}[q_\pi(S_{t+1}, A_{t+1})]|S_t = s, A_t = a\right], \quad \forall s, a.qπ(s,a)=E[Rt+1+γEAt+1∼π(St+1)[qπ(St+1,At+1)]∣St=s,At=a],∀s,a.
上述方程是Bellman方程的另一种表达式:
qπ(s,a)=E[Rt+1+γvπ(St+1)∣St=s,At=a],q_\pi(s, a) = \mathbb{E}[R_{t+1} + \gamma v_\pi(S_{t+1})|S_t = s, A_t = a],qπ(s,a)=E[Rt+1+γvπ(St+1)∣St=s,At=a],
示例:
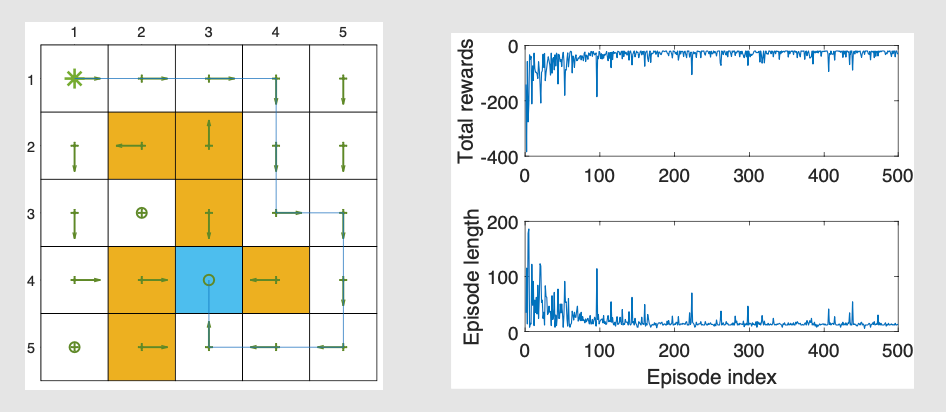
图表显示了一个5x5的网格环境,左图表示学到的策略,右上图显示了随着训练进行每个回合的总奖励,右下图显示了每个回合的长度
TD learning of action values: n-step Sarsa
n-step Sarsa:可以统一Sarsa和蒙特卡洛学习
动作价值的定义是
qπ(s,a)=E[Gt∣St=s,At=a].q_\pi(s, a) = \mathbb{E}[G_t|S_t = s, A_t = a].qπ(s,a)=E[Gt∣St=s,At=a].
折扣回报GtG_tGt可以用不同形式表示为
Sarsa⟵Gt(1)=Rt+1+γqπ(St+1,At+1),Gt(2)=Rt+1+γRt+2+γ2qπ(St+2,At+2),⋮n-step Sarsa⟵Gt(n)=Rt+1+γRt+2+⋯+γnqπ(St+n,At+n),⋮MC⟵Gt(∞)=Rt+1+γRt+2+γ2Rt+3+… \begin{align} \text{Sarsa} \longleftarrow \quad & G_t^{(1)} = R_{t+1} + \gamma q_\pi(S_{t+1}, A_{t+1}), \\ & G_t^{(2)} = R_{t+1} + \gamma R_{t+2} + \gamma^2 q_\pi(S_{t+2}, A_{t+2}), \\ & \vdots \\ \text{$n$-step Sarsa} \longleftarrow \quad & G_t^{(n)} = R_{t+1} + \gamma R_{t+2} + \cdots + \gamma^n q_\pi(S_{t+n}, A_{t+n}), \\ & \vdots \\ \text{MC} \longleftarrow \quad & G_t^{(\infty)} = R_{t+1} + \gamma R_{t+2} + \gamma^2 R_{t+3} + \ldots \end{align} Sarsa⟵n-step Sarsa⟵MC⟵Gt(1)=Rt+1+γqπ(St+1,At+1),Gt(2)=Rt+1+γRt+2+γ2qπ(St+2,At+2),⋮Gt(n)=Rt+1+γRt+2+⋯+γnqπ(St+n,At+n),⋮Gt(∞)=Rt+1+γRt+2+γ2Rt+3+…
应当注意,Gt=Gt(1)=Gt(2)=Gt(n)=Gt(∞)G_t = G_t^{(1)} = G_t^{(2)} = G_t^{(n)} = G_t^{(\infty)}Gt=Gt(1)=Gt(2)=Gt(n)=Gt(∞),其中上标仅表示GtG_tGt的不同分解结构。
-
Sarsa 旨在求解
qπ(s,a)=E[Gt(1)∣s,a]=E[Rt+1+γqπ(St+1,At+1)∣s,a].q_\pi(s, a) = \mathbb{E}[G_t^{(1)} | s, a] = \mathbb{E}[R_{t+1} + \gamma q_\pi(S_{t+1}, A_{t+1}) | s, a].qπ(s,a)=E[Gt(1)∣s,a]=E[Rt+1+γqπ(St+1,At+1)∣s,a]. -
蒙特卡洛(MC)学习旨在求解
qπ(s,a)=E[Gt(∞)∣s,a]=E[Rt+1+γRt+2+γ2Rt+3+…∣s,a].q_\pi(s, a) = \mathbb{E}[G_t^{(\infty)} | s, a] = \mathbb{E}[R_{t+1} + \gamma R_{t+2} + \gamma^2 R_{t+3} + \dots | s, a].qπ(s,a)=E[Gt(∞)∣s,a]=E[Rt+1+γRt+2+γ2Rt+3+…∣s,a]. -
一种称为 n 步 Sarsa 的中间算法旨在求解
qπ(s,a)=E[Gt(n)∣s,a]=E[Rt+1+γRt+2+⋯+γnqπ(St+n,At+n)∣s,a].q_\pi(s, a) = \mathbb{E}[G_t^{(n)} | s, a] = \mathbb{E}[R_{t+1} + \gamma R_{t+2} + \dots + \gamma^n q_\pi(S_{t+n}, A_{t+n}) | s, a].qπ(s,a)=E[Gt(n)∣s,a]=E[Rt+1+γRt+2+⋯+γnqπ(St+n,At+n)∣s,a]. -
n 步 Sarsa 的算法为
qt+1(st,at)=qt(st,at)−αt(st,at)[qt(st,at)−(rt+1+γrt+2+⋯+γnqt(st+n,at+n))] \begin{align*} q_{t+1}(s_t, a_t) &= q_t(s_t, a_t) \\ &\quad - \alpha_t(s_t, a_t) \big[ q_t(s_t, a_t) - \big( r_{t+1} + \gamma r_{t+2} + \dots + \gamma^n q_t(s_{t+n}, a_{t+n}) \big) \big] \end{align*} qt+1(st,at)=qt(st,at)−αt(st,at)[qt(st,at)−(rt+1+γrt+2+⋯+γnqt(st+n,at+n))]
n 步 Sarsa 更具一般性,因为当n=1n = 1n=1 时,它变为(单步)Sarsa 算法;当n=∞n = \inftyn=∞ 时,它变为蒙特卡洛学习算法。 -
n步Sarsa需要(st,at,rt+1,st+1,at+1,…,rt+n,st+n,at+n)(s_t, a_t, r_{t+1}, s_{t+1}, a_{t+1}, \dots, r_{t+n}, s_{t+n}, a_{t+n})(st,at,rt+1,st+1,at+1,…,rt+n,st+n,at+n)。
-
由于在时刻ttt时,(rt+n,st+n,at+n)(r_{t+n}, s_{t+n}, a_{t+n})(rt+n,st+n,at+n)还未被收集,我们无法在步骤ttt执行n步Sarsa。然而,我们可以等到时刻t+nt+nt+n来更新(st,at)(s_t, a_t)(st,at)的q值:
qt+n(st,at)=qt+n−1(st,at)−αt+n−1(st,at)[qt+n−1(st,at)−(rt+1+γrt+2+⋯+γnqt+n−1(st+n,at+n))] \begin{align*} q_{t+n}(s_t, a_t) &= q_{t+n-1}(s_t, a_t) \\ &- \alpha_{t+n-1}(s_t, a_t) \big[ q_{t+n-1}(s_t, a_t) - \big( r_{t+1} + \gamma r_{t+2} + \cdots + \gamma^n q_{t+n-1}(s_{t+n}, a_{t+n}) \big) \big] \end{align*} qt+n(st,at)=qt+n−1(st,at)−αt+n−1(st,at)[qt+n−1(st,at)−(rt+1+γrt+2+⋯+γnqt+n−1(st+n,at+n))] -
由于n步Sarsa包含Sarsa和蒙特卡洛学习这两种极端情况,其性能是Sarsa和蒙特卡洛学习的混合:
-
如果nnn较大,其性能接近蒙特卡洛学习,因此有大的方差但偏差小。
-
如果nnn较小,其性能接近Sarsa,因此由于初始猜测会有相对大的偏差,且方差相对低。
-
最后,n步Sarsa也用于策略评估。它可以与策略改进步骤结合以搜索最优策略。




















 591
591

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








