强化学习-Chapter8-价值函数的近似法&DQN

例子：曲线拟合

迄今为止，状态值与动作值均通过表格表示。

• 例如，动作值：

	$a_1$	$a_2$	$a_3$	$a_4$	$a_5$
$s_1$	$q_{\pi }(s_1,a_1)$	$q_{\pi }(s_1,a_2)$	$q_{\pi }(s_1,a_3)$	$q_{\pi }(s_1,a_4)$	$q_{\pi }(s_1,a_5)$
$⋮$	$⋮$	$⋮$	$⋮$	$⋮$	$⋮$
$s_9$	$q_{\pi }(s_9,a_1)$	$q_{\pi }(s_9,a_2)$	$q_{\pi }(s_9,a_3)$	$q_{\pi }(s_9,a_4)$	$q_{\pi }(s_9,a_5)$

• 优点：直观且易于分析
• 缺点：难以处理大规模或连续的状态空间或动作空间。体现在两个方面：1）存储；2）泛化能力

考虑一个例子：

• 假设存在一维状态 $s_1,\dots ,s_{|\mathcal{S}|}$。
• 它们的状态值为 $v_{\pi }(s_1),\dots ,v_{\pi }(s_{|\mathcal{S}|})$，其中 $\pi$ 是给定的策略。
• 假设 $|\mathcal{S}|$ 非常大，且我们希望使用一条简单的曲线来近似这些点，以节省存储空间。
  
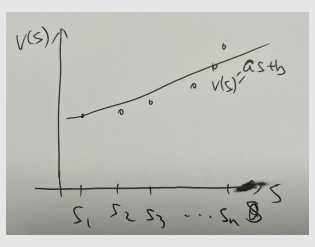
  首先，我们使用最简单的直线来拟合这些点。
  假设直线方程为
  $$\hat{v}(s,w)=as+b=\underset{{\varphi }^T(s)}{\underbrace{[s,1]}}\underset{w}{\underbrace{\left[\begin{array}{c}a\\ b\end{array}\right]}}={\varphi }^T(s)w$$
  其中：
• $w$ 是 parameter vector（参数向量）
• $\varphi (s)$ 是 $s$ 的 feature vector（特征向量）
• $\hat{v}(s,w)$ 在 $w$ 上是线性的

这样做的好处如下：

• 表格表示需要存储 $|\mathcal{S}|$ 个状态值。而现在，我们只需存储两个参数 $a$ 和 $b$。
• 每当我们想使用状态 $s$ 的值时，都可以通过计算 ${\varphi }^T(s)w$ 得到。
• 这种好处并非没有代价。它伴随的成本是：状态值无法被精确表示。这就是为什么该方法被称为值函数近似。

其次，我们也可以使用二阶曲线来拟合这些点：
$$\hat{v}(s,w)=a{s}^2+bs+c=\underset{{\varphi }^T(s)}{\underbrace{[s^2,s,1]}}\underset{w}{\underbrace{\left[\begin{array}{c}a\\ b\\ c\end{array}\right]}}={\varphi }^T(s)w.$$
在这种情况下：

• $w$ 和 $\varphi (s)$ 的维度增加了，但值可能会拟合得更精确。
• 尽管 $\hat{v}(s,w)$ 在 $s$ 上是非线性的，但它在 $w$ 上是线性的。非线性包含在 $\varphi (s)$ 中。

第三，我们甚至可以使用更高阶的多项式曲线或其他复杂曲线来拟合这些点。

• 优点：能够更好地进行近似。
• 缺点：需要更多的参数。

总结:

• 核心思想：使用参数化函数近似状态值与动作值：$\hat{v}(s,w)\approx v_{\pi }(s)$，其中 $w\in {\mathbb{R}}^m$ 是参数向量。
• 关键区别：如何获取与设定 $v(s)$ 的值。
• 优点：
  • 存储：$w$ 的维度可能远小于 $|\mathcal{S}|$。
  • 泛化性：当某个状态 $s$ 被访问时，参数 $w$ 会更新，从而使其他未被访问状态的值也能得到更新。

状态值估计的算法

目标函数

以更正式的方式介绍：

• 令 $v_{\pi }(s)$ 和 $\hat{v}(s,w)$ 分别为真实状态值与用于近似的函数。
• 我们的目标是找到一个 最优 的 $w$，使得对于每个 $s$，$\hat{v}(s,w)$ 都能最佳地近似 $v_{\pi }(s)$。
• 这是一个策略评估问题。后续我们会将其扩展到策略改进。
• 为找到最优的 $w$，我们需要 两个步骤：
  • 第一步是定义一个目标函数。
  • 第二步是推导优化目标函数的算法。

目标函数为
$$J(w)=\mathbb{E}[(v_{\pi }(S)-\hat{v}(S,w){)}^2].$$

• 公式组成
  • $v_{\pi }(S)$：真实状态值函数，表示在策略 $\pi$ 下，状态 $S$ 的真实长期回报期望。
  • $\hat{v}(S,w)$：近似值函数，通过参数化函数（如线性模型、神经网络）对真实值函数的拟合结果，$w$ 是模型参数。
  • $(v_{\pi }(S)-\hat{v}(S,w){)}^2$：单个状态 $S$ 上，真实值与近似值的平方误差，衡量局部拟合误差。
  • $\mathbb{E}[\cdot ]$：数学期望，对状态 $S$ 的概率分布求平均，确保整体误差最小化。
• 目标意义
  • 该函数通过最小化真实值与近似值的 均方误差期望，寻找最优参数 $w$。本质是让近似函数 $\hat{v}(S,w)$ 在统计意义上尽可能贴近真实值函数 $v_{\pi }(S)$，平衡所有状态上的拟合效果，而非仅关注个别状态。
  • 例如，在线性回归中类似最小二乘法目标，此处扩展到强化学习的状态值近似场景，通过优化 $w$ 提升值函数近似的准确性。
• 这里的期望是关于随机变量 $S\in \mathcal{S}$ 的。那么 $S$ 的概率分布是什么？
  有多种方式可以定义 $S$ 的概率分布。

方式一：均匀分布

第一种方法是使用均匀分布。

• 即通过将每个状态的概率设为 $1/|\mathcal{S}|$，将所有状态视为同等重要。
• 在这种情况下，目标函数变为：
  $$J(w)=\mathbb{E}[(v_{\pi }(S)-\hat{v}(S,w){)}^2]=\frac{1}{|\mathcal{S}|}\sum _{s\in \mathcal{S}}(v_{\pi }(s)-\hat{v}(s,w){)}^2.$$
• 缺点：
  • 状态的重要性可能并不相同。例如，某些状态可能在策略中极少被访问。因此，这种方法没有考虑给定策略下马尔可夫过程的真实动态。

方式二：平稳分布

第二种方法是使用平稳分布。
平稳分布是一个重要概念，简而言之，它描述了马尔可夫过程的长期行为。

马尔可夫过程（Markov Process），又称马尔可夫链，是满足马尔可夫性质的随机过程
语言描述为：“未来状态仅依赖当前状态，与过去状态无关”
数学表示为：对状态序列$s_1,s_2,\dots ,s_t,s_{t+1}$，有$P(s_{t+1}\mid s_t)=P(s_{t+1}\mid s_1,s_2,\cdots ,s_t)$

• 令 {dπ(s)}s∈S\{d_\pi(s)\}_{s \in \mathcal{S}}{dπ​(s)}s∈S​ 表示策略 $\pi$ 下马尔可夫过程的平稳分布。根据定义，$d_{\pi }(s)\ge 0$ 且 ${\sum }_{s\in \mathcal{S}}{d}_{\pi }(s)=1$。
• 目标函数可改写为：
  $J(w)=\mathbb{E}[(v_{\pi }(S)-\hat{v}(S,w){)}^2]={\sum }_{s\in \mathcal{S}}{d}_{\pi }(s)(v_{\pi }(s)-\hat{v}(s,w){)}^2$。
  该函数是一个加权平方误差。
• 由于被访问更频繁的状态具有更高的 $d_{\pi }(s)$ 值，它们在目标函数中的权重也比那些很少被访问的状态更高。

关于平稳分布的更多解释：

• 平稳分布也被称为 稳态分布 或 极限分布
• Distribution（分布）：状态的分布
• Stationary（平稳）：长期行为
• 总结：智能体遵循某一策略运行很长时间后，处于任意状态的概率都可以用该分布描述。

举例说明：

• 给定图中所示的一个策略。
• 令 $n_{\pi }(s)$ 表示在策略 $\pi$ 下一个很长的episode 中，状态 $s$ 被访问的次数。
• 那么，$d_{\pi }(s)$ 可通过下式近似：
  $$d_{\pi }(s)\approx \frac{n_{\pi }(s)}{{\sum }_{s^{\prime }\in \mathcal{S}}{n}_{\pi }(s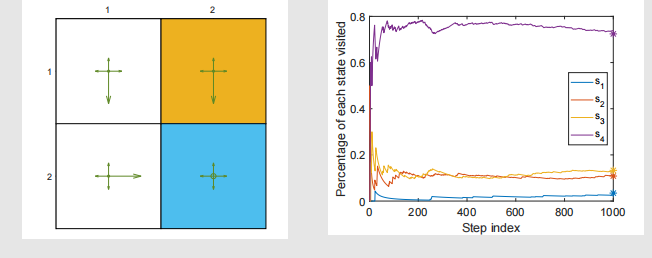^{\prime })}$$
  收敛值是可以预测的，因为它们是 $d_{\pi }$ 的元素：
  $$d_{\pi }^T=d_{\pi }^T{P}_{\pi }$$
• 直观理解为：经过一次状态转移（由 $P_{\pi }$ 描述）后，状态分布不变。
• 数学本质：该公式等价于求矩阵 $P_{\pi }$ 特征值为 $1$ 的左特征向量，因为 $d_{\pi }^T{P}_{\pi }=1\cdot d_{\pi }^T$，这里 $1$ 是特征值，$d_{\pi }^T$ 是对应的左特征向量。

对于这个例子，我们有 $P_{\pi }$ 如下：
$$P_{\pi }=\left[\begin{array}{cccc}0.3& 0.1& 0.6& 0\\ 0.1& 0.3& 0& 0.6\\ 0.1& 0& 0.3& 0.6\\ 0& 0.1& 0.1& 0.8\end{array}\right]$$
$P_{\pi }$ 是策略 $\pi$ 下的状态转移矩阵，每一行表示从某个状态出发，转移到其他状态的概率。例如：

• 第一行 $[0.3,0.1,0.6,0]$ 表示从第 1 个状态出发，转移到第 1、2、3、4 个状态的概率分别是 $0.3$、$0.1$、$0.6$、$0$。

可以计算出，对应特征值为 $1$ 的左特征向量是：
$$d_{\pi }={\left[\begin{array}{c}0.0345,0.1084,0.1330,0.7241\end{array}\right]}^T$$
得到平稳分布 $d_{\pi }$。每个元素表示长期运行后，系统处于对应状态的概率。例如 $0.7241$ 表示处于第 4 个状态的概率最高，反映了策略 $\pi$ 下状态的长期分布特性。

最优化算法

既然我们已经有了目标函数，下一步就是对其进行优化。

为了最小化目标函数 $J(w)$，我们可以使用梯度下降算法：
$$w_{k+1}=w_k-{\alpha }_k{\nabla }_{w}J(w_k)$$
真实的梯度为：
$$\begin{array}{rl}{\nabla }_{w}J(w)& ={\nabla }_w\mathbb{E}[(v_{\pi }(S)-\hat{v}(S,w){)}^2]\\ & =\mathbb{E}[{\nabla }_w(v_{\pi }(S)-\hat{v}(S,w){)}^2]\\ & =2\mathbb{E}[(v_{\pi }(S)-\hat{v}(S,w))(-{\nabla }_w\hat{v}(S,w))]\\ & =-2\mathbb{E}[(v_{\pi }(S)-\hat{v}(S,w)){\nabla }_w\hat{v}(S,w)]\end{array}$$
上述真实梯度涉及期望的计算。但是我们可以使用随机梯度来代替真实梯度：
$$w_{t+1}=w_t+{\alpha }_t(v_{\pi }(s_t)-\hat{v}(s_t,w_t)){\nabla }_w\hat{v}(s_t,w_t),$$
其中 $s_t$ 是 $S$ 的一个样本。此处，将 $2{\alpha }_k$ 合并到 ${\alpha }_k$ 中。

• 此算法不可实现，因为它需要真实状态值 $v_{\pi }$，而这是待估计的未知量。
• 我们可以用一个近似值替换 $v_{\pi }(s_t)$，以使算法可实现。

有两种近似值替换方式：

• 第一，带函数近似的蒙特卡洛学习
  令 $g_t$ 为此回合中从状态 $s_t$ 开始的折扣回报。那么，$g_t$ 可用于近似 $v_{\pi }(s_t)$。算法变为：
  $$w_{t+1}=w_t+{\alpha }_t(g_t-\hat{v}(s_t,w_t)){\nabla }_w\hat{v}(s_t,w_t).$$
• 第二，带函数近似的时序差分学习
  依据时序差分学习的思想，$r_{t+1}+\gamma \hat{v}(s_{t+1},w_t)$ 可被视为 $v_{\pi }(s_t)$ 的近似。然后，算法变为：
  $$w_{t+1}=w_t+{\alpha }_t[r_{t+1}+\gamma \hat{v}(s_{t+1},w_t)-\hat{v}(s_t,w_t)]{\nabla }_w\hat{v}(s_t,w_t).$$

伪代码：
以带函数近似的时序差分学习为例
初始化：一个关于 $w$ 可微的函数 $\hat{v}(s,w)$，初始参数 $w_0$。
目标：近似给定策略 $\pi$ 的真实状态值。
对遵循策略 $\pi$ 的每个episode，执行：
  对每个step $(s_t,r_{t+1},s_{t+1})$，执行：
    一般情况下，
      $w_{t+1}=w_t+{\alpha }_t[r_{t+1}+\gamma \hat{v}(s_{t+1},w_t)-\hat{v}(s_t,w_t)]{\nabla }_w\hat{v}(s_t,w_t)$
    线性情况下，
      由于$\hat{v}(s,w)={\varphi }^T(s)w$，${\nabla }_w\hat{v}(s_t,w_t)=\varphi (s_t)$
      那么：
      $w_{t+1}=w_t+{\alpha }_t[r_{t+1}+\gamma {\varphi }^T(s_{t+1})w_t-{\varphi }^T(s_t)w_t]\varphi (s_t)$
它只能估计给定策略的状态值，但理解它对后续介绍的其他算法很重要。

函数近似器的选择

一个尚未解答的重要问题：如何选择函数 $\hat{v}(s,w)$？

• 第一种方法，过去被广泛使用，是使用线性函数
  $$\hat{v}(s,w)={\varphi }^T(s)w$$
  这里，$\varphi (s)$ 是特征向量，它可以是多项式基、傅里叶基……。我们在引例中已见过，后续的说明性示例中还会再次见到。
• 第二种方法，如今被广泛使用，是使用神经网络作为非线性函数近似器。
  神经网络的输入是状态s，输出是状态值$\hat{v}(s,w)$，网络参数是 $w$。

在线性情形下，$\hat{v}(s,w)={\varphi }^T(s)w$，我们有
$${\nabla }_w\hat{v}(s,w)=\varphi (s).$$
将该梯度代入 TD 算法
$$w_{t+1}=w_t+{\alpha }_t[r_{t+1}+\gamma \hat{v}(s_{t+1},w_t)-\hat{v}(s_t,w_t)]{\nabla }_w\hat{v}(s_t,w_t)$$
得到
$$w_{t+1}=w_t+{\alpha }_t[r_{t+1}+\gamma {\varphi }^T(s_{t+1})w_t-{\varphi }^T(s_t)w_t]\varphi (s_t),$$
这就是带线性函数近似的 TD 学习算法。简称为 TD-Linear。

• 线性函数近似的缺点：
  • 难以选择合适的特征向量。
• 线性函数近似的优点：
  • 与非线性情形相比，线性情形下 TD 算法的理论性质更容易被理解。
  • 线性函数近似仍然强大，因为表格表示仅仅是线性函数近似的一种特殊情况。

我们接下来展示，表格表示是线性函数近似的一种特殊情况。

• 首先，考虑状态 $s$ 的特殊特征向量：
  $$\varphi (s)=e_s\in {\mathbb{R}}^{|\mathcal{S}|},$$
  其中 $e_s$ 是一个向量，其第 $s$ 个元素为 $1$，其余元素为 $0$。
• 在这种情况下，
  $$\hat{v}(s,w)=e_s^{T}w=w(s),$$
  其中 $w(s)$ 是 $w$ 的第 $s$ 个元素。

回忆一下，TD-Linear算法为：
$$w_{t+1}=w_t+{\alpha }_t[r_{t+1}+\gamma {\varphi }^T(s_{t+1})w_t-{\varphi }^T(s_t)w_t]\varphi (s_t),$$

• 当 $\varphi (s_t)=e_s$ 时，上述算法变为：
  $$w_{t+1}=w_t+{\alpha }_t(r_{t+1}+\gamma w_t(s_{t+1})-w_t(s_t))e_{s_t}.$$
  这是一个向量方程，仅更新 $w_t$ 的第 $s_t$ 个元素。
• 在方程两边乘以 $e_{s_t}^T$ 可得：
  $$w_{t+1}(s_t)=w_t(s_t)+{\alpha }_t(r_{t+1}+\gamma w_t(s_{t+1})-w_t(s_t)),$$
  这恰好是表格型TD算法。

说明性示例

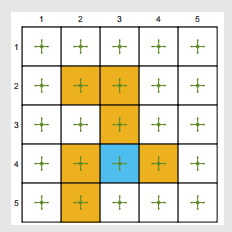
考虑一个 5×5 网格世界示例：

• 给定一个策略：对任意的状态 $s$ 和动作 $a$，有 $\pi (a|s)=0.2$。
• 我们的目标是估计该策略的状态值（策略评估问题）。
• 总共有 25 个状态值。接下来我们将展示，能够使用少于 25 个参数来近似这些状态值。
• 设置 $r_{\text{forbidden}}=r_{\text{boundary}}=-1$，$r_{\text{target}}=1$，且 $\gamma =0.9$。
  

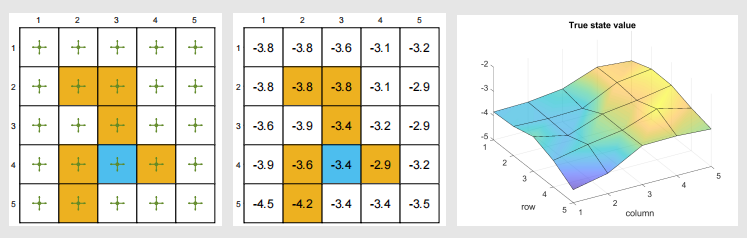
真实情况：

• 真实状态值及三维可视化
  

经验样本：

• 遵循给定策略生成了 500 个episode。
• 每个episode有 500 步，且从均匀分布随机选择的状态-动作对开始。

为便于对比，此处展示表格型 TD 算法（简称为 TD-Table）得出的结果。

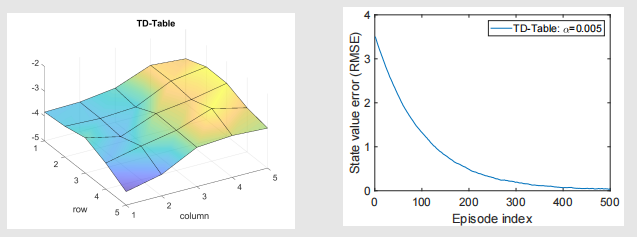
接下来我们展示 TD-Linear 算法的结果。
特征向量选择：
$$\varphi (s)=\left[\begin{array}{c}1\\ x\\ y\end{array}\right]\in {\mathbb{R}}^3.$$
在这种情况下，近似状态值为：
$$\hat{v}(s,w)={\varphi }^T(s)w=[1,x,y]\left[\begin{array}{c}{w}_1\\ w_2\\ w_3\end{array}\right]=w_1+w_{2}x+w_{3}y.$$
值得注意的是，$\varphi (s)$也可定义为 $\varphi (s)=[x,y,1{]}^T$，其中元素顺序无关紧要。

为增强近似能力，我们可以使用 高阶特征向量，进而使用更多参数。

• 例如，我们可以考虑
  $$\varphi (s)=[1,x,y,x^2,y^2,xy{]}^T\in {\mathbb{R}}^6.$$
  在这种情况下，
  $$\hat{v}(s,w)={\varphi }^T(s)w=w_1+w_{2}x+w_{3}y+w_4{x}^2+w_5{y}^2+w_{6}xy$$
  这对应一个二次曲面。
• 我们可以进一步增加特征向量的维度：
  $$\varphi (s)=[1,x,y,x^2,y^2,xy,x^3,y^3,x^{2}y,x{y}^2{]}^T\in {\mathbb{R}}^{10}.$$

使用高阶特征向量的 TD-Linear 算法结果：

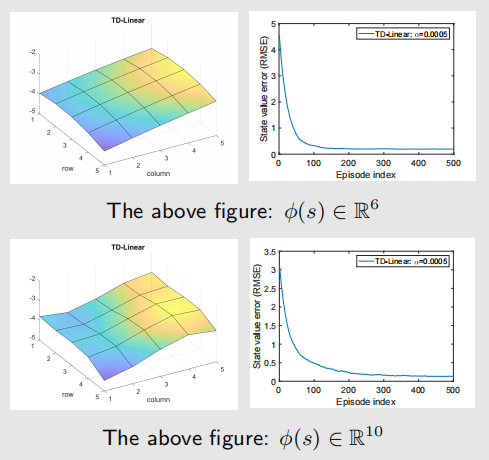
总结

1. 从目标函数开始：
   $$J(w)=\mathbb{E}[(v_{\pi }(S)-\hat{v}(S,w){)}^2].$$
   该目标函数表明这是一个策略评估问题。
2. 梯度下降算法为：
   $$w_{t+1}=w_t+{\alpha }_t(v_{\pi }(s_t)-\hat{v}(s_t,w_t)){\nabla }_w\hat{v}(s_t,w_t),$$
3. 算法中未知的真实值函数被近似值替代，得到以下算法：
   $$w_{t+1}=w_t+{\alpha }_t[r_{t+1}+\gamma \hat{v}(s_{t+1},w_t)-\hat{v}(s_t,w_t)]{\nabla }_w\hat{v}(s_t,w_t).$$
   尽管这部分内容有助于理解基本思想，但它在数学上并不严谨。

理论分析

• 算法
  $$w_{t+1}=w_t+{\alpha }_t[r_{t+1}+\gamma \hat{v}(s_{t+1},w_t)-\hat{v}(s_t,w_t)]{\nabla }_w\hat{v}(s_t,w_t)$$
  不会最小化以下目标函数：
  $$J(w)=\mathbb{E}[(v_{\pi }(S)-\hat{v}(S,w){)}^2]$$
  主要原因如下：
• 目标函数与更新逻辑的偏差：
  • 若要最小化 $J(w)$，需基于真实值 $v_{\pi }(S)$ 计算梯度。理想梯度下降更新应为：
    $$w_{t+1}=w_t+{\alpha }_t\mathbb{E}\left[(v_{\pi }(s_t)-\hat{v}(s_t,w_t)){\nabla }_w\hat{v}(s_t,w_t)\right]$$
  • 但实际算法中，$v_{\pi }(s_t)$ 未知，只能用 $r_{t+1}+\gamma \hat{v}(s_{t+1},w_t)$ 近似替代。这种近似使得更新方向不再严格对应 $J(w)$ 的梯度，无法保证最小化 $J(w)$。
• 算法本质关联的误差类型：
  • 该 TD 算法更贴近优化 贝尔曼误差（如 $J_{BE}(w)$），而非直接最小化真实值误差 $J(w)$。
  • 贝尔曼误差（Bellman Error）反映值函数近似结果与理论上贝尔曼方程解的偏差，而 $J(w)$ 关注近似值与真实值的直接差距。
  • 两者目标不同，导致算法更新逻辑不服务于 $J(w)$ 的最小化。

不同的目标函数：

• 目标函数 1：真实值误差
  $$J_E(w)=\mathbb{E}[(v_{\pi }(S)-\hat{v}(S,w){)}^2]=\Vert \hat{v}(w)-v_{\pi }{\Vert }_D^2$$

• 目标函数 2：贝尔曼误差
  $$J_{BE}(w)=\Vert \hat{v}(w)-(r_{\pi }+\gamma P_{\pi }\hat{v}(w)){\Vert }_D^2\doteq \Vert \hat{v}(w)-T_{\pi }(\hat{v}(w)){\Vert }_D^2,$$
  其中 $T_{\pi }(x)\doteq r_{\pi }+\gamma P_{\pi }x$是贝尔曼算子，$r_{\pi }$ 是策略 $\pi$ 下的期望回报，$P_{\pi }$ 是状态转移概率，$\Vert \cdot {\Vert }_D^2$ 表示基于状态分布 $D$ 的加权范数。

• 目标函数 3：投影贝尔曼误差
  $$J_{PBE}(w)=\Vert \hat{v}(w)-M{T}_{\pi }(\hat{v}(w)){\Vert }_D^2,$$
  其中 $M$ 是一个投影矩阵。
  TD-Linear 算法会最小化投影贝尔曼误差。

带有函数近似值的 Sarsa

到目前为止，我们仅仅考虑了状态值估计的问题。也就是说，我们希望$\hat{v}\approx v_{\pi }$

为了寻找最优策略，我们需要估计动作值。

公式

带值函数近似的Sarsa算法的形式是：

$w_{t+1}=w_t+{\alpha }_t\left[r_{t+1}+\gamma \hat{q}(s_{t+1},a_{t+1},w_t)-\hat{q}(s_t,a_t,w_t)\right]{\nabla }_w\hat{q}(s_t,a_t,w_t).$

• 公式拆解
  • 权重更新规则
    • $w_{t+1}$：下一时刻的参数（权重）向量
    • $w_t$：当前时刻的参数向量。
    • ${\alpha }_t$：学习率（步长），控制更新幅度。
  • 时间差分（TD）误差
    • $r_{t+1}$：从状态$s_t$执行动作$a_t$后获得的即时奖励。
    • $\gamma$：折扣因子，体现未来奖励的重要性。
    • $\hat{q}(s_{t+1},a_{t+1},w_t)$：下一状态$s_{t+1}$执行动作$a_{t+1}$的估计Q值（基于当前参数$w_t$）。
    • $\hat{q}(s_t,a_t,w_t)$：当前状态$s_t$执行动作$a_t$的估计Q值。
    • TD误差：$r_{t+1}+\gamma \hat{q}(s_{t+1},a_{t+1},w_t)-\hat{q}(s_t,a_t,w_t)$，表示预测值与目标值的差异。
  • 梯度方向
    • ${\nabla }_w\hat{q}(s_t,a_t,w_t)$：Q函数关于参数$w_t$的梯度向量
• 核心思想
  • 目标：通过调整参数$w$，使$\hat{q}(s,a,w)$更准确地估计真实Q值。
  • TD学习：利用当前奖励和下一状态的Q值估计，逐步修正当前状态的Q值（类似Q-learning的单步更新）。
  • 梯度优化：通过梯度方向调整参数，直接优化TD误差的平方（即最小化$(r_{t+1}+\gamma {\hat{q}}_{t+1}-{\hat{q}}_t{)}^2$）。

伪代码

为了寻找最优策略，我们可以结合策略评估和策略改进。
伪代码：带函数近似的Sarsa与

目标：搜索一个策略，能够从初始状态-动作对$(s_0,a_0)$引导智能体到达目标。

• 对于每个回合，执行
  • 如果当前$s_t$不是目标状态，执行
    • 根据${\pi }_t(s_t)$选择动作$a_t$，生成$r_{t+1},s_{t+1}$，然后根据${\pi }_t(s_{t+1})$选择动作$a_{t+1}$
    • 值更新（参数更新）：$w_{t+1}=w_t+{\alpha }_t\left[r_{t+1}+\gamma \hat{q}(s_{t+1},a_{t+1},w_t)-\hat{q}(s_t,a_t,w_t)\right]{\nabla }_w\hat{q}(s_t,a_t,w_t)$
    • 策略更新：
      ${\pi }_{t+1}(a|s_t)=1-\frac{\epsilon }{|\mathcal{A}(s)|}(|\mathcal{A}(s)|-1)$ 如果 $a=\arg {\max }_{a\in \mathcal{A}(s_t)}\hat{q}(s_t,a,w_{t+1})$
      否则${\pi }_{t+1}(a|s_t)=\frac{\epsilon }{|\mathcal{A}(s)|}$

示例说明

带线性函数近似的Sarsa：
$\gamma =0.9$, $ϵ=0.1$, $r_{\text{boundary}}=r_{\text{forbidden}}=-10$, $r_{\text{target}}=1$, $\alpha =0.001$。

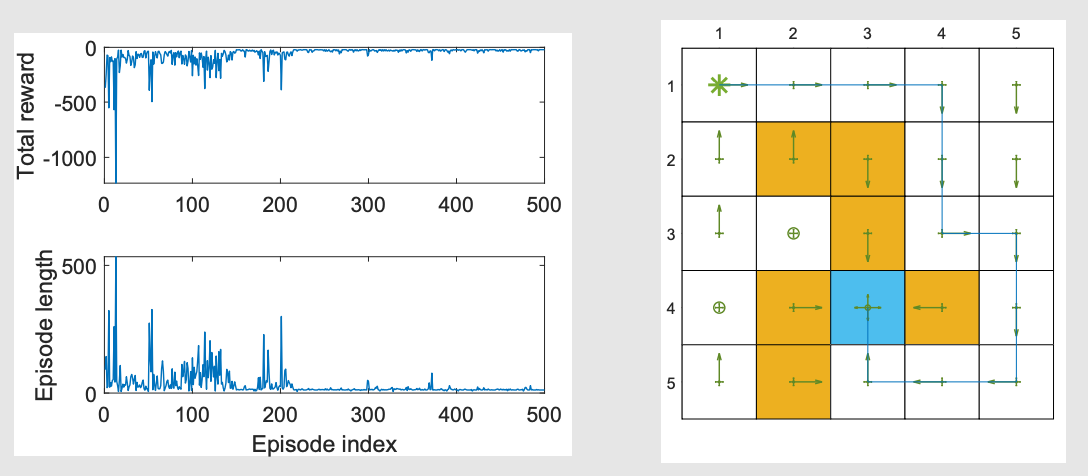
带函数近似的Q-learning

公式

与Sarsa类似，表格式Q-learning也可以扩展到值函数近似的情况。

q值更新规则为

$$w_{t+1}=w_t+{\alpha }_t\left[r_{t+1}+\gamma \underset{a\in \mathcal{A}(s_{t+1})}{\max }\hat{q}(s_{t+1},a,w_t)-\hat{q}(s_t,a_t,w_t)\right]{\nabla }_w\hat{q}(s_t,a_t,w_t),$$

这与Sarsa相同，只是$\hat{q}(s_{t+1},a_{t+1},w_t)$被${\max }_{a\in \mathcal{A}(s_{t+1})}\hat{q}(s_{t+1},a,w_t)$所替代。

伪代码

伪代码：带函数近似的Q-learning（on-policy版本）

初始化：初始参数向量$w_0$。初始策略${\pi }_0$。小$\epsilon >0$。
目标：搜索一个良好的策略，使智能体能从初始状态-动作对$(s_0,a_0)$到达目标。
对于每个回合，执行

• 如果当前$s_t$不是目标状态，执行
  • 按照${\pi }_t(s_t)$采取动作$a_t$，并生成$r_{t+1},s_{t+1}$值更新（参数更新）：
    $w_{t+1}=w_t+{\alpha }_t\left[r_{t+1}+\gamma {\max }_{a\in \mathcal{A}(s_{t+1})}\hat{q}(s_{t+1},a,w_t)-\hat{q}(s_t,a_t,w_t)\right]{\nabla }_w\hat{q}(s_t,a_t,w_t)$
  • 策略更新：
    ${\pi }_{t+1}(a|s_t)=1-\frac{\epsilon }{|\mathcal{A}(s)|}(|\mathcal{A}(s)|-1)$ 如果 $a=\arg {\max }_{a\in \mathcal{A}(s_t)}\hat{q}(s_t,a,w_{t+1})$
    否则${\pi }_{t+1}(a|s_t)=\frac{\epsilon }{|\mathcal{A}(s)|}$

示例说明

带线性函数近似的Q-learning
$\gamma =0.9$，$ϵ=0.1$，$r_{\text{boundary}}=r_{\text{forbidden}}=-10$，$r_{\text{target}}=1$，$\alpha =0.001$。

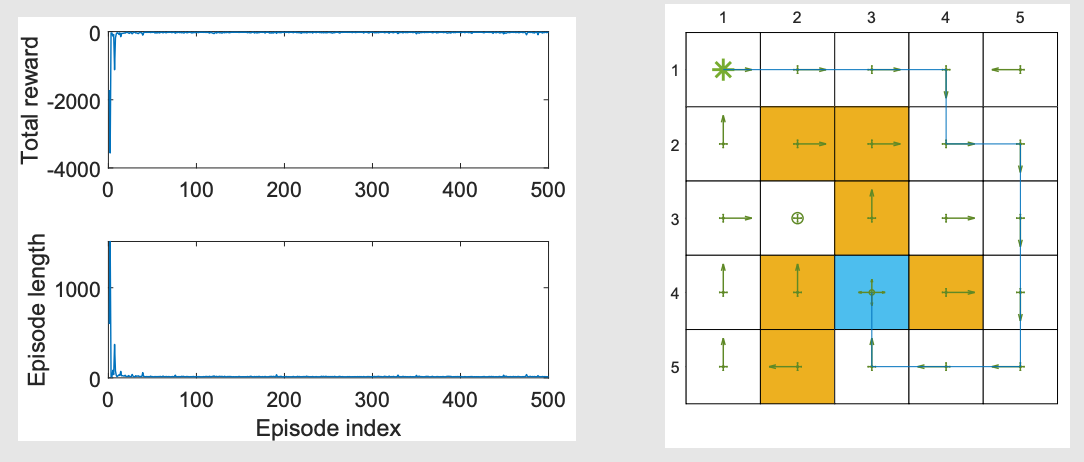
Deep Q-learning（DQN）

DQN算法思想

Deep Q-learning 或 deep Q-network (DQN)：

• 最早且最成功的将深度神经网络引入强化学习(RL)的算法之一。
• 神经网络的作用是作为非线性函数近似器。

DQN是一种用于解决强化学习问题的深度学习算法，它的核心是学习一个Q - 函数（动作价值函数）。这个Q - 函数$\hat{q}(S,A,w)$以状态$S$、动作$A$和参数$w$作为输入，输出一个估计的价值，表示在状态$S$下采取动作$A$的长期回报。

目标函数

DQN旨在最小化目标函数/损失函数：
$$J(w)=\mathbb{E}\left[{\left(R+\gamma \underset{a\in \mathcal{A}(S^{\prime })}{\max }\hat{q}(S^{\prime },a,w)-\hat{q}(S,A,w)\right)}^2\right],$$
其中$(S,A,R,S^{\prime })$是随机变量。

• 这里$\mathbb{E}$表示数学期望，它是对所有可能的状态转换$(S,A,R,S^{\prime })$求平均。其中$S$是当前状态，$A$是在状态$S$下采取的动作，$R$是获得的即时奖励，$S^{\prime }$是下一个状态。

• $\gamma$是折扣因子，通常取值在$0$到$1$之间，用于衡量未来奖励的重要性。$\hat{q}(S^{\prime },a,w)$是在下一个状态$S^{\prime }$下采取动作$a$的Q - 值估计，${\max }_{a\in \mathcal{A}(S^{\prime })}\hat{q}(S^{\prime },a,w)$表示在下一个状态$S^{\prime }$下采取最优动作的Q - 值估计。

• 这实际上是Bellman最优性误差。这是因为

  • Bellman方程
    $$q(s,a)=\mathbb{E}\left[R_{t+1}+\gamma \underset{a\in \mathcal{A}(S_{t+1})}{\max }q(S_{t+1},a)\mid S_t=s,A_t=a\right]$$是强化学习中的一个基本方程。它描述了状态 - 动作价值函数$q(s,a)$的递归关系。
    • 简单来说，在状态$s$下采取动作$a$的价值等于立即获得的奖励$R_{t+1}$加上未来状态下采取最优动作的折扣价值$\gamma {\max }_{a\in \mathcal{A}(S_{t+1})}q(S_{t+1},a)$的期望。
  • 与目标函数的联系
    • 在理想情况下，我们希望估计的Q - 函数$\hat{q}(S,A,w)$能够满足Bellman方程。
    • 也就是说，
      • 从期望的角度来看，$R+\gamma {\max }_{a\in \mathcal{A}(S^{\prime })}\hat{q}(S^{\prime },a,w)-\hat{q}(S,A,w)$的值应该为零。
      • 这是因为如果我们的估计是准确的，那么根据Bellman方程，即时奖励加上下一个状态的最优Q - 值估计（经过折扣）应该等于当前状态 - 动作对的Q - 值估计。
    • 而实际中，由于我们的估计$\hat{q}$可能不准确，所以这个差值不为零
      • 这个差值的平方的期望$J(w)$就是我们要最小化的目标函数，这个差值也被称为Bellman最优性误差。
      • 通过最小化这个目标函数，我们可以让DQN学习到更准确的Q - 函数估计。

公式拆解

如何最小化目标函数？梯度下降！
如何计算目标函数的梯度？很棘手！

• 这是因为，在这个目标函数
  $$J(w)=\mathbb{E}\left[{\left(R+\gamma \underset{a\in \mathcal{A}(S^{\prime })}{\max }\hat{q}(S^{\prime },a,w)-\hat{q}(S,A,w)\right)}^2\right],$$
  参数$w$不仅出现在$\hat{q}(S,A,w)$中，还出现在
  $$y\doteq R+\gamma \underset{a\in \mathcal{A}(S^{\prime })}{\max }\hat{q}(S^{\prime },a,w)$$
• 为了简化，我们可以假设在计算梯度时，$y$中的$w$是固定的（至少暂时固定）。

为了实现这一点，我们可以引入两个网络。

• 一个是主网络，表示$\hat{q}(s,a,w)$
• 另一个是目标网络，$\hat{q}(s,a,w_T)$。

在这种情况下，目标函数简化为
$$J=\mathbb{E}\left[{\left(R+\gamma \underset{a\in \mathcal{A}(S^{\prime })}{\max }\hat{q}(S^{\prime },a,w_T)-\hat{q}(S,A,w)\right)}^2\right],$$
其中$w_T$是目标网络参数。

当$w_T$固定时，$J$的梯度可以容易地得到为
$${\nabla }_{w}J=\mathbb{E}\left[2\left(R+\gamma \underset{a\in \mathcal{A}(S^{\prime })}{\max }\hat{q}(S^{\prime },a,w_T)-\hat{q}(S,A,w)\right)(-{\nabla }_w\hat{q}(S,A,w))\right]$$

• 在实际应用中，通常会忽略常数 $2$（因为在优化过程中，乘以一个常数不影响梯度的方向）
• 负号也可以忽略因为：
  • 在基于梯度的优化算法（如随机梯度下降及其变体）中，我们关注的是梯度的方向。忽略掉负号，梯度的方向只是从下降变为上升，但这并不影响优化过程的本质。
  • 无论是梯度上升还是梯度下降，我们的目的都是通过沿着某个方向更新参数，使得目标函数达到最优值（在这种情况下是最小化损失函数$J$）。
  • 当我们有梯度${\nabla }_{w}J=\mathbb{E}\left[\left(R+\gamma {\max }_{a\in \mathcal{A}(S^{\prime })}\hat{q}(S^{\prime },a,w_T)-\hat{q}(S,A,w)\right)(-{\nabla }_w\hat{q}(S,A,w))\right]$时，传统的梯度下降更新规则是$w=w-\alpha {\nabla }_{w}J$（其中$\alpha$是学习率）。
  • 如果我们忽略负号，更新规则可以写成$w=w+\alpha \mathbb{E}\left[\left(R+\gamma {\max }_{a\in \mathcal{A}(S^{\prime })}\hat{q}(S^{\prime },a,w_T)-\hat{q}(S,A,w)\right){\nabla }_w\hat{q}(S,A,w)\right]$。

因此最终得到的梯度是：
$${\nabla }_{w}J=\mathbb{E}\left[\left(R+\gamma \underset{a\in \mathcal{A}(S^{\prime })}{\max }\hat{q}(S^{\prime },a,w_T)-\hat{q}(S,A,w)\right){\nabla }_w\hat{q}(S,A,w)\right].$$

• DQN的基本思想是使用梯度下降算法来最小化目标函数。
• 然而，这种优化过程涉及一些值得特别注意的重要技术。

两个网络

第一种技术：

• 两个网络，一个主网络和一个目标网络。

为什么使用它？

• 当我们计算梯度时已经解释了数学原因。

实现细节：

• 让$w$和$w_T$分别表示主网络和目标网络的参数。它们最初被设置为相同的值。
• 在每次迭代中，我们从经验回放缓冲区（稍后将解释）中抽取一个小批量样本$\{(s,a,r,s^{\prime })\}$。
• 网络的输入包括状态$s$和动作$a$。目标输出是$y_T\doteq r+\gamma {\max }_{a\in \mathcal{A}(s^{\prime })}\hat{q}(s^{\prime },a,w_T)$。然后，我们直接最小化TD误差或称为损失函数$(y_T-\hat{q}(s,a,w){)}^2$，对小批量$\{(s,a,y_T)\}$进行优化。

经验回放

另一种技术：

• 经验回放

问题：什么是经验回放？
回答：

• 在收集了一些经验样本后，我们不按照它们被收集的顺序使用这些样本。
• 相反，我们将它们存储在一个集合中，称为回放缓冲区$\mathcal{B}=\{(s,a,r,s^{\prime })\}$
• 每次训练神经网络时，我们可以从回放缓冲区中抽取一个随机样本的小批量。
• 样本的抽取，或称为经验回放，应该遵循均匀分布（为什么？）。

问题：为什么经验回放在DQN中是必要的？为什么回放必须遵循均匀分布？
回答：答案在于目标函数。
$$J=\mathbb{E}\left[{\left(R+\gamma \underset{a\in \mathcal{A}(S^{\prime })}{\max }\hat{q}(S^{\prime },a,w)-\hat{q}(S,A,w)\right)}^2\right]$$

• $(S,A)\sim d$：$(S,A)$是一个索引，被视为单个随机变量
• $R\sim p(R|S,A),S^{\prime }\sim p(S^{\prime }|S,A)$：$R$和$S^{\prime }$由系统模型决定。
• 状态-动作对$(S,A)$的分布被假设为均匀分布。
• 然而，样本并非均匀收集，因为它们是由特定策略连续生成的。
• 为了打破连续样本之间的相关性，我们可以使用经验回放技术，从回放缓冲区中均匀抽取样本。
• 这就是经验回放必要的数学原因，以及为什么经验回放必须是均匀的。

重新审视离散表格情况：

• 问题：为什么表格式Q-learning不需要经验回放？
  • 回答：没有均匀分布要求。
    • 在表格式Q - learning中，状态 - 动作空间是离散且有限的。
    • 每次更新Q值是基于当前状态 - 动作对以及下一个状态的即时奖励和估计的未来奖励。
    • 它直接根据当前遇到的状态 - 动作对来更新Q - 表中的值。
    • 例如，假设我们有一个简单的网格世界环境，智能体可以向上、向下、向左、向右移动。Q - 表的大小是由状态数量和动作数量决定的，如状态有$m$个，动作有$n$个，Q - 表大小就是$m\times n$。当智能体在某个状态$s$采取动作$a$后，直接根据贝尔曼方程$Q(s,a)=Q(s,a)+\alpha (r+\gamma {\max }_{a^{\prime }}Q(s^{\prime },a^{\prime })-Q(s,a))$进行更新，这里并不需要从一个分布中采样数据，因为它可以精确地针对每一个状态 - 动作对进行更新，而不需要考虑数据的分布是否均匀。
• 问题：为什么deep Q-learning涉及分布？
  • 回答：深度情况下的目标函数是对所有$(S,A)$的标量平均。表格情况不涉及$S$或$A$的任何分布。表格情况下的算法旨在为所有$(s,a)$解决一组方程（贝尔曼最优性方程）。
• 问题：我们可以在表格式Q学习中使用经验回放吗？
  • 回答：是的，我们可以。而且样本效率更高（为什么？）
    • 首先，在表格式Q - learning中使用经验回放是可行的。当使用经验回放时，智能体可以存储之前的经验（状态、动作、奖励、下一个状态），并在后续的训练过程中重新利用这些经验。这样做的好处是可以打破训练数据的相关性。在没有经验回放的情况下，连续的训练样本可能是高度相关的，因为智能体的行动是连续的，这可能导致学习过程出现偏差。例如，智能体可能会陷入一个局部最优的行为模式中，因为它一直基于相似的连续经验进行学习。
    • 而样本效率更高的原因是，通过重新利用之前的经验，智能体可以在有限的训练步骤内获得更多关于环境的信息。在表格式Q - learning中，状态 - 动作空间是有限的，经验回放可以让智能体多次回顾那些比较“罕见”或者“重要”的经验。例如，在一个迷宫环境中，智能体可能只有少数几次能够到达某个关键位置并获得高奖励，通过经验回放，可以多次使用这些关键经验来更新Q - 表，从而更快地学习到正确的策略，提高样本的利用效率。

伪代码：Deep Q-learning（off-policy版本）

• 目标：从行为策略${\pi }_b$生成的经验样本中学习一个最优目标网络来近似最优动作值。
• 1.初始化：
  • 初始化深度 Q - 网络（DQN），这个网络用于近似估计 Q 值（动作价值函数）。
    • 网络的输入是环境状态 s，输出是每个可能动作的 Q 值估计 $Q(s,a)$。
  • 同时，初始化目标网络（Target Network），它的结构和 DQN 相同。
    • 目标网络用于计算目标 Q 值
    • 在训练过程中，目标网络的参数更新频率比 DQN 低，这有助于提高训练的稳定性。
  • 初始时，目标网络的参数和 DQN 的参数相同。
• 2.与环境交互
  • 将${\pi }_b$生成的经验样本存储在回放缓冲区$B=(s,a,r,s^{\prime })$
• 3.对于每次迭代，执行：
  • 训练网络（从经验回放缓冲区中采样）
    • 当经验回放缓冲区中的经验数量达到一定数量后，开始从缓冲区中随机采样一批经验数据，假设这批数据包含 k 个经验元组，即 $\{(s_i,a_i,r_i,s_{i+1}){\}}_{i=1}^k$。
    • 对于每个采样的经验元组
      • 使用 DQN 网络计算当前状态 $s_i$ 下执行动作 $a_i$ 的 Q 值估计 $\hat{q}(S,A,w)$。
      • 使用目标网络计算目标 Q 值 $y_i$。
        • 计算方式为：如果 $s_{i+1}$ 是终止状态，那么 $y_i=r_i$；
        • 如果 $s_{i+1}$ 不是终止状态，$y_T=R+\gamma {\max }_{a\in \mathcal{A}(S^{\prime })}\hat{q}(S^{\prime },a,w_T)$
          • 其中 $\gamma$ 是折扣因子（通常取值在 0 到 1 之间，用于权衡即时奖励和未来奖励的重要性）
          • $\hat{q}(S^{\prime },a,w_T)$ 是目标网络输出的 q值。
      • 根据 Q 值估计和目标 Q 值计算损失函数$(y_T-\hat{q}(s,a,w){)}^2$，最小化损失函数后得到新的$w$
  • 4.更新目标网络
    • 每隔一定的训练步骤（例如，每 C 步），将 DQN 网络的参数复制到目标网络中，使得目标网络的参数能够跟上 DQN 网络参数的更新，同时保持一定的延迟，以提高训练的稳定性。
• 重复步骤 2 - 4，直到满足训练结束条件，比如达到最大训练步数、智能体在环境中的性能达到一定标准（如平均奖励达到某个阈值）等

问题：

• 为什么没有策略更新？
  • 在 Deep Q - learning 中，虽然没有显式的策略更新步骤，但实际上策略是隐式更新的。具体原因如下：
    • 基于动作值函数的策略：Deep Q - learning 的核心是学习最优动作值函数$\hat{q}(s,a;w)$。一旦我们得到了近似的最优动作值函数，策略就可以直接从动作值函数中得到，即$\pi (s)=\arg {\max }_a\hat{q}(s,a;w)$。也就是说，只要我们不断更新动作值函数的参数$w$，策略会随着动作值函数的更新而隐式更新。简化算法流程：显式的策略更新通常会增加算法的复杂度。通过
    • 直接学习动作值函数，我们可以避免复杂的策略更新过程，使算法更加简洁和易于实现。而且，在离散动作空间中，基于动作值函数选择动作是一种非常直观和有效的方法。
• 为什么不使用我们推导的策略更新方程？
  • 算法类型差异：Deep Q - learning 是一种基于价值的算法，它的重点是学习最优动作值函数。而基于策略梯度的算法是直接对策略进行优化。两种算法的出发点和优化目标不同。基于价值的算法通过学习动作值函数来间接得到策略，而基于策略梯度的算法直接优化策略的参数。

说明性示例

说明性示例：

• 该示例旨在为每个状态-动作对学习最优动作值。
• 一旦获得最优动作值，就可以立即得到最优贪婪策略。

设置：

• 使用单个回合来训练网络。
• 这个回合是由下图所示的探索性行为策略生成的。
• 该回合仅有1,000步！table Q-learning需要100,000步。
• 使用具有单个隐藏层的浅层神经网络作为的$\hat{q}(s,a;w)$非线性近似器。隐藏层有100个神经元。
  
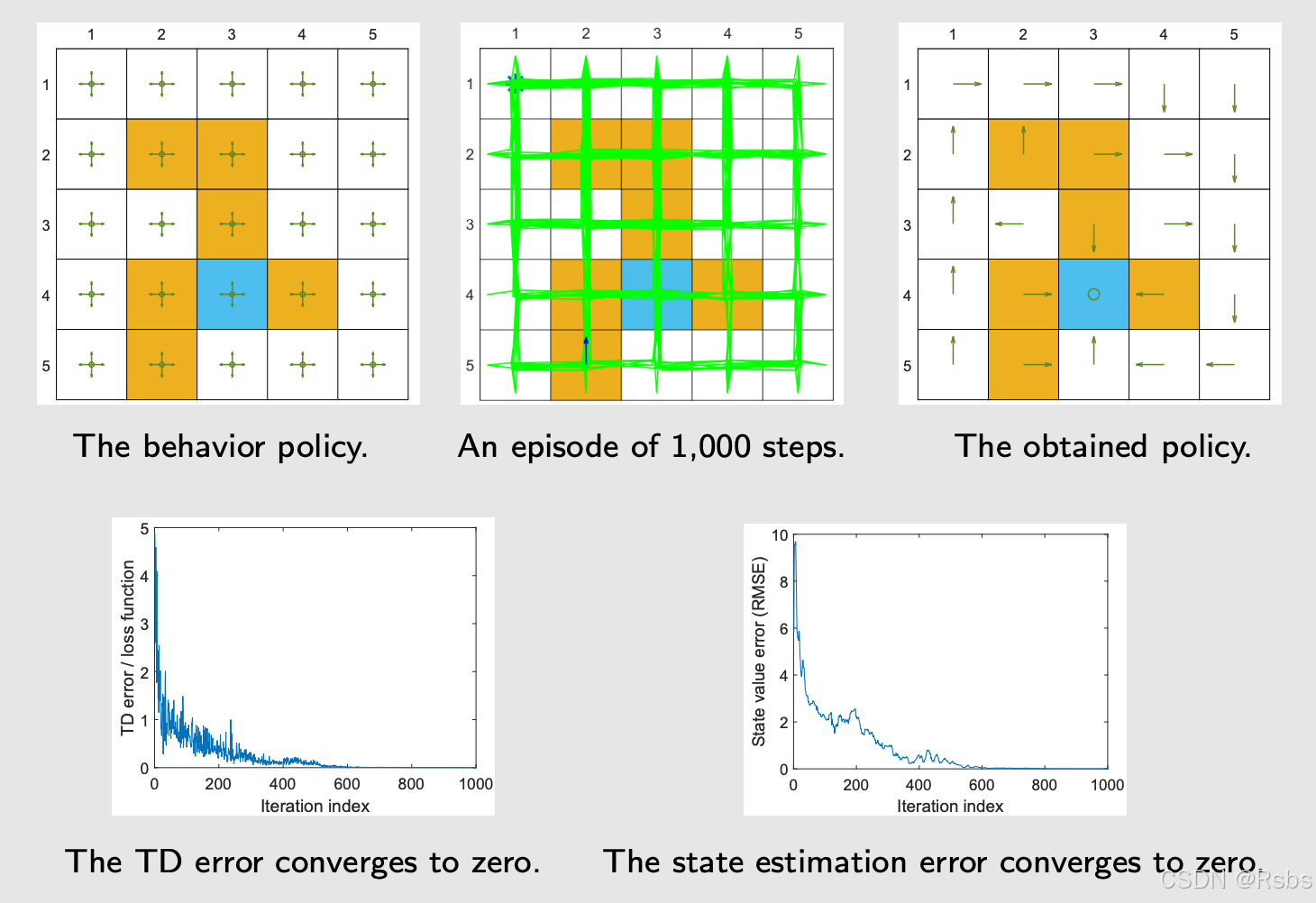
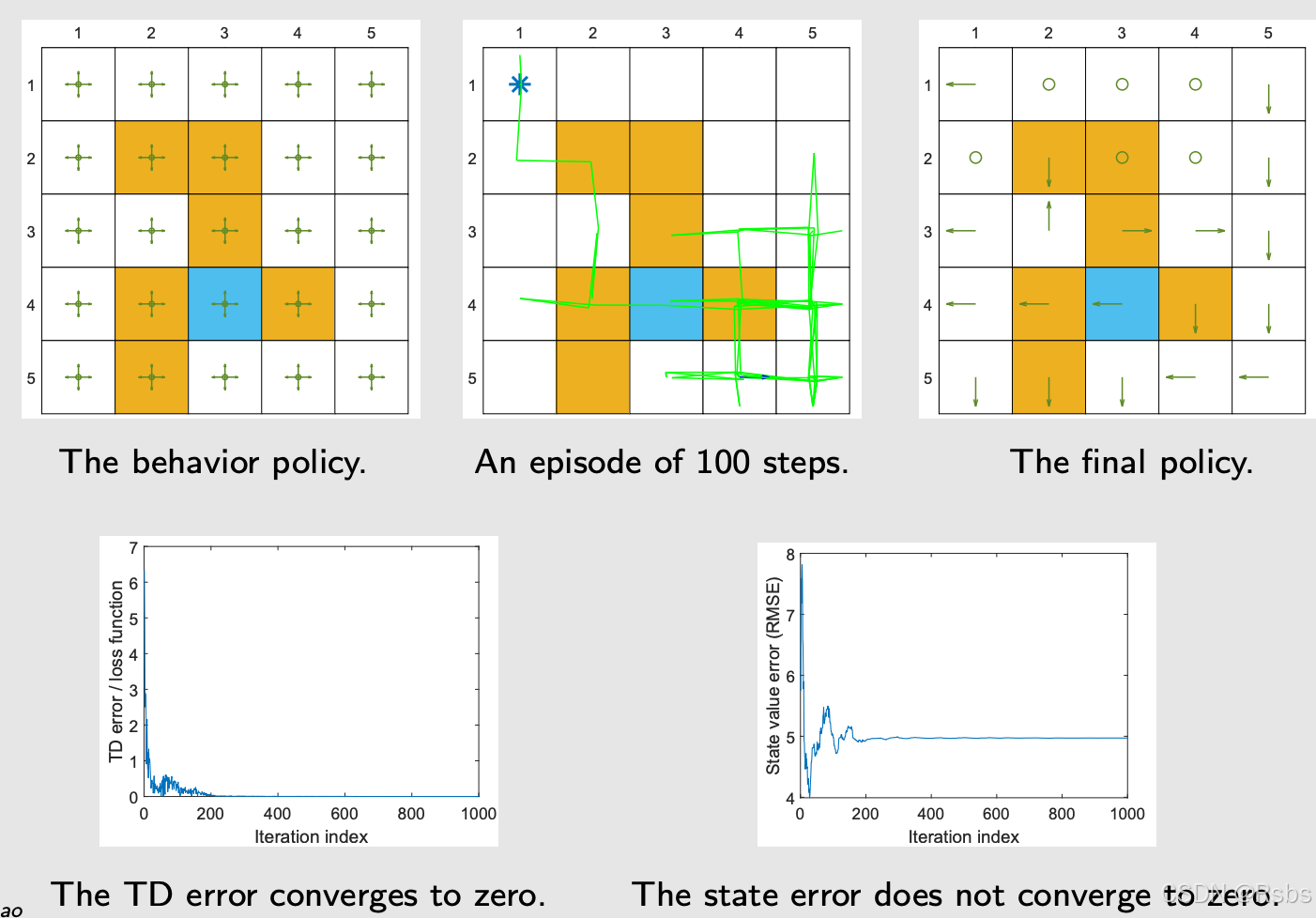
  如果我们一个回合仅100呢？那么会导致数据获取不充分。如下图所示
  

DQN & DDQN & Dueling DQN对比

对比维度	DQN	DDQN	Dueling DQN
核心网络结构	单个Q网络，输入状态，输出各动作Q值	两个Q网络（评估网络、目标网络），结构相同参数独立	单个Q网络，内部包含价值流（标量）和优势流（向量）分支，最终组合为Q值
目标网络	有，定期同步评估网络参数	有，同DQN，但目标值计算时动作选自评估网络，Q值来自目标网络	有，网络结构与DQN/DDQN一致，仅内部分支结构不同
目标值计算	$y=r+\gamma {\max }_a{Q}^{\prime }(s^{\prime },a;{\theta }^{-})$ （直接用目标网络选动作并评估）	$y=r+\gamma Q^{\prime }(s^{\prime },\arg {\max }_{a}Q(s^{\prime },a;\theta );{\theta }^{-})$ （动作选自评估网络，Q值来自目标网络）	同DDQN（目标值计算逻辑相同，仅网络内部结构不同）
网络输出层	全连接层直接输出动作数维度的Q值向量	与DQN相同	两个分支： 1. 价值流 $V(s)$（1维标量） 2. 优势流 $A(s,a)$（动作数维度向量） 最终 $Q=V+(A-\text{mean}(A))$（消除优势函数基线影响）
经验回放	使用，缓解数据相关性	使用，同DQN	使用，同DQN
损失函数	均方误差（MSE）： $L=\mathbb{E}[(y-Q(s,a;\theta ){)}^2]$	与DQN相同（仅目标值计算方式不同）	与DQN相同（仅网络输出结构不同）
动作选择策略	ε-贪心策略，基于评估网络Q值	同DQN	同DQN
参数更新方式	异步更新（评估网络定期更新目标网络）	同DQN	同DQN
关键改进点	固定目标网络+经验回放	双网络解耦动作选择与评估，减少过估计	分解Q值为状态价值和动作优势，提升状态特征利用效率
代码实现差异	基础框架，单网络结构	需维护两个网络实例，目标值计算时需显式调用评估网络选动作、目标网络算Q值	需在网络类中实现价值/优势分支，组合输出Q值，需处理优势函数均值归一化
适用动作空间	离散动作空间（输出维度=动作数）	同DQN	同DQN（优势流维度需匹配动作数）
超参数敏感点	目标网络更新频率、回放缓冲区大小	目标网络同步方式（硬更新/软更新）	优势流与价值流的权重平衡（通常直接相加）、优势函数归一化
网络输入	状态（如图像、数值向量）	同DQN	同DQN
激活函数	常用ReLU、LeakyReLU	同DQN	同DQN
优化器	Adam、RMSprop等	同DQN	同DQN
是否处理动作相关性	否（直接输出各动作Q值）	否（仅改进目标值计算）	是（通过优势流显式建模动作相对价值）

相同点总结：

1. 核心机制：均使用经验回放、目标网络、ε-贪心策略、MSE损失函数。
2. 动作空间：均针对离散动作空间设计（输出维度等于动作数量）。
3. 基础组件：输入处理、优化器选择、激活函数等工程实现基本一致。

不同点总结：

• DDQN：通过双网络分离“动作选择”和“动作评估”，目标值计算时用评估网络选动作、目标网络评估Q值，避免过估计。
• Dueling DQN：改造网络结构为价值-优势分支，显式建模状态价值和动作相对优势，提升状态特征利用效率，尤其适合状态价值主导的场景。
• 网络输出：Dueling DQN需通过公式组合价值流和优势流输出Q值，DDQN需维护两个网络实例，DQN结构最简单。