[51nod1355][数论][min-max容斥]斐波那契的最小公倍数

最新推荐文章于 2019-07-02 17:00:41 发布

原创最新推荐文章于 2019-07-02 17:00:41 发布 · 359 阅读

0 ·

CC 4.0 BY-SA版权

数论同时被 3 个专栏收录

63 篇文章

订阅专栏

51nod

11 篇文章

订阅专栏

min-max容斥

2 篇文章

订阅专栏

本文探讨了如何求解斐波那契数列中多个数的最小公倍数，并通过模运算处理大数值问题。介绍了利用斐波那契数列的特殊性质，结合容斥原理和快速幂算法，设计了一种高效算法。

Description

斐波那契数列定义如下：
F(0) = 0 F(1) = 1
F(n) = F(n-1) + F(n-2)
给出n个正整数a1, a2,… an，求对应的斐波那契数的最小公倍数，由于数字很大，输出Mod 1000000007的结果即可。
例如：1 3 6 9, 对应的斐波那契数为：1 2 8 34, 他们的最小公倍数为136。
收起

Input

第1行：1个数N，表示数字的数量（2 <= N <= 50000）。
第2 至 N + 1行：每行1个数，对应ai。（1 <= ai <= 1000000)。

Output

输出Lcm(F(a1), F(a2) … F(an)) Mod 1000000007的结果。

Sample Input

4
1
3
6
9

Sample Output

136

题解

这题实在是…有点东西
~~高一的我比初三的Cold_chair都菜这么多了玩个啥哦呜呜呜…~~
先放一下主要在哪里看的吧
milkyyyyy
Cmd2001
先看上面那个再看下面那个综合一下会舒适很多
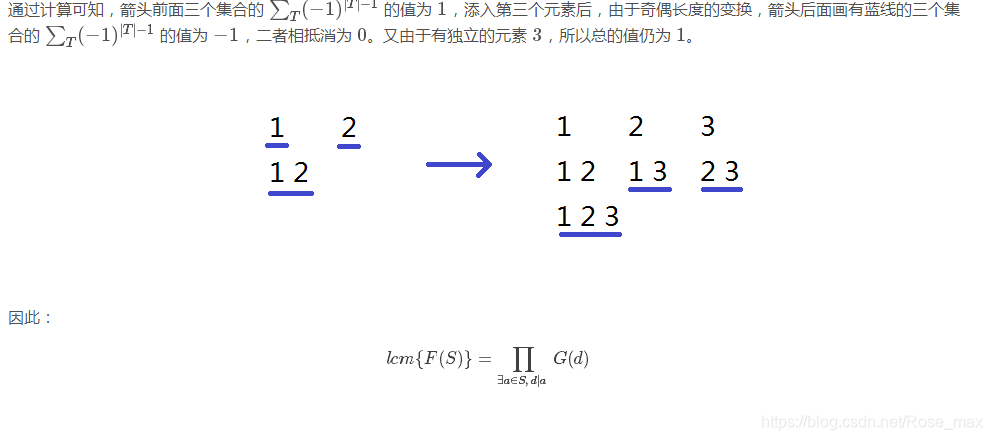
先要知道这个性质 $g c d (F (a), F (b)) = F (g c d (a, b))$ ，不会的可以看看这里
知道了又怎么样呢我们要求 $l c m$ 又不是 $g c d$ …
我们考虑一下指数在 $l c m$ 和 $g c d$ 的贡献，发现在 $l c m$ 中指数是取max，然而 $g c d$ 中指数是取min
不难想到一下min-max容斥
具体看一下上面第一篇blog吧~~不想抄了~~
有
$lcm\{S\}=\Pi_{\{T\in S\},|T|>0}gcd\{T\}^{(-1)^{|T|-1}}$
然后后面…
~~我还是想直接抄了…~~

转化完了之后，我们就要考虑怎么求这个G了
我们可以定义一下这个G为
$G(i)=F(i)*\Pi_{j|i,j!=i}G(j)^{-1}$
容易发现这样满足上面构造需求的限制
那直接 $n l o g n$ 筛就好了…

#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<algorithm>
#include<cmath>
#include<queue>
#include<vector>
#include<ctime>
#include<map>
#include<bitset>
#include<set>
#define LL long long
#define mp(x,y) make_pair(x,y)
#define pll pair<long long,long long>
#define pii pair<int,int>
using namespace std;
inline int read()
{
	int f=1,x=0;char ch=getchar();
	while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
	while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
	return x*f;
}
int stack[20];
inline void write(LL x)
{
	if(x<0){putchar('-');x=-x;}
    if(!x){putchar('0');return;}
    int top=0;
    while(x)stack[++top]=x%10,x/=10;
    while(top)putchar(stack[top--]+'0');
}
inline void pr1(int x){write(x);putchar(' ');}
inline void pr2(LL x){write(x);putchar('\n');}
const LL mod=1e9+7;
const int MAXN=1000005;
LL pow_mod(LL a,LL b)
{
	LL ret=1;
	while(b)
	{
		if(b&1)ret=ret*a%mod;
		a=a*a%mod;b>>=1;
	}
	return ret;
}
LL f[MAXN],g[MAXN];int n;
int vis[MAXN];
int main()
{
	n=read();
	f[1]=g[1]=1;
	for(int i=2;i<=MAXN-5;i++)f[i]=g[i]=(f[i-1]+f[i-2])%mod;
	for(int i=1;i<=MAXN-5;i++)
	{
		LL inv=pow_mod(g[i],mod-2);
		for(int j=2;i*j<=MAXN-5;j++)g[i*j]=g[i*j]*inv%mod;
	}
	
	for(int i=1;i<=n;i++)vis[read()]=1;
	LL ans=1;
	for(int i=1;i<=MAXN-5;i++)
	{
		for(int j=1;i*j<=MAXN-5;j++)if(vis[i*j]){ans=ans*g[i]%mod;break;}
	}
	pr2(ans);
	return 0;
}