LIFT： Learned Invariant Feature Transform 论文解读

LIFT: Learned Invariant Feature Transform

论文概述

• 创新点
  • 使用统一的模型进行端到端的有监督训练
  • 利用了传统特征提取的先验知识
• 方法
  • 训练过程

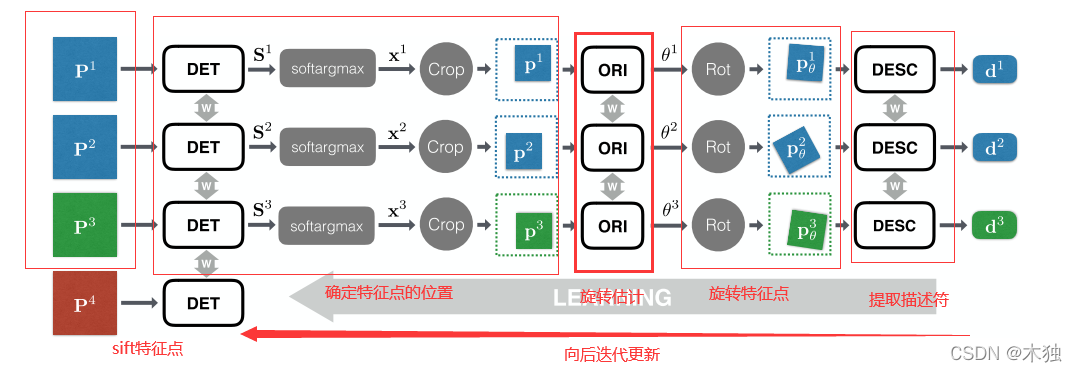
* 分阶段训练
  * 利用SfM中sift的位置和角度，训练描述符网络
  * 利用SfM中sift的位置，和训练好的描述符网络，训练旋转估计网络
  * 利用已经训练好的旋转估计和描述符网络训练特征点提取网络
* 损失函数
  * 同一个3d点的角度尽可能近
  * 匹配点描述符距离尽可能近，非匹配点尽可能远
  * 匹配点的位置比较接近
  * 非特征点位置得分尽量低

• 特征提取过程
  

• 实验验证

  • 在一些传统数据集上进行了匹配重复率测试

详细描述

简介

• 传统的手工特征点在许多计算机视觉任务中得到了广泛的应用，如三维重建，SLAM、图片检索、物体识别等等。

• 深度学习在许多计算机视觉领域取得了颠覆性的成果，在很多领域都远超传统的方法。但是在特征点提取匹配上的研究却不多。

• 现有的研究成果大多是分离，包括一些特征点提取方法，和描述子计算方法

  • 特征点提取方法
    • 很少，非深度学习方法
  • 描述子计算方法
    • Discriminative Learning of Deep Convolutional Feature Point Descriptors.
    • 描述子的学习主要在于难负样本挖掘

• 本文提出如下统一的结构，进行特征点提取匹配工作。
  
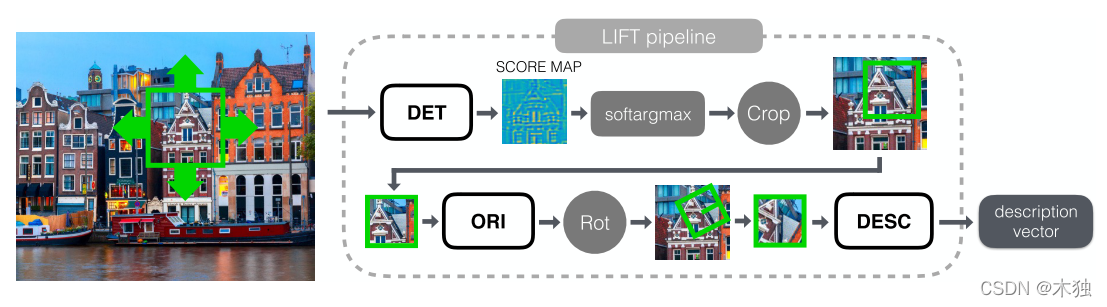
  主要难点：

• 如何保证整体的可微性

  • 将非极大值抑制替换为 soft argmax function
  • 利用特殊变换层对图片进行旋转和裁剪等操作

• 如何训练整个网络

  • 整个网络端到端的训练不可行
  • 利用SfM产生真实值以及训练特征点
    • 先训练描述子网络
    • 再训练旋转估计网络
    • 最后训练特征点提取网络

• 实际应用

  • 将所有网络解耦，在图像金字塔中使用特征点提取网络
  • 非极大值抑制得到特征点
  • 旋转估计和描述子网络均应用在提取得到的特征点上

---

因此，本文的贡献点有：

• 第一个完整的集成特征点提取、旋转估计、描述子计算深度学习端到端的架构
  • 难点，如何保证整体网络的可导
• 网络训练方法
  • 利用SfM得到patch真实值
  • 分阶段、分任务进行训练

方法

问题描述

• 采用图像patch作为输入而非整体图片作为输入进行训练，这保证了网络能够在不同尺度大小的图片上进行工作。
• 采用SfM中提取的特征点构造图片patch进行训练，每次训练采用四个patch同时输入
  • P1, P2 为同一个特征点的不同视角下的图片patch
  • P3为不同特征点对应的图片patch
  • P4为随机选取的图片patch其中不包含特征点

因此每次训练创建四个共享参数的网络对四个patch进行处理

• 包括如下部分
  • 特征点提取网络
  • softargmax 层，提取得到特征点位置（假设只有一个特征点）
  • 特殊变换层，将patch进行一定的裁剪
  • 旋转估计网络，得到角度
  • 特殊变换层2，根据角度将patch进行一定的旋转变换
  • 描述符计算层
• 其中，p4仅用来训练特征提取网络，因此没有后面的层

训练集创建

• 现有的数据集大多都用传统的特征点提取patch然后训练描述子，但是没有训练特征点的方法
• 为了获取不同视角下同一个点的patch，采用SfM方法，基于sift特征点
• 3384张图片，得到39k的特征点

描述子

设描述子网络为：
$$\text{d}=h_{\rho }({\text{P}}_{\theta })$$
其中，$\text{d}$为计算得到的描述子向量，${\text{P}}_{\theta }$为旋转过后的patch，其中patch的位置和旋转由sift特征点确定。
因此定义损失函数：
$${\mathcal{L}}_{\text{desc }}\left({\mathbf{p}}_{\theta }^k,{\mathbf{p}}_{\theta }^l\right)=\{\begin{array}{l}{\Vert h_{\rho }\left({\mathbf{p}}_{\theta }^k\right)-h_{\rho }\left({\mathbf{p}}_{\theta }^l\right)\Vert }_2\\ \max (0,C\end{array}$$