数据结构与算法（5）排序算法（理论）

1. 排序算法

最常用的排序算法：

冒泡排序、插入排序、选择排序、归并排序、快速排序、计数排序、基数排序、桶排序。

按照时间复杂度可分为三类：

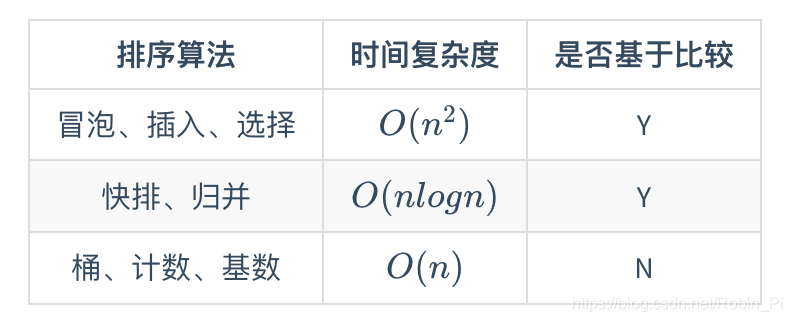
时间复杂度O(n^2)​的三种排序算法

冒泡排序（Bubble Sort）

冒泡排序只会操作相邻的两个数据。每次冒泡操作都会对相邻的两个元素进行比较，看是否满足大小关系要求。如果不满足就让它俩互换。一次冒泡会让至少一个元素移动到它应该在的位置，重复 n 次，就完成了 n 个数据的排序工作。
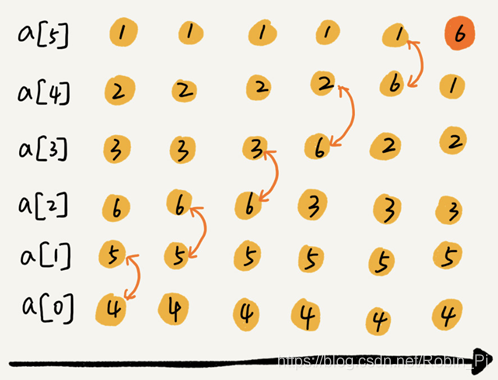经过一次冒泡操作之后，6 这个元素已经存储在正确的位置上。要想完成所有数据的排序，只要进行 6 次这样的冒泡操作就行了：

这个冒泡过程还可以优化。当某次冒泡操作已经没有数据交换时，说明已经达到完全有序，不用再继续执行后续的冒泡操作。

插入排序（Insertion Sort）

插入排序（Insertion Sort）：放在已排序区间比较

将数组中的数据分为两个区间，已排序区间和未排序区间。初始已排序区间只有一个元素，就是数组的第一个元素。取未排序区间中的元素，在已排序区间中找到合适的插入位置将其插入，并保证已排序区间数据一直有序。重复这个过程，直到未排序区间中元素为空，算法结束。
如下图，要排序的数据是 4，5，6，1，3，2，其中左侧为已排序区间，右侧是未排序区间。

选择排序（Selection Sort）

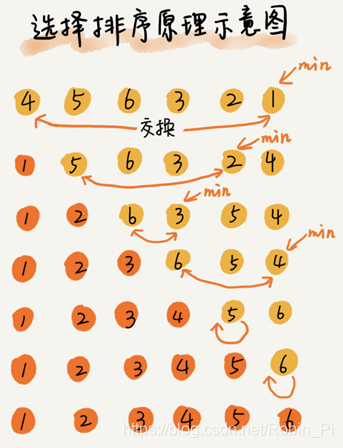
选择排序（Selection Sort）：在未排序区间进行比较

选择排序算法也分已排序区间和未排序区间，每次会从未排序区间中找到最小的元素，将其放到已排序区间的末尾。

希尔排序（Shell Sort）

希尔排序也称递减增量排序算法，是基于插入排序的改进版本。 基本思想是： 先将整个待排序的记录序列分割成为若干子序列分别进行直接插入排序 待整个序列中的记录"基本有序"时,再对全体记录进行依次直接插入排序。

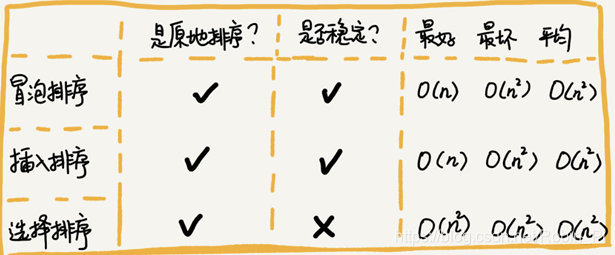
三种 O(n²) 排序算法小结

时间复杂度为 O(nlogn) 的三种排序算法

归并排序和快速排序是时间复杂度为 O(nlogn) 的排序算法，这两种排序算法适合大规模的数据排序，比时间复杂度为 O(n²) 的排序算法要更常用。

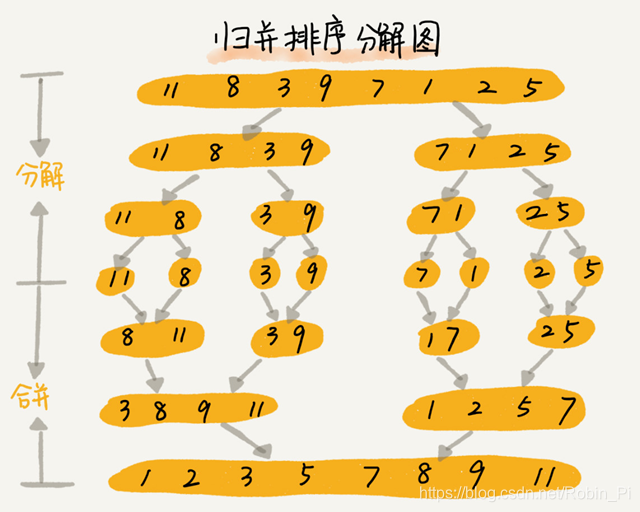
归并排序和快速排序是两种稍微复杂的排序算法，它们用的都是分治的思想，代码都通过递归来实现，过程非常相似。理解归并排序的重点是理解递推公式和 merge() 合并函数。同理，理解快排的重点也是理解递推公式，还有 partition() 分区函数。

归并排序算法是一种在任何情况下时间复杂度都比较稳定的排序算法，这也使它存在致命的缺点，即归并排序不是原地排序算法，空间复杂度比较高，是 O(n)。正因为此，它也没有快排应用广泛。

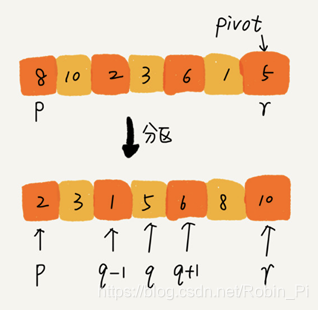
快速排序算法虽然最坏情况下的时间复杂度是 O(n²)，但是平均情况下时间复杂度都是 O(nlogn)。不仅如此，快速排序算法时间复杂度退化到 O(n²) 的概率非常小，可以通过合理地选择 pivot 来避免这种情况。

归并排序（Merge Sort）

快速排序（Quicksort）

2. 排序算法的三个分析指标

2.1 执行效率

排序算法的执行效率，一般从这几个方面来衡量：

（1）最好情况、最坏情况、平均情况时间复杂度
要分别给出最好情况、最坏情况、平均情况下的时间复杂度，并说出最好、最坏时间复杂度对应的要排序的原始数据是什么样的。

• 最好情况
• 最坏情况
• 平均时间复杂度的分析：“有序度”和“逆序度”

有序度是数组中具有有序关系的元素对的个数。表达式：有序元素对：a[i] <= a[j], 如果 i < j。

对于一个倒序排列的数组，有序度是 0；
完全有序的数组的有序度叫作满有序度；

逆序度的定义正好跟有序度相反（默认从小到大为有序）：逆序元素对：a[i] > a[j], 如果 i < j

逆序度 = 满有序度 - 有序度。

排序的过程就是一种增加有序度，减少逆序度的过程，最后达到满有序度，就说明排序完成了。

（2）时间复杂度的系数、常数 、低阶
时间复杂度反应的是数据规模 n 很大的时候的一个增长趋势，它会忽略系数、常数、低阶。

但排序的是 1000 以内规模很小的数据，对同阶时间复杂度的排序算法性能对比的时候，应当把系数、常数、低阶也考虑进来。

（3）比较次数和交换（或移动）次数
基于比较的排序算法的执行过程，会涉及元素比较大小和元素交换或移动两种操作。

在分析排序算法的执行效率的时候，应该把比较次数和交换（或移动）次数也考虑进去。

2.2 内存消耗

算法的内存消耗可以通过空间复杂度来衡量。

原地排序（Sorted in place）算法，是特指空间复杂度是 O(1) 的排序算法。

2.3 稳定性

稳定性是指如果待排序的序列中存在值相等的元素，经过排序之后，相等元素之间原有的先后顺序不变。

比如有一组数据 2，9，3，4，8，3，按照大小排序之后是 2，3，3，4，8，9。

这组数据里有两个 3。经过某种排序算法排序之后，如果两个 3 的前后顺序没有改变，那我们就把这种排序算法叫作稳定的排序算法；如果前后顺序发生变化，那对应的排序算法就叫作不稳定的排序算法。