机器学习模型/算法—— 阶段性总结（2）：关键概念/技术

1. 正则项/惩罚项、过拟合

机器学习的终极目标：期望风险最小

损失函数：期望风险在实际中的定义

风险这个词比较模糊，在实际风险定义中会依赖一个所谓的损失函数

期望风险：分类器真实风险最好的表达

期望风险是全局的，可以看做是真实风险的合理表示。它基于所有样本损失的最小化，期望风险是全局最优，是理想化的不可求的, 从式子可以看出期望风险依赖于数据的联合分布p(x,y)以及损失函数L的定义(依赖于数据y和f(x))

样本无限：

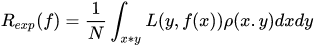
经验风险：期望风险在样本有限情况下的退化

经验风险是局部的，基于训练样本的损失函数最小化，经验风险的优化问题是现实的可求的, 从式子可以看出经验风险仅依赖于数据(x,y)及损失函数L的定义(依赖于数据y和f(x))。

样本有限：

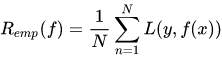
结构风险：期望风险和经验风险的一种平衡

当样本空间很小时，单纯考虑经验风险最小化学习的效果就未必很好，会产生“过拟合(over-fitting)”现象。
主要是因为在样本集个数n小于break point时, 即总能找到一个假设使得分类器将所有训练样本正确分类。换句话说，分类器复杂度高(性能太好)，导致了过拟合。那么既然分类器复杂程度高会导致学习性能下降， 我们就可以把度量分类器复杂程度的一个量（惩罚），加到经验风险损失上。

在经验风险上加上表示模型复杂度的正则项(regularizer)或者罚项(penalty term) 就构成了所谓结构风险。在假设空间F、损失函数以及训练数据集确定的情况下，结构风险的定义为：

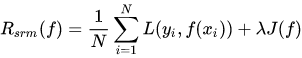
其中，J(f)表示模型的复杂度，λ表示其权重。将分类器复杂度与经验风险一起考虑的优化问题，被定义为结构风险最小化。

如何解决机器中模型泛化能力和过拟合现象的矛盾可以参考 机器学习算法/模型——模型泛化：偏差、方差、噪声

2. 偏置、假设

2.1 偏置的现实来源？

假设函数的偏置 = 误差项 = 噪声 = 偶然性 = 波动

我们最终需要的模型要用来表征实际的情况。但模型不可能百分百正确地反映真实情况，总有误差，因此我们可以给这个模型加上个误差项 $ϵ$（或者说噪音）。例如，

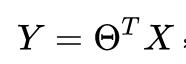
重新写成：

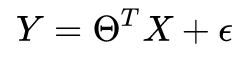
注意：区分偏置和正则项。

---

“归纳偏置” 百度百科：

机器学习试图去建造一个可以学习的算法，用来预测某个目标的结果。要达到此目的，要给于学习算法一些训练样本，样本说明输入与输出之间的预期关系。然后假设学习器在预测中逼近正确的结果，其中包括在训练中未出现的样本。既然未知状况可以是任意的结果，若没有其它额外的假设，这任务就无法解决。 这种关于目标函数的必要假设就称为归纳偏置（Mitchell, 1980; desJardins and Gordon, 1995）。

一个典型的归纳偏置例子是奥卡姆剃刀，它假设 最简单而又一致的假设是最佳的。 这里的一致是指学习器的假设会对所有样本产生正确的结果。

以下是机器学习中常见的归纳偏置列表：

• 最大条件独立性（conditional independence）：如果假说能转成贝叶斯模型架构，则试着使用最大化条件独立性。这是用于朴素贝叶斯分类器（Naive Bayes classifier）的偏置。
• 最小交叉验证误差：当试图在假说中做选择时，挑选那个具有最低交叉验证误差的假说，虽然交叉验证看起来可能无关偏置，但天下没有免费的午餐理论显示交叉验证已是偏置的。
• 最大边界：当要在两个类别间画一道分界线时，试图去最大化边界的宽度。这是用于支持向量机的偏置,它假设不同的类别是由宽界线来区分。
• 最小描述长度（Minimum description length）：当构成一个假设时，试图去最小化其假设的描述长度。假设越简单，越可能为真的。见奥卡姆剃刀。
• 最少特征数（Minimum features）：除非有充分的证据显示一个特征是有效用的，否则它应当被删除。这是特征选择（feature selection）算法背后所使用的假设。
• 最近邻居：假设在特征空间（feature space）中一小区域内大部分的样本是同属一类。给一个未知类别的样本，猜测它与它最紧接的大部分邻居是同属一类。这是用于最近邻居法的偏置。这个假设是相近的样本应倾向同属于一类别。

---

奥卡姆剃刀

“切勿浪费较多东西，去做‘用较少的东西，同样可以做好的事情’‘
我们将对现象的最简单解释称为好的规律。
如无必要勿增实体。
“我们需要承认，自然事物各种现象的真实而有效的原因，除了它自身以外再无须其他，所以，对于同样的自然现象，我们必须尽可能地归于同一原因。”
“如果可能，用已知实体组成的结构，来替换未知实体的推断。”
预测基于一串已知符号的下一个符号会是什么。它唯一的假设就是环境遵从某种未知的但是可计算的概率分布。这个理论是奥卡姆剃刀的数学公理化。

2.2 模型中偏置的意义

没有偏置项 = 分类器模型（决策面）只能经过原点 = 模型无法很好的上下“移动”获得更好的分割效果

3. 线性模型

线性模型本质上是均值预测

线性模型试图学得一个通过属性（特征）的线性组合来进行预测的函数。

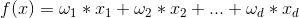
线性模型本质上是均值预测。

线性模型中 f(x) 可以是各种“尺度”上的函数，例如：
f(x)为离散的值：线性多分类模型
f(x)为实数域上实值函数：线性回归模型
f(x)为对数：对数线性模式
f(x)进行sigmoid非线性变换：对数几率回归
…

实际上 ，f(x)可以施加任何形式的变换，需要理解的是，不同的变换之间没有本质的区别，也没有好坏优劣之分，不同的变换带来不同的性质，而不同的性质可以用于不同的场景。

线性模型参数求解的本质 - 线性方程组求解

线性模型蕴含了“原子可叠加性”和“可解释性“的思想

1. 原子可叠加性：许多功能更为强大的非线性模型（nonlinear model）可在线性模型的基础上通过引入层级结构或高维映射而得到；
2. 可解释性（comprehensibility）：权重向量 w 直观表达了各个属性在预测中的重要性（主要矛盾和次要矛盾），而误差偏置 b 则表达了从物理世界到数据表达中存在的不确定性，即数据不能完整映射物理世界中的所有隐状态，一定存在某些噪声无法通过数据表征出来；

---

补：回归分析

相关变量的关系有两种，一种是相关关系，一种是依存关系。

一个变量变化受另一个变量的影响——依存关系，回归分析是研究呈依存关系的相关变量之间的关系

变量之间的关系可分为两类：

1. 存在完全确定的关系——称为函数
2. 关系不存在完全确定的关系——虽然变量间有着十分密切的关系，但是不能由一个或多各变量值精确地求出另一个变量的值，称为相关关系，存在相关关系的变量称为相关变量

相关变量的关系也可分为两种：

1. 两个及以上变量间相互影响——平行关系
2. 一个变量变化受另一个变量的影响——依存关系

它们对应的分析方法：
相关分析是研究呈平行关系的相关变量之间的关系
回归分析是研究呈依存关系的相关变量之间的关系

---

线性回归 - 基于线性模型的一种回归预测模型

线性回归（linear regression）试图学得一个线性模型，以尽可能准确地预测实值输出标记。

对数几率回归 - 基于线性回归的一种概率函数

线性判别分析（ LDA） - 基于线性模型的线性投影判别算法

线性判别分析（linear discriminant analysis LDA）是一种经典的线性学习方法，在二分类问题上最早由Fisher提出，因此亦称为“Fisher判别分析”（Fisher linear discriminant analysis）。

LDA的思想非常朴素：

1. 给定训练样例集，设法将样例投影到一条直线上，使得同类样例的投影点尽可能接近、异类样例的投影点尽可能远离；
2. 在对新样本进行分类时，将其投影到同样的这条直线上，再根据投影点的位置来确定新样本的类别；

下图给出了一个二维示意图：
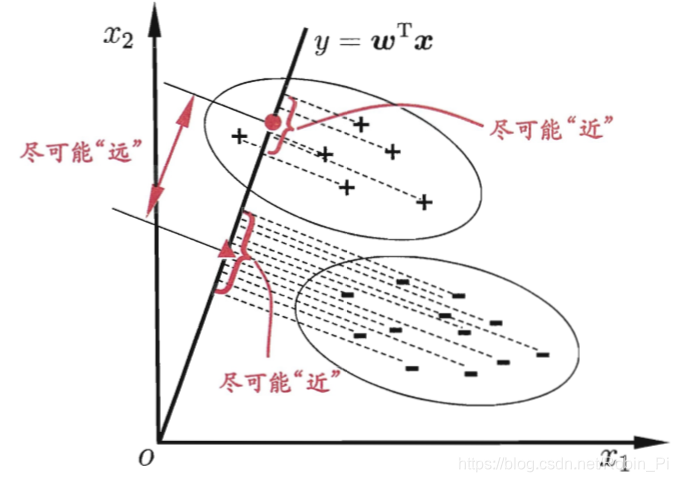- LDA 和 PCA
在machine learning领域，PCA和LDA都可以看成是数据降维的一种方式。但是PCA是unsupervised，而LDA是supervised。

所以PCA和LDA虽然都用到数据降维的思想，但是监督方式不一样，目的也不一样。

PCA是为了去除原始数据集中冗余的维度，让投影子空间的各个维度的方差尽可能大，也就是熵尽可能大；LDA是通过数据降维找到那些具有discriminative的维度，使得原始数据在这些维度上的投影，不同类别尽可能区分开来，而同类别之间尽量相近。

显然，这2种算法内核都借助方差矩阵实现最优化算法，从而实现数据降维压缩的目的。

4. 数据

类别不平衡问题（class-imbalance）

5.距离

机器学习中相似性的度量/距离方法

“距离”真是个好东西。距离于聚类算法的重要性不言而喻，但是仔细想想，机器学习最重要的任务——分类，其本质任务不就是通过距离度量对数据进行划分类别？——距离越近则越相似，越有可能是同类。

机器学习中的相似性度量

损失函数其实就是单个之间差异/距离的度量啊！

损失函数、经验风险、期望风险、结构风险？

目标函数 = 结构风险函数 = 经验风险函数 + 正则项

• 经验风险和期望风险

  经验风险是局部的，基于训练集所有样本点损失函数最小化的。

  期望风险是全局的，是基于所有样本点的损失函数最小化的。

  经验风险函数是现实的，可求的；

  期望风险函数是理想化的，不可求的；

• 结构风险
  只考虑经验风险的话，会出现过拟合的现象，这个时候就引出了结构风险。
  结构风险是对经验风险和期望风险的折中。在经验风险函数后面加一个正则化项（惩罚项）便是结构风险了。

6. 判别模型和生成模型

由生成模型与判别模型引发出的思考

参考

1. 统计学习理论

2. 归纳偏置

3. 线性回归

4. 线性模型

5. 什么是“线性”？

6. 线性回归：描述变量间预测关系最简单的回归模型

7. 简单相关性分析(两个连续型变量)

8. 机器学习–>期望风险、经验风险与结构风险之间的关系

9. 浅谈「正定矩阵」和「半正定矩阵」