矩阵距离和范数+python实现暂记+

向量或矩阵距离相关定义

The Euclidean row distance between rows i and j

$$D_{ij}=\sqrt{\sum _{k=1}^p(X_{ik}-X_{jk}{)}^2}$$
The Euclidean column distance

$$D_{ij}=\sqrt{\sum _{k=1}^n(X_{ki}-X_{kj}{)}^2}$$

The Mahalanobis distance（马氏距离）

$$D_{ij}=\sqrt{(X_i-X_j{)}^{\prime }{S}^{-1}(X_i-X_j)}$$
$S^{-1}为X的协方差矩阵的逆矩阵$
Mahalanobis 距离实际上是加权欧几里得距离，其中权重由协方差矩阵确定。

The Minkowsky row distance （Minkowsky 行距离）

$$D_{ij}=\sum _{k=1}^p(|X_{ik}-X_{jk}{|}^P{)}^{1/P}$$
列距离相似。Minkowsky 距离是行（或列）的对应元素之间的绝对差之和的P次方的P次方根。欧几里得距离是P = 2 的特例。

The block row distance （块行距离）

$$D_{ij}=\sum _{k=1}^p|X_{ik}-X_{jk}|$$

列距离相似，但总和是行数而不是列数。块距离是行（或列）的对应元素之间的绝对差之和。请注意，这是P = 1 的 Minkowsky 距离的特殊情况，曼哈顿距离。
.1-范数（曼哈顿距离Manhattan distance）

The Chebychev row distance （Chebychev 行距离）

$$D_{ij}=\underset{k}{\max }|X_{ik}-X_{jk}|$$
列距离相似。

$$D_{CosineSimilarity}=\frac{{\sum }_{k=1}^n{x}_{ik}{y}_{jk}}{\sqrt{{\sum }_{k=1}^n{x}_{ik}^2}\sqrt{{\sum }_{k=1}^n{y}_{jk}^2}}$$

The cosine distance

$$D_{CosineDistance}=1-D_{CosineSimilarity}$$
上面的余弦距离仅针对正值定义。施瓦茨不等式不成立也不是适当的距离。但是，以下角度定义是正确的距离：

$$D_{angularcosinedistance}=\frac{c\cdot \arccos (D_{cosinesimilarity})}{\pi }$$
如果没有负值，则c = 2，如果有负值，则 c = 1。

$$D_{angularcosinesimilarty}=1-D_{angularcosinedistance}$$

如果在输入中遇到负值，则不会计算余弦距离。但是，将计算余弦相似度。
列距离和相似度的定义类似，但总和是在行而不是列上。

The Canberra row distance (堪培拉行距离)

$$D_{ij}=\sum _{k=1}^p\frac{|X_{ik}-Y_{jk}|}{|X_{ik}|+|Y_{jk}|}$$
列距离相似，但总和是在行而不是列上。

堪培拉距离是街区（曼哈顿）距离的加权版本。

The Jaccard row similarity (Jaccard 行相似度)

$$S_{ij}=\frac{{\sum }_{k=1}^p\min (X_{ik},Y_{jk})}{{\sum }_{k=1}^p\max (X_{ik},Y_{jk})}$$

Jaccard row distance

$$D_{ij}=1-S_{ij}$$

The Pearson row distance

$$D_{ij}=(1-R_{ij})/2$$
$R_{ij}是行i和j之间的相关系数$

The Pearson row similarity

$$S_{ij}=1-D_{ij}$$

The Hamming row distance

$$D_{ij}=在第i行和第j行之间不同的元素数$$

向量或矩阵范数

	向量	矩阵
0 范数	非零元素的个数	没找到相关定义(不过可由向量范数诱导矩阵范数,可能严格地从范数的公理来说得不到0范数)
1-范数	元素绝对值之和	矩阵列向量绝对值之和的最大值
Frobenius范数		矩阵元素绝对值的平方之和的开方
2-范数		$\sqrt{A^{T}A的最大特征值}$
p-q范数		$||A|{|}_{p,q}=({\sum }_{j=1}^n({\sum }_{i=1}^m|a_{i,j}{|}^p){)}^{\frac{1}{q}}$
核范数		奇异值之和

矩阵距离代码实现

一些常用的范数

torch.norm

p	例子
nuclear norm	奇异值的和
p-范数	torch.norm(c, p=1, dim=1) 或 torch.norm(a, float(‘inf’))
Frobenius norm，2-范数	def norm(input, p=“fro”, dim=None, keepdim=False, out=None, dtype=None)

其他参数
keepdim	whether the output tensors have dim retained or not
dim	定要计算范数的一个或多个维度dim。如果dim是空，则范数将在 的所有维数上计算

torch.linalg.norm

torch.linalg.norm(A, ord=None, dim=None, keepdim=False, *, out=None, dtype=None) 

ord	解释	例子
		from torch import linalg as LA
无 或 fro	2-范数	LA.norm(a)
nuc	核范数
inf	max(sum(abs(x), dim=1))	LA.norm(a, float(‘inf’))
-inf	min(sum(abs(x), dim=1))	LA.norm(B, -float(‘inf’))
1	max(sum(abs(x), dim=0))	LA.norm(B, 1)
-1	min(sum(abs(x), dim=0))	LA.norm(B, -1)
2	最大奇异值	LA.norm(B, 2)
-2	最小奇异值	LA.norm(B.double(), -2)

汉明距离

向量汉明距离

# https://zhuanlan.zhihu.com/p/366064507   https://leetcode.cn/problems/hamming-distance/
def hammingDistance(x, y):
    xor = x ^ y
    distance = 0
    while xor:
        distance = distance + 1
        xor = xor & (xor - 1)
    return distance

余弦距离

向量余弦距离torch.nn.CosineSimilarity(这个是对应向量的)

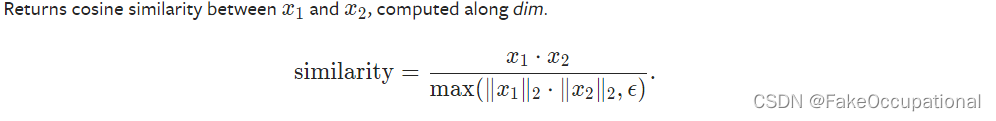
# Import the required library
import torch

# define two input tensors
tensor1 = torch.tensor([0.1, 0.3, 2.3, 0.45])
tensor2 = torch.tensor([0.13, 0.23, 2.33, 0.45])

# print above defined two tensors
print("Tensor 1:\n", tensor1)
print("Tensor 2:\n", tensor2)

# define a method to measure cosine similarity
cos = torch.nn.CosineSimilarity(dim=0)
output = cos(tensor1, tensor2)

# display the output tensor
print("Cosine Similarity:",output)

Tensor 1:
   tensor([0.1000, 0.3000, 2.3000, 0.4500])
Tensor 2:
   tensor([0.1300, 0.2300, 2.3300, 0.4500])
Cosine Similarity: tensor(0.9995)

# Import the required library
import torch

# define two input tensors
tensor1 = torch.randn(3,4)
tensor2 = torch.randn(3,4)

# print above defined two tensors
print("Tensor 1:\n", tensor1)
print("Tensor 2:\n", tensor2)

# define a method to measure cosine similarity in dim 0
cos0 = torch.nn.CosineSimilarity(dim=0)
output0 = cos0(tensor1, tensor2)
print("Cosine Similarity in dim 0:\n",output0)

# define a method to measure cosine similarity in dim 1
cos1 = torch.nn.CosineSimilarity(dim=1)
output1 = cos1(tensor1, tensor2)
print("Cosine Similarity in dim 1:\n",output1)

Tensor 1:
   tensor([[ 0.2714, 1.1430, 1.3997, 0.8788],
      [-2.2268, 1.9799, 1.5682, 0.5850],
      [ 1.2289, 0.5043, -0.1625, 1.1403]])
Tensor 2:
   tensor([[-0.3299, 0.6360, -0.2014, 0.5989],
      [-0.6679, 0.0793, -2.5842, -1.5123],
      [ 1.1110, -0.1212, 0.0324, 1.1277]])
Cosine Similarity in dim 0:
   tensor([ 0.8076, 0.5388, -0.7941, 0.3016])
Cosine Similarity in dim 1:
   tensor([ 0.4553, -0.3140, 0.9258])

https://www.tutorialspoint.com/how-to-compute-the-cosine-similarity-between-two-tensors-in-pytorch

矩阵余弦距离pytorch

a = torch.tensor([1,2])
b = torch.tensor([2,3])
norm_of_a = torch.norm(a)
norm_of_b = torch.norm(b)
cos_dis = 1 -( torch.sum(a*b)/(norm_of_a*norm_of_b))

Pearson相关系数

$$R_{ij}=\frac{C_{ij}}{\sqrt{C_{ii}\ast C_{jj}}}$$

numpy实现

# 官方链接还有矩阵的实现例子代码 https://numpy.org/doc/stable/reference/generated/numpy.corrcoef.html
import numpy as np
x = np.array([0.77395605, 0.43887844, 0.85859792])
y = np.array([0.69736803, 0.09417735, 0.97562235])
res = np.corrcoef(x, y)
print(res)

或、

import numpy as np
x = np.array([[0.77395605, 0.43887844, 0.85859792],[0.69736803, 0.09417735, 0.97562235]])
res = np.corrcoef(x)
print(res)

## 输出 1处对角线为自相关系数 其他位置(如res[0,1])为互相关系数
[[1.         0.99256089]
 [0.99256089 1.        ]]

scipy 实现

#使用Python scipy  https://zhuanlan.zhihu.com/p/411907389+
from scipy import stats

a = np.array([0, 0, 0, 1, 1, 1, 1])
b = np.arange(7)
c,p = stats.pearsonr(a, b)
print('Pearson correlation：%s'%c)
print('p-value：%s'%p)

参考与更多

torch.linalg.norm
torch.norm
文本相似度的BERT度量方法
From Word Embeddings To Document Distance 小结
为什么核范数能凸近似矩阵的秩？为什么核范数是凸的？