每周五篇博客:(3/5)
https://codeforces.com/contest/2106
F. Goblin
TC博士有一个名为Goblin的新患者。他想测试地精的智能,但他对自己的标准测试感到无聊。因此,他决定使它变得更加困难。
首先,他创建一个具有 nnn 字符的二进制字符串 ∗^{\text{∗}}∗ sss 。然后,他创建 nnn 二进制字符串 a1,a2,…,ana_1, a_2, \ldots, a_na1,a2,…,an 。众所周知, aia_iai 是通过首先复制 sss 而创建的,然后翻转 iii \ - Th targue( 1\texttt{1}1 )变成 0\texttt{0}0 和VICE VERSA)。创建所有 nnn 字符串后,他将它们安排到 n×nn \times nn×n 网格中,其中 gi,j=aijg_{i, j} = a_{i_j}gi,j=aij 。
一个大小的 SSS kkk 包含不同整数对 {(x1,y1),(x2,y2),…,(xk,yk)}\{(x_1, y_1), (x_2, y_2), \ldots, (x_k, y_k)\}{(x1,y1),(x2,y2),…,(xk,yk)} 的集合被认为是不错的。
- 1≤xi,yi≤n1 \leq x_i, y_i \leq n1≤xi,yi≤n ,用于所有 1≤i≤k1 \leq i \leq k1≤i≤k 。
- 所有 1≤i≤k1 \leq i \leq k1≤i≤k 的 gxi,yi=0g_{x_i, y_i} = \texttt{0}gxi,yi=0 。
- 对于任何两个整数 iii 和 jjj ({ 1≤i,j≤k1 \leq i, j \leq k1≤i,j≤k ),可从坐标 (xj,yj)(x_j, y_j)(xj,yj) 坐标 (xi,yi)(x_i, y_i)(xi,yi) ,通过通过相邻单元格(共享一个侧面)的序列( (xj,yj)(x_j, y_j)(xj,yj) ),这些 (xj,yj)(x_j, y_j)(xj,yj) 拥有一个有价值的{399999999999999。
哥布林的任务是找到良好集 SSS 的最大可能大小。因为TC博士很慷慨,这次他给了他两秒钟的时间来找到答案,而不是一个。哥布林以诚实而闻名,因此他要求您帮助他作弊。
∗^{\text{∗}}∗ 二进制字符串是一个仅由字符组成的字符串 1\texttt{1}1 和 0\texttt{0}0 。
思路
打表推公式题
分成三种情况:
- 00…0000\dots0000…00 ,首先令这一段零的左右端点分别为 l,rl, rl,r 。这一段的贡献为 (r−l+1)×(r−l+1−1)2+(r−l+1)×max(l−1,n−r)\frac {(r - l + 1)\times (r - l + 1 - 1)} {2} + (r - l + 1) \times \max(l - 1, n - r)2(r−l+1)×(r−l+1−1)+(r−l+1)×max(l−1,n−r) 。此外要计算 l−1l-1l−1 和 n−rn - rn−r 直接的关系,如果 l−1>n−rl - 1 > n - rl−1>n−r 的话那么应该判断 lll 是否等于 111 ,不等于的话应该 +1+1+1。l−1<n−rl - 1 < n- rl−1<n−r 的话应该判断 rrr 是否等于 nnn。
原理是判断 000 选择构造的矩阵的上/下半部分。这里的矩阵上/下部分是指,例如 000000000 会构造出
1 0 0
0 1 0
0 0 1
右上角构造的 000 称为上半部分,左下角的部分称为下半部分
- 00…00100…0000\dots00 1 00\dots0000…00100…00 ,这种情况因为当 111 改变时会将两段 000 给连接起来,所以贡献应该特殊考虑。令两段零的左右端点分别为 l1,r1,l2,r2l1, r1, l2, r2l1,r1,l2,r2 。贡献为 $(r1 - l1 + 1) \times (n - r1) + \frac {(r1 - l1 + 1)(r1 - l1 + 1 - 1)}{2} + 1 + (r2 - l2 + 1) \times (l2 - 1) + \frac {(r2 - l2 + 1)(r2 - l2 + 1 - 1)}{2} $ 。
例如 001000010000100 可以构造
1 0 1 0 0
0 1 1 0 0
0 0 0 0 0
0 0 1 1 0
0 0 1 0 1
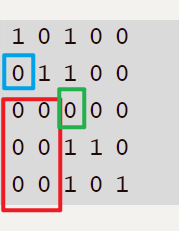
红框部分的计算是 (r1−l1+1)×(n−r1)(r1 - l1 + 1) \times (n - r1)(r1−l1+1)×(n−r1) 。蓝框部分是 (r1−l1+1)(r1−l1+1−1)2\frac {(r1 - l1 + 1)(r1 - l1 + 1 - 1)}{2}2(r1−l1+1)(r1−l1+1−1) ,绿框是 $ + 1$
- 00…001…100…0000\dots001\dots100\dots0000…001…100…00 ,这一部分中因为中间有多个 111 ,所以两段 000 不可能连接在一起要分开计算,所以参考情况 111
代码
void solve() {
i64 n;
std::cin >> n;
std::string s;
std::cin >> s;
s = "?" + s;
std::vector<PII> a;
for (int l = 1, r; l <= n; l = r + 1) {
r = l;
if (s[l] == '1') continue;
while (r + 1 <= n && s[r + 1] == '0') r ++;
a.emplace_back(l, r);
}
if (a.empty()) {
std::cout << "1\n";
return ;
}
auto get = [&](i64 l, i64 r) ->i64 {
i64 len = r - l + 1;
i64 ans = (len * (len - 1)) / 2 + (r - l + 1) * std::max(n - r, l - 1);
if (n - r == l - 1) ans += (l != 1 || r != n);
else if (n - r > l - 1) ans += (r != n);
else ans += (l != 1);
return ans;
};
auto calc = [&](i64 l1, i64 r1, i64 l2, i64 r2) ->i64 {
i64 len1 = r1 - l1 + 1;
i64 len2 = r2 - l2 + 1;
return len1 * (n - r1) + (len1 - 1) * len1 / 2 + 1 + len2 * (l2 - 1) + (len2 - 1) * len2 / 2;
};
i64 ans = get(a[0].first, a[0].second);
for (int i = 1; i < a.size(); i ++) {
auto [l1, r1] = a[i - 1];
auto [l2, r2] = a[i];
ans = std::max(ans, get(l2, r2));
if (r1 == l2 - 2) ans = std::max(ans, calc(l1, r1, l2, r2));
}
std::cout << ans << '\n';
}
G1. Baudelaire (easy version)
这是问题的简单版本。两个版本之间的唯一区别是,在此版本中,可以确保每个节点都与节点相邻 111 。
这个问题是互动的。
鲍德莱尔(Baudelaire)非常富裕,因此他购买了一棵大小 nnn 的树,该树植根于某个任意节点。此外,每个节点的值为 111 或 −1-1−1 。在此版本中,每个节点都与节点 111 相邻。但是,请注意,节点 111 不一定是根。
牛书呆子看到了树,爱上了它。但是,计算机科学不足以支付他的费用,因此他负担不起购买。鲍德莱尔(Baudelaire)决定与书呆子的牛玩游戏,如果他赢了,他会给他送给他这棵树。
牛书呆子不知道哪个节点是根,他也不知道节点的值。但是,他可以询问两种类型的Baudelaire查询:
- 111 kkk u1u_1u1 u2u_2u2 ......... uku_kuk : Let f(u)f(u)f(u) be the sum of the values of all nodes in the path from the root of the tree to node uuu 。牛书呆子可以选择一个整数 kkk (1≤k≤n)(1 \le k \le n)(1≤k≤n) 和 kkk nodes {488885079},他将获得值 f(u1)+f(u2)+...+f(uk)f(u_1) + f(u_2) + ... + f(u_k)f(u1)+f(u2)+...+f(uk) 。
- 222 uuu :Baudelaire将切换节点 uuu 的值。具体而言,如果 uuu 的值为 111 ,它将变为{233777312},反之亦然。
牛书呆子在 n+200n + 200n+200 内正确地猜出每个节点的值(最终树的值,在执行查询之后的值之后的值)。你能帮他赢吗?
思路
考虑前缀和,定义 sumisum_isumi 为根到节点 iii 的权值和 ,令 faifa_ifai 为 iii 的父亲节点,令 aia_iai 为节点 iii 的权值。则有 ai=sumi−sumfaia_i = sum_i - sum_{fa_i}ai=sumi−sumfai。首先利用 nnn 次查询得到 sumisum_isumi
此外,如果一个节点 uuu 的值进行了修改,那么其子树所有的 sumisum_isumi 都会被修改为 sumi’sum_i ’sumi’。并且有 ∣sumi−sumi′∣=2|sum_i - sum_i'| = 2∣sumi−sumi′∣=2。而其父亲节点的值是不会发生改变的
在本题树是一个菊花树,所以分成两种情况:
- 节点 111 是根
- 节点 111 不是根
首先假设节点 111 是根,那么我们先反转 111 的值,然后查询 ∑i=2nsumi′\sum_{i = 2}^n sum_i'∑i=2nsumi′,因为之前通过 nnn 次查询已经知道了 sumisum_isumi ,所以可以先预处理出 ∑i=2nsumi\sum_{i = 2} ^n sum_i∑i=2nsumi ,然后判断 ∣∑i=2nsumi−∑i=2nsumi′∣|\sum_{i = 2} ^n sum_i - \sum_{i = 2}^n sum_i'|∣∑i=2nsumi−∑i=2nsumi′∣ 是否等于 2×(n−1)2 \times (n - 1)2×(n−1) 。如果等于的话,就说明 [2,n][2, n][2,n] 区间没有节点是 111 的父亲,那么 111 显然就是根节点了,对于其他节点的权值有 ai=sumi−sum1a_i = sum_i - sum_1ai=sumi−sum1 ,计算后输出即可。如果不等于的话,转换到情况 222
这个时候考虑找到 111 的父亲节点。如果我们修改 111 后查询区间 [l,r][l, r][l,r] ,如果 ∣∑i=lrsumi−∑i=lrsumi′∣=2×(r−l+1)|\sum_{i = l} ^r sum_i - \sum_{i = l}^r sum_i'| = 2 \times(r - l + 1)∣∑i=lrsumi−∑i=lrsumi′∣=2×(r−l+1) 说明区间 [l,r][l, r][l,r] 的节点都在 111 的子树中,那么也就说明区间 [l,r][l, r][l,r] 中不包含 111 的父亲。根据以上信息可以用二分的方式去找到父亲节点,直到 ∣∑i=lrsumi−∑i=lrsumi′∣=0|\sum_{i = l} ^r sum_i - \sum_{i = l}^r sum_i'| = 0∣∑i=lrsumi−∑i=lrsumi′∣=0 就说明找到了父亲节点(此时 l=rl = rl=r。那么对于其他节点的权值有 ai=sumi−sum1a_i = sum_i - sum_1ai=sumi−sum1,对于节点 111 有 a1=sum1−sumra_1 = sum_1 - sum_ra1=sum1−sumr。最后输出即可
代码
void solve() {
int n;
std::cin >> n;
std::vector go(n + 1, std::vector<int>());
for (int i = 1; i < n; i ++) {
int u, v;
std::cin >> u >> v;
go[u].push_back(v);
go[v].push_back(u);
}
std::vector<int> sum(n + 1), a(n + 1);
int s1 = 0;
for (int i = 1; i <= n; i ++) {
std::cout << "? 1 1 " << i << std::endl;
std::cin >> sum[i];
s1 += sum[i];
}
std::cout << "? 2 1" << std::endl;
std::cout << "? 1 " << n - 1 << " ";
for (int i = 2; i <= n; i ++) std::cout << i << " ";
std::cout << std::endl;
int s2;
std::cin >> s2;
s1 -= sum[1];
if (std::abs(s1 - s2) == 2 * (n - 1) && sum[1] != 0) {
a[1] = sum[1];
for (int i = 2; i <= n; i ++) a[i] = sum[i] - sum[1];
std::cout << "? 2 1" << std::endl;
std::cout << "! ";
for (int i = 1; i <= n; i ++) std::cout << a[i] << " ";
std::cout << std::endl;
return ;
}
int l = 2, r = n;
int ok = 1;
while (l < r) {
int mid = l + r >> 1;
int x1, x2;
std::cout << "? 1 " << mid - l + 1 << " ";
for (int i = l; i <= mid; i ++) std::cout << i << " ";
std::cout << std::endl;
std::cin >> x1;
std::cout << "? 2 1" << std::endl;
ok ^= 1;
std::cout << "? 1 " << mid - l + 1 << " ";
for (int i = l; i <= mid; i ++) std::cout << i << " ";
std::cout << std::endl;
std::cin >> x2;
if (std::abs(x1 - x2) == (mid - l + 1) * 2) l = mid + 1;
else r = mid;
}
if (ok) std::cout << "? 2 1" << std::endl;
a[r] = sum[r];
a[1] = sum[1] - sum[r];
for (int i = 2; i <= n; i ++) if (i != r) a[i] = sum[i] - sum[1];
std::cout << "! ";
for (int i = 1; i <= n; i ++) std::cout << a[i] << " ";
std::cout << std::endl;
}





















 1171
1171

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








