在神经网络收敛的计算中,我们一直在使用梯度下降法,但除了梯度下降法,还有很多更加优秀的算法,可以适应更多种情况,从而避免过拟合,未收敛等问题。
动量梯度下降法
具体公式如下。
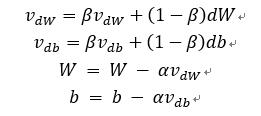
与梯度下降法不一样的是学习率α不再是乘于dW(cost函数对权重W的偏导数),而是变成βv_dW+(1-β)dW。这样计算出来的v_dW不再只依赖于当前的dW,而是跟之前迭代结果的v_dW也有关系,通过变量β来调整过去与现在权重占比。
为了更好的了解这个公式,我们再来看看指数加权平均公式。
指数加权平均数,顾名思义是求平均数,但是不是单纯的把所有的数字加起来再除以数量,而是把过去与现在相关联,乘以各自对应权重而求出平均数。
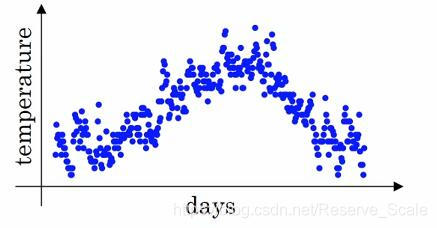
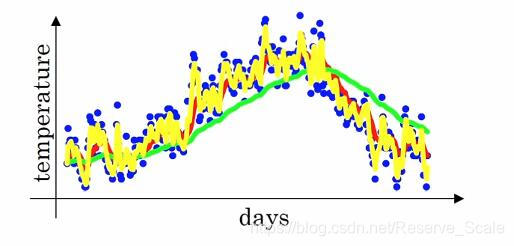
上图横坐标为日期,纵坐标为温度,每个点代表着某一天的温度。
我们把每一天的温度用θ_t表示,当天的平均温度用V_t表示,引入指数加权公式。
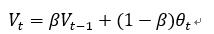
所以在求第n天的平均温度时,不仅要考虑当天的温度θ_t,还要加上V_t-1天的平均温度,也就是n-1天前的平均温度。
了解整个公式的含义后,我们再来看不同的β值对平均数的影响。
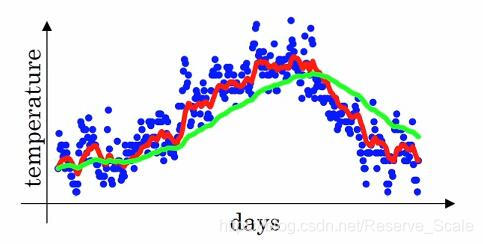
红色的曲线为β=0.9,绿色的曲线为β取值0.98。绿色的曲线相对于红色的曲线会更加的平坦。这是因为根据公式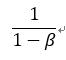 的粗略计算,当β为0.9时,相当于平均了10天的温度,而β等于0.98时,相当于平均了50天的温度,所以绿色的曲线会更加的平缓。但是由于我们我们分配给当前温度的权重只有0.02,导致整个曲线的右移。当我们在取β为0.5时,相当于我们只平均了2天的温度,下图的黄线为结果,曲线变得更加的陡峭。
的粗略计算,当β为0.9时,相当于平均了10天的温度,而β等于0.98时,相当于平均了50天的温度,所以绿色的曲线会更加的平缓。但是由于我们我们分配给当前温度的权重只有0.02,导致整个曲线的右移。当我们在取β为0.5时,相当于我们只平均了2天的温度,下图的黄线为结果,曲线变得更加的陡峭。
这里还存在一个偏差修正的问题,因为我们刚开始计算的时候,并没有V_0的温度,所以我们初始化V_0的温度为0,则会导致(1-β)θ_1的数值很小,即V_1的温度很小,这个结果会影响前几次的迭代,不过在神经网络大量的迭代训练中,基本上可以忽略,所以在神经网络的应用中,很少会使用到偏差修正。
但在这里还是提一下偏差修正的公式如下。
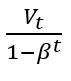 ,以上面的平均温度问题为例,假设β为0.98,t代表当天的天数,则第一天的时候,t等于1,所以V_t除以的分母为50,所以虽然V_0为0,导致V_1经过指数加权后的数值很小,但是乘以50,则会更接近真实的θ_1的温度。
,以上面的平均温度问题为例,假设β为0.98,t代表当天的天数,则第一天的时候,t等于1,所以V_t除以的分母为50,所以虽然V_0为0,导致V_1经过指数加权后的数值很小,但是乘以50,则会更接近真实的θ_1的温度。
我们再回到动量梯度下降法。

这里蓝线为梯度下降法所收敛的过程,我们假设横轴为权重W,纵轴为b,我们希望的是收敛路径往横轴方向上移动的更多,而在纵轴方向最后小范围波动。所以使用动量梯度下降法将会考虑都过去的状态,与现在的状态互相平衡,导致在横轴上的W移动的更快,而b移动的范围更小,如红线所示。

RMSprop算法
具体公式如下。
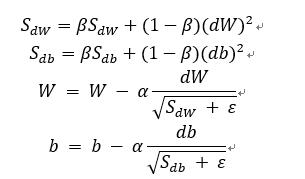
跟动量梯度下降法的目标是一样的,让纵轴摆动更小,横轴加快学习。
ε是一个很小的实数,避免分母为0,一般10的-8次方。
Adam算法
Adam算法结合了动量梯度算法与RMSprop算法,在神经网络优化算法中成为主流优化函数。
具体公式如下。
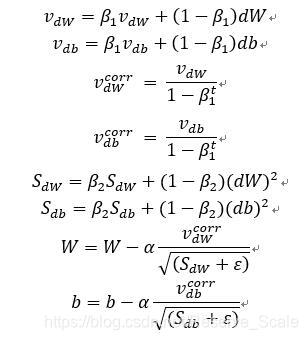
这里我们使用了偏差修正,使结果更加精确。
这里有很多超参数的选择,如α,β1,β2,ε。
β1一般取值为0.9,β2一般取值为0.999,可以在神经网络里尝试各种不一样的超参数的值,选出最合适的那种。
学习率衰减
除了可以选择绣优化函数来进一步提高神经网络的准确率以外,还可以通过学习率衰减来更快的进行函数收敛。
第一种方法:
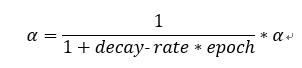
decay-rate为衰减因子,epoch为迭代周期的次数。
第二种方法:
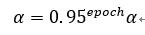




 本文探讨了梯度下降法的多种改进版本,包括动量梯度下降法、RMSprop算法和Adam算法,这些方法通过调整学习率和利用历史梯度信息,有效提升了神经网络的收敛速度和稳定性。
本文探讨了梯度下降法的多种改进版本,包括动量梯度下降法、RMSprop算法和Adam算法,这些方法通过调整学习率和利用历史梯度信息,有效提升了神经网络的收敛速度和稳定性。
















 1509
1509

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








