Datawhale X 李宏毅苹果书 AI夏令营 深度学习入门Task1

Datawhale 2024年AI夏令营的第五期学习活动聚焦于深度学习，第一阶段主要内容是通过案例了解机器学习。

本篇笔记为第一阶段的笔记

本阶段的主要学习任务为初步学习了解机器学习。

一、机器学习的概念及其常见任务

广义的机器学习是指机器具备有学习的能力，即就是让机器具备找一个函数的能力。对于机器学习，常见的任务有回归(regression)和分类(classification)。回归主要是输出数值和标量，在苹果书中，给出的例子是根据前日的PM2.5推出当日的PM2.5的数值。分类将选项分为类别1、类别2等等，例如判断邮件是否为垃圾邮件。除了回归跟分类以外，还有结构化学习(structured learning)。

二、跟随案例深入了解

苹果书中，以视频的点击次数预测为例，将机器学习找函数的过程，分成了3个步骤来阐述。

Step1：写出一个带有未知参数的函数f，能预测未来观看次数。

其中w跟b是未知的参数。w为权重(weight)，b称为偏置(bias)。它们作为未知的参数，往往来自于对这个问题本质上的了解，需要领域知识(domain knowledge)的支撑。

Step2：定义损失(loss)

通过比较模型预测值与实际值之间的差异，我们可以评估模型参数的优劣，并据此调整参数以最小化损失函数，从而改进模型的预测性能。

在机器学习建模中，通过计算平均绝对误差（MAE）和均方误差（MSE）等损失函数，可以评估模型预测性能。使用真实数据测试不同参数组合（w, b），并绘制等高线图直观展示损失大小。红色区域损失大，蓝色区域损失小。找到蓝色区域最低点即最优参数组合，能显著提高预测精准度。对于观看次数预测，w接近1且b较小通常较符合预期，模型预测更精准。

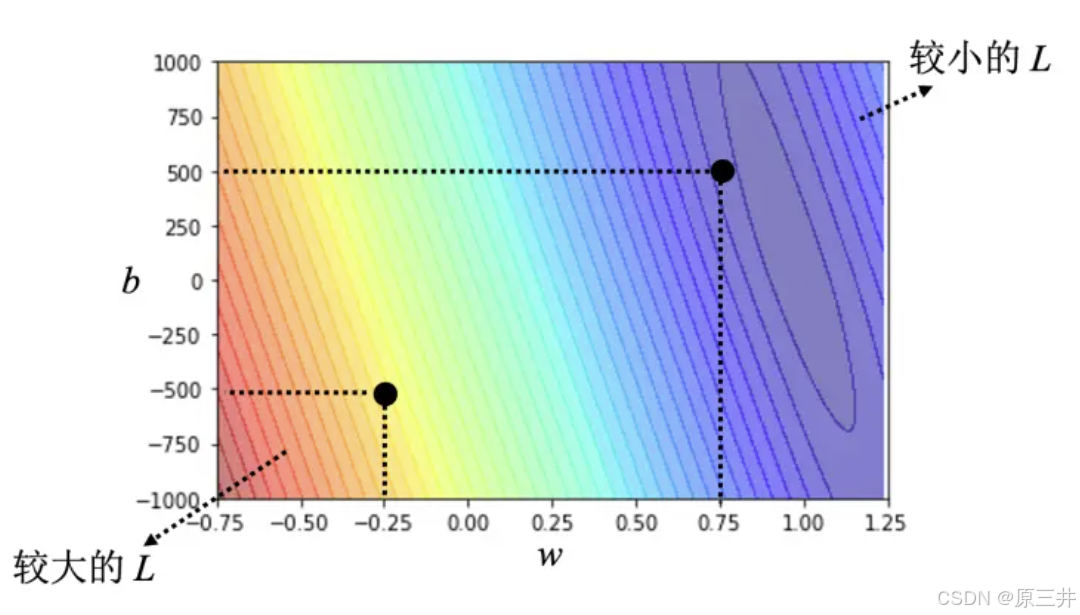
图1 误差表面 

Step3：解最优化的问题

通过梯度下降法寻找最优参数w∗和b∗，以最小化损失函数L。对于单个参数w，从随机初始点开始，计算损失对w的偏导数（斜率），根据斜率正负调整w值以减小损失。步伐大小受斜率和学习率η（超参数）影响。学习率大则步伐大，学习快；学习率小则步伐小，学习慢。通过迭代调整，逐步逼近最优解，使损失最小。

更新次数或微分值为0时停止。但可能陷入局部最小值而非全局最小值。在双参数情况下，同时更新w和b，利用深度学习框架自动计算微分。通过不断迭代，最终找到一组较优的w和b，使得损失函数值较小。实际计算中，w=0.97, b=100，与预期相符，平均误差约480，即预测误差约500人。梯度下降法虽可能面临局部最小值问题，但在实践中常能找到较好的解。

以上为本次Task1学习内容的笔记。感谢Datawhale提供丰富的学习资源。