【C++练习】利用泰勒级数近似计算正弦函数平方和

最新推荐文章于 2026-01-08 22:28:34 发布

原创最新推荐文章于 2026-01-08 22:28:34 发布 · 860 阅读

3 ·

CC 4.0 BY-SA版权

文章标签：

#算法

题目：

利用泰勒级数近似计算正弦函数平方和

问题描述：

编写一个程序，利用泰勒级数（Taylor series）近似计算给定角度（弧度制）的正弦函数值，并进一步计算两个角度正弦值的平方和。泰勒级数展开式是数学中一种重要的无穷级数，可以用来近似许多常见函数，包括正弦函数。

程序要求：

定义一个函数 sin_approx(double x)，该函数使用泰勒级数展开式近似计算并返回角度 x 的正弦值。在近似计算中，当新增项的绝对值小于 10−10 时停止累加。
在 main 函数中，提示用户输入两个浮点数 r 和 s，分别代表两个角度（弧度制）。
使用 sin_approx 函数计算角度 r 和 s 的正弦值，并计算它们的平方和。
输出结果，保留十位小数，格式为：k = sin^2(r) + sin^2(s) ≈ 结果。

源代码：

#include <iostream>  
#include <cmath>  
#include <iomanip>  
using namespace std;

double sin_approx(double x) {
    double sum = 0.0;
    double term = x;
    int n = 1;

    while (fabs(term) > 1e-10) {
        sum += term;
        term *= (-1) * x * x / ((2 * n - 1) * (2 * n));
        n++;
    }

    return sum;
}

int main() {
    double r, s;
    cout << "请输入r的值: ";
    cin >> r;
    cout << "请输入s的值: ";
    cin >> s;

    double result = sin_approx(r) * sin_approx(r) + sin_approx(s) * sin_approx(s);
    cout << fixed << setprecision(10);
    cout << "k = sin^2(" << r << ") + sin^2(" << s << ") ≈ " << result << endl;

    return 0;
}

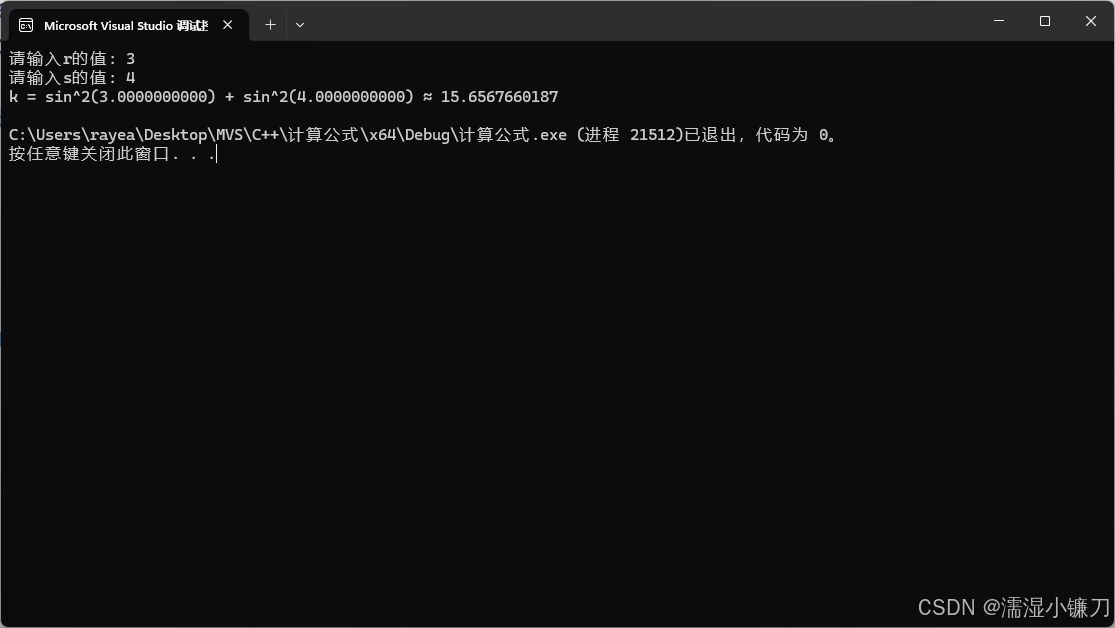
运行截图：