BFS和强连通分量寻找

最新推荐文章于 2021-04-20 00:25:55 发布

原创

最新推荐文章于 2021-04-20 00:25:55 发布 · 862 阅读

1 ·

CC 4.0 BY-SA版权

本文介绍了BFS（广度优先搜索）与DFS（深度优先搜索）的区别，并讨论了如何使用DFS找寻有向图的强连通分量（SCC）。在有向图中，如果两个顶点相互可达，则称它们强连通。通过拓扑排序和边的反向，可以有效地找出图中的强连通分量。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

广度优先走索（BFS）与DFS的区别还是比较明显的：后者是首先朝着一个方向始终探索，直到“死路”才回溯去探索别的路口；后者则是稳步推进的方式，有点类似水纹扩散，一步一步向外扩散。在代码思想上，主要一个是运用FIFO队列一个是FILO队列。大致实现如下：

from collections import deque

def bfs(G, s, seq, ans):	# G是图，s是起始点，seq是FILO队列，ans是探索的所有点的列表
	if seq is None:
		seq == deque()
	seq.append(s)
	ans.append(s)
	while seq:
		s = seq.popleft()
		for u in G[s]:
			if u in seq: continue
			seq.append(u)
			ans.append(s)

学习了DFS和BFS后，对于遍历有了一定的认识，可以使用DFS来找强连通分量（SCC）。有向图强连通分量：在有向图G中，如果两个顶点vi,vj间（vi>vj）有一条从vi到vj的有向路径，同时还有一条从vj到vi的有向路径，则称两个顶点强连通(strongly connected)。如果有向图G的每两个顶点都强连通，称G是一个强连通图。有向图的极大强连通子图，称为强连通分量(strongly connected components)。（取自百度百科）
如果我们对一个有向图进行拓扑排序，就会得到一个这个图的扫描节点结束时间为准的列表之类的答案。一个节点扫描结束时间晚于另一个节点，就意味着前一个点可以到达后一个点，或者两者之间没有通路，是两个强连通分量。如果把图中所有的边的方向反向，强连通分量依然保持，但是两个连通分量之间的前一个节点到达不了后裔连通分量了。
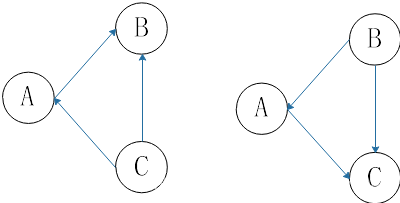
在这里插入图片描述
右图中，如果我们依然从C点搜索，就这能搜索到C点，这也就是第一个强连通分量；然后是A再是B。这样图中的强连通分量就搜索