C++ 一维前缀和
-
- 什么是前缀和
-
- 前缀和算法有什么好处?
1、前缀和
前缀和是指某序列的前n项和,可以把它理解为数学上的数列的前n项和,而差分可以看成前缀和的逆运算。合理的使用前缀和与差分,可以将某些复杂的问题简单化。
2.前缀和算法有什么好处?
先来了解这样一个问题:
输入一个长度为n的整数序列。接下来再输入m个询问,每个询问输入一对l, r。对于每个询问,输出原序列中从第l个数到第r个数的和。
我们很容易想出暴力解法,遍历区间求和。
代码如下:
> const int N = 1e5 + 10;
> int a[N];
> int n,m;
> scanf("%d%d", &n, &m);
> for(int i = 1; i <= n; i++) scanf("%d", &a[i]); while(m--) {
> int l, r;
> int sum = 0;
> scanf("%d%d", &l, &r);
> for(int i = l; i <= r; i++)
> {
> sum += a[i];
> }
> printf("%d\n",sum); }
这样的时间复杂度为O(n * m),如果n和m的数据量稍微大一点就有可能超时,而我们如果使用前缀和的方法来做的话就能够将时间复杂度降到O(n + m),大大提高了运算效率。
具体做法:
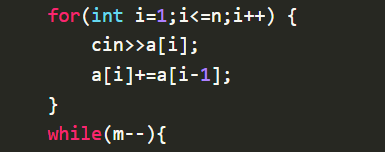](https://i-blog.csdnimg.cn/direct/5b520906254c4dd7af50122a6b9cb917.png)
对于每次查询,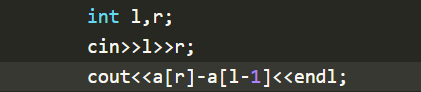
为什么不是a[ r ]-a[ l ]?_
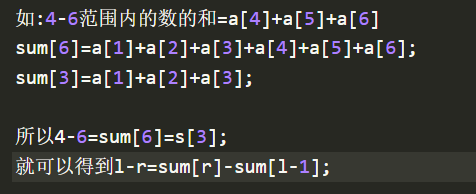
问:最上面的代码不是用a[ i ] 来存累加的和吗 这里怎么又变成sum了?
答:都可以 用a[i]存就不用再定义sum数组,分不清的情况那就定义两个数组,a数组用来存1-n , sum数组存前缀和。




















 691
691

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








