Dijkstra算法详解

今天特意看了Dijkstra算法详解，发现 两篇博客讲得不错，挺透彻的，在此集中一下，方便阅读

【数据结构】有向图（4.dijkstra算法详解）

  (2011-11-01 16:57:19)

转载▼

标签：  数据结构   有向图   dijkstra   最短路径   c   杂谈

分类： 数据结构

    在图的应用中，有一个很重要的需求：我们需要知道从某一个点开始，到其他所有点的最短路径。

    这其中，Dijkstra算法是典型的最短路径算法。它的关键思想是以起始点为中心，向外一层层扩散，直到扩展到终点为止。Dijkstra算法能够得出最短路径的最优解，不过它需要遍历计算的节点相当多，所以效率不高。

 

    首先，用最通俗的语言解释。假定有3个顶点，A、B、C，如图：

    要求A到其余各点的最短路径。很明显，A到C比A到B更短。有疑惑的是从A->B的最短距离，要么是直接A->B的边，要么是A经过C到B的边更短。我们首先找到最短的边（A->C),然后在此基础上扩展，于其余边去对比找到最小值。顶点再进一步扩充增加，按照这个思想，我们总可以找到A到所有点的最短路径。

 

 

算法描述：

    从节点1开始到其余各点的dijkstra算法，其中Wa->b表示边a->b的权，d(i)即为最短路径值，顶点集合为V={1,2,3...n}

    1.置集合S={1}，置顶点集合U={2,3,4...n}，数组d(1)=0,d(i)=W1->i（1，i之间存在边）or 无穷大（1，i之间不存在边）；

 

    2.在U中，令d(j)=min{d(i),i属于U}，将j从U中移至S中，若U为空集则算法结束，否则转3；

 

    3.对全部i属于U，如果存在边j->i,那么置d(i)=min{d(i), d(j) + Wj->i},转2

 

    Dijkstra算法的思想为;设G=(V, E)是一个带权有向图，把图中顶点集合V分为两部分，第一组为已求出最短路径的顶点集合（用S表示，初始时S中只有源点，以后每求出一条最短路径，就将顶点加入到S中，直到所有顶点都加入到S中，算法结束），第二组为其余未求出最短路径的顶点集合（用U表示），按最短路径的长度次序依次将第二组中的顶点加入到第一组中。

 

     在加入过程中，总保持着从源点v到S中各顶点的最短路径不大于从源点v到U中各顶点的最短路径长度。此外，每个顶点对应一个距离，S中的顶点的距离即为源点v到该点的最短路径长度。U中顶点的距离，是从v到此顶点只包括S中的顶点为中间顶点的当前最短距离。

 

 

算法具体步骤

    1.初始时，S中只有源点，即S = {v}，v的距离为0（到自己的距离为0）。U包含除v外地所有其他顶点，U中顶点u距离为边上的权（若v到u存在边）或 ∞ （v到u不存在边，即u不是v的出边邻接点）

 

    2.从U中选取一个距离v最小的顶点k加入到S中（选定的距离就是v到k的最短路径）

 

    3.以k为新考虑的中间点，修改U中各顶点的距离。若从源点v经过顶点k到顶点u的距离比原来距离（不经过顶点k）段，则修改顶点u的距离，修改后的距离值为顶点k的距离加上边k->u的权

 

    4.重复步骤2、3直到所有的顶点都加入到S中

 

 

复杂度分析：

    实现方式的不同，可能有n次或者n-1次外层的循环，这里取n次。

    步骤2每一轮的比较步骤会是n，n-1，n-2...1

    步骤3每一轮的更新步骤会是n-1，n-2...1

    这样计算出结果大致为 n²

    Dijkstra算法的时间复杂度为O(n^2)

    空间复杂度取决于存储方式，邻接矩阵为O(n^2)

 

再看一个例子：

 

 

步骤	S集合中	U集合中
1	选入A，此时S ={A} 此时最短路径A->A = 0 以A为中间点，从A开始找	U = {B, C, D, E, F} A->B = 6 A->C = 3 A->U中其他顶点 = ∞ 其中A->C = 3 权值为最小，路径最短
2	选入上一轮中找到的最短路径的顶点C，此时S = {A, C} 此时最短路径A->A = 0，A->C = 3 以C为中间点，从A->C=3这条最短路径开始新一轮查找	U = {B, D, E, F} A->C->B = 5(比上面的A->B = 6要小) 替换B的权值为更小的A->C->B = 5 A->C->D = 6 A->C->E = 7 A->C->U中其他顶点 = ∞ 其中A->C->B = 5 最短
3	选入B,此时S = {A, C, B} 此时最短路径 A->A = 0，A->C = 3 A->C->B = 5 以B为中间点，从A->C->B = 5这条最短路径开始新一轮查找	U = {D, E, F} A->C->B->D = 10(比上面的A->C->D = 6大，不替换，保持D的权值为A->C->D=6) A->C->B->U中其他顶点 = ∞ 其中 A->C->D = 6 最短
4	选入D,此时 S = {A, C, B, D} 此时最短路径 A->A = 0，A->C = 3，A->C->B = 5，A->C->D = 6 以D为中间点，从A->C->D = 6这条最短路径开始新一轮查找	U = {E, F} A->C->D->E = 8(比上面步骤2中的A->C->E = 7要长，保持E的权值为A->C->E =7) A->C->D->F = 9 其中A->C->E = 7最短
5	选入E,此时 S = {A, C, B, D ,E} 此时最短路径 A->A = 0，A->C = 3，A->C->B = 5，A->C->D = 6，A->C->E =7, 以E为中间点，从A->C->E = 7这条最短路径开始新一轮查找	U = {F} A->C->E->F = 12(比第4步中的A->C->D->F = 9要长，保持F的权值为A->C->D->F = 9) 其中A->C->D->F =9最短
6	选入F,此时 S = {A, C, B, D ,E, F} 此时最短路径 A->A = 0，A->C = 3，A->C->B = 5，A->C->D = 6，A->C->E =7,A->C->D->F = 9	U集合已空，查找完毕

 

算法实现：

伪代码

     Dijkstra算法解决了有向图G=(V, E)上带全的单源最短路径问题，但要求所有的边权非负）。因此，假定每条边(u，v)∈E，有w(u，v)≥0。

 

     Dijksra算法中设置了一个顶点集合S,从源点s到集合中的顶点的最终最短路径的权值均已确定。算法反复选择具有最短路径估计的顶点u∈V-S，并将u加入到S中，对u的所有出边进行松弛。在下面的算法实现中，用到了顶点的最小优先队列Q，排序关键字为顶点的d值。

 

DIJSTRA(G，w，s)

　　1　INITIALIZE-SINGLE-SOURCE(G，s)

　　2　S ← Φ

　　3　Q ← V[G]

　　4　while Q≠Φ

　　5　do u EXTRACT-MIN(Q)

　　6　S ← S∪{u}

　　7　for each vertex v∈Adj[u]

　　8　do RELAX(u，v，w)

C++代码实现

    这是前面代码中复制过来的，仍然是用模板跟容器实现的，可以做些修改使用数组或其他数据结构及实现方式。

 

template<typename vertexNameType, typename weight>
int OLGraph<vertexNameType, weight>::Dijkstra(IN const vertexNameType vertexName1)
{
int sourceIndex = getVertexIndex(vertexName1); //获取源点在容器中索引值
if (-1 == sourceIndex)
{
cerr << "There is no vertex " << endl;
return false;
}
int nVertexNo = getVertexNumber(); //获取顶点数

vector<bool> vecIncludeArray; //顶点是否已求出最短路径
vecIncludeArray.assign(nVertexNo, false); //初始化容器
vecIncludeArray[sourceIndex] = true;

vector<weight> vecDistanceArray; //路径值容器
vecDistanceArray.assign(nVertexNo, weight(INT_MAX)); //将所有顶点到源点的初始路径值为正无穷
vecDistanceArray[sourceIndex] = weight(0); //源点到自己距离置0

vector<int> vecPrevVertex; //路径中，入边弧尾顶点编号（即指向自己那个顶点的编号）
vecPrevVertex.assign(nVertexNo, sourceIndex); //指向所有顶点的弧尾都初始为源点，源点指向所有顶点

getVertexEdgeWeight(sourceIndex, vecDistanceArray); //得到源点到其余每个顶点的距离

int vFrom, vTo;

while(1)
{
weight minWeight = weight(INT_MAX);
vFrom = sourceIndex;
vTo = -1;
for (int i = 0; i < nVertexNo; i++) //找出还没求出最短距离的顶点中，距离最小的一个
{
if (!vecIncludeArray[i] && minWeight > vecDistanceArray[i])
{
minWeight = vecDistanceArray[i];
vFrom = i;
}
}
if (weight(INT_MAX) == minWeight) //若所有顶点都已求出最短路径，跳出循环
{
break;
}
vecIncludeArray[vFrom] = true; //将找出的顶点加入到已求出最短路径的顶点集合中

//更新当前最短路径，只需要更新vFrom顶点的邻接表即可，因为所有vFrom指向的边都在邻接表中
Edge<weight> *p = m_vertexArray[vFrom].firstout;
while (NULL != p)
{
weight wFT = p->edgeWeight;
vTo = p->headvex;
if (!vecIncludeArray[vTo] && vecDistanceArray[vTo] > wFT + vecDistanceArray[vFrom]) //当前顶点还未求出最短路径，并且经由新中间点得路径更短
{
vecDistanceArray[vTo] = wFT + vecDistanceArray[vFrom];
vecPrevVertex[vTo] = vFrom;
}
p = p->tlink;
}

}

for (int i = 0; i < nVertexNo; i++) //输出最短路径
{
if (weight(INT_MAX) != vecDistanceArray[i])
{
cout << getData(sourceIndex) << "->" << getData(i) << ": ";
DijkstraPrint(i, sourceIndex, vecPrevVertex);
cout << " " << vecDistanceArray[i];
cout << endl;
}
}

return 0;
}

template<typename vertexNameType, typename weight>
void OLGraph<vertexNameType, weight>::DijkstraPrint(IN int index, IN int sourceIndex, IN vector<int> vecPreVertex)
{
if (sourceIndex != index)
{
DijkstraPrint(vecPreVertex[index], sourceIndex, vecPreVertex);
}
cout << getData(index) << " ";
}

既然说是最短路，我们当然要有贪心的思想，这里狄克斯特拉完美的做到了这一点。那在算法当中，是如何利用这个贪心思想的呢？我们这里对应一个图来看。（图不咋好看，轻吐槽T T。）

我们假设2是起点，想要走到终点 4，显然我们有两种走法，而且显而易见，走2-> 1-> 4这条路是最短的。我们不希望走2->4这条路。我们通过1这个点，能把从2->4的路径复杂化（多走一步（多转个弯））但是却能够缩短路径耗时的操作，我们理解为松弛操作，我们完成dijkstra的整个算法的过程，无非就是不断的在松弛的过程。我们希望走的路径短，那我们必然要走很多弯路- -*

我们这里对应完整算法的图来理解：

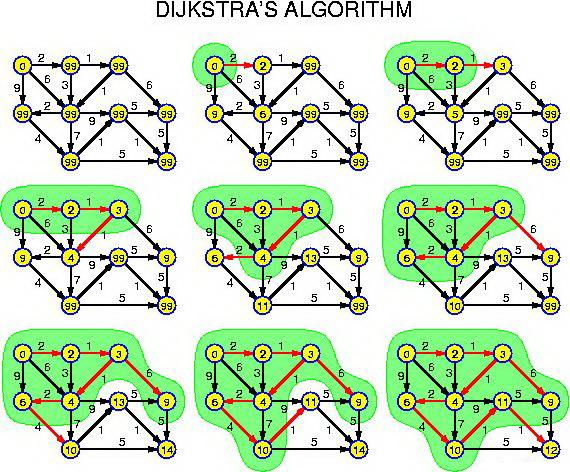
我们这里定义图的编号为：

1 2 3

4 5 6

7 8 9

图1：初始化的图，其中包含边的权值（耗时）。（这里图是有向图）。

图2：确定起点，然后向能直接走到的点走一下，记录此时的估计值：2 6 9.。

图3：找到距离起点最近的点，是正东边的那个点，这时候我们耗费权值为2。然后我们进行松弛操作，从起点到其东南方的点直接到的权值耗费为6，但是我们通过刚刚选定的点，我们找到了到这个点更近的方式，所以这个时候我们说从起点到其东南方向的点的权值更新值从6变成了5。这个时候我们就完成了第一次松弛操作。

图4：依旧是找距离起点最近的点。然后松弛我们发现这个时候从起点到其东南方的点的耗费权值从5又变成了4.这个时候我们完成了第二个松弛。

之后的方式同上：选定距离起点最近的点v。然后通过点v进行松弛操作。我们发现能够通过增加走到目的地方式的复杂度（多转弯）的方式我们能够松弛掉权值，使得耗费的权值更小。

读者请自己跑一遍上边的图，大概的算法思维也就掌握了。

然后我们对应代码和图一起探究：

[cpp]  view plain  copy

 print ?

1. void Dij()//我们这里起点为1号编码点。我们这里的d[]表示从起点到这个点需要的权值。w[a][b]表示点a到点b这条边的权值.  
2. {  
3.     int i,j,k,v,tmp;  
4.     memset(vis,0,sizeof(vis));  
5.     for(i=1;i<=n;i++)  
6.         d[i]=w[1][i];//对应图不难理解，对于起点的初始化  
7.     d[1]=0;  
8.     vis[1]=1;  
9.     for(i=1;i<=n;i++)//控制连接点的次数，例如上图，九个点，就循环九次。  
10.     {  
11.         tmp=N;//这里N表示无穷大。也就是图上的99.  
12.         for(j=1;j<=n;j++)  
13.         {  
14.             if(tmp>d[j]&&!vis[j])  
15.             {  
16.                 tmp=d[j];  
17.                 v=j;  
18.             }  
19.         }//每次我们都找到距离起点最近的点v  
20.         vis[v]=1;  
21.         for(k=1;k<=n;k++)//然后进行松弛操作。<pre name="code" class="cpp">我们这里的d[]表示从起点到这个点需要的权值//加以强调其含义。  

{if(!vis[k])d[k]=min(d[k],d[v]+w[v][k]);}}}

上图为松弛操作的效果图。其中我加了两个蓝色的中途点，表示我们这三个点并不一定是像最初的图那样的三个点，他们其中是有复杂的行进路程的。这样我们就很容易看的出来，是如何进行松弛操作的了~。

对于dijkstra是否能解无向图的问题，这里答案很明确：可以，因为无向图就是特殊的有向图，也可以理解为双向图。这里我们对应HDU的2544进行练习：

最短路

Time Limit: 5000/1000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others)Total Submission(s): 46167    Accepted Submission(s): 20348

Problem Description

在每年的校赛里，所有进入决赛的同学都会获得一件很漂亮的t-shirt。但是每当我们的工作人员把上百件的衣服从商店运回到赛场的时候，却是非常累的！所以现在他们想要寻找最短的从商店到赛场的路线，你可以帮助他们吗？

 

Input

输入包括多组数据。每组数据第一行是两个整数N、M（N<=100，M<=10000），N表示成都的大街上有几个路口，标号为1的路口是商店所在地，标号为N的路口是赛场所在地，M则表示在成都有几条路。N=M=0表示输入结束。接下来M行，每行包括3个整数A，B，C（1<=A,B<=N,1<=C<=1000）,表示在路口A与路口B之间有一条路，我们的工作人员需要C分钟的时间走过这条路。输入保证至少存在1条商店到赛场的路线。

 

Output

对于每组输入，输出一行，表示工作人员从商店走到赛场的最短时间

 

Sample Input

  

   2 1
1 2 3
3 3
1 2 5
2 3 5
3 1 2
0 0
  

 

Sample Output

  

   3
2
  

[cpp]  view plain  copy

 print ?

1. #include<stdio.h>  
2. #include<string.h>  
3. #include<iostream>  
4. using namespace std;  
5. #define N 0x1f1f1f1f  
6. int w[151][151];  
7. int d[155];  
8. int ans,vis[151];  
9. int n,m;  
10. void Dij()  
11. {  
12.     int i,j,k,v,tmp;  
13.     memset(vis,0,sizeof(vis));  
14.     for(i=1;i<=n;i++)  
15.         d[i]=w[1][i];  
16.     d[1]=0;  
17.     vis[1]=1;  
18.     for(i=1;i<=n;i++)  
19.     {  
20.         tmp=N;  
21.         for(j=1;j<=n;j++)  
22.         {  
23.             if(tmp>d[j]&&!vis[j])  
24.             {  
25.                 tmp=d[j];  
26.                 v=j;  
27.             }  
28.         }  
29.         vis[v]=1;  
30.         for(k=1;k<=n;k++)  
31.         {  
32.             if(!vis[k])  
33.             d[k]=min(d[k],d[v]+w[v][k]);  
34.         }  
35.     }  
36. }  
37. int main()  
38. {  
39.     while(~scanf("%d%d",&n,&m))  
40.     {  
41.         if(n==0&&m==0)break;  
42.         for(int i=1;i<=n;i++)  
43.         {  
44.             for(int j=1;j<=n;j++)  
45.             {  
46.                 w[i][j]=0x1f1f1f1f;  
47.             }  
48.         }  
49.         for(int i=0;i<m;i++)  
50.         {  
51.             int a,b,dis;  
52.             scanf("%d%d%d",&a,&b,&dis);  
53.             if(w[a][b]>dis)  
54.             w[a][b]=w[b][a]=dis;  
55.         }  
56.         Dij();  
57.         printf("%d\n",d[n]);  
58.     }